Популярно об ИИ
Сегодня мы побеседуем о такой изначально кажущейся тривиальной вещи, как сортировка. Очень часто можно видеть, что ее учат и преподают, как и тему рекурсии, то есть практически не учат и не преподают :). А в книгах серий "для чайников" и вообще в большинстве книг этому вопросу не уделяется абсолютно никакого внимания, потому как там все направлено на быстрый эффект.
Получается интересная вещь: люди могут собирать сложные структуры баз данных, используют многопоточность и т.п., но сортировка, управление очередями, стеками, массивами данных для них является чем-то архисложным. Многие поспорят со сказанным, но могу спросить, вы видели, как используется сортировка, когда программа подвисает? Скажем, в рамках плохо отлаженных разработок нередко. Все уже привыкли к высокоуровневым моделям, и в ряде случаев люди используют заранее подготовленные методы, хотя их внутреннюю структуру представляют с трудом. Между тем принципы сортировки нужно знать, особенно программистам ИИ.
Вообще, жизнь показывает интересные вещи. В середине 90-х, когда я выполнял заказы, то хранил базы данных в текстовых файлах (с символьными разделителями или без оных), а управление этой структуры реализовывалось за счет функций того или иного языка. Потом я внимательно посмотрел на HTML, и решил, что html-теги весьма удобно использовать в качестве символьных разделителей. И только через несколько лет появился такой стандарт, как XML. То есть мысли сошлись, и получается, что я в свое время разработал и использовал технологию будущего. Сейчас я храню базы данных в подгружаемых исполняемых Lua-файлах, в коих содержатся не только сами данные, но и все методы, которые можно к ним применить, а также взаимосвязываются структуры. Их наполнение можно менять динамически.
Создать свою собственную структуру базы данных и реализовать систему управления ею вообще несложно на самом деле, но пользователи-программисты привыкли тратить много времени на изучение и использование уже готовых технологий.
В общем, сейчас мы рассмотрим некоторые базовые постулаты. Как хорошую книгу для прочтения рекомендуем: Арт Фридман, Ларс Кландер, Марк Михаэлис, Херб Шильдт "С/С++. Архив программ", издательство "Бином", 2001 г. В зарубежной прессе данная серия книг идет с подзаголовком Annotated Archives.
Поговорим о сортировке. Разработано много алгоритмических моделей, то есть тема достаточно хорошо изучена, но стоит отметить тот момент, что нужно знать базовые принципы, а в каждом отдельном случае той же сортировкой можно управлять.
Масштаб
Перед тем как решать вопросы сортировки, необходимо знать объем данных, которые необходимо обрабатывать. Есть методы, которые наиболее эффективны при малом количестве элементов, но они становятся довольно громоздкими при большом. Также есть и специальные методы, один из которых мы рассмотрим в конце материала.
Простой метод — пузырьковая сортировка
Название этого метода описательное, то есть подразумевается всплывающий на поверхность воды пузырек воздуха. В принципе, это хорошее и понятное сравнение.
Представьте себе целочисленный массив, состоящий, например, из пяти элементов. Вам нужно расставить их в порядке возрастания значений чисел, то есть data[0] будет содержать минимальное число, а data[4] — максимальное из имеющихся. Что происходит в рамках этого алгоритма. Изначально, верхний элемент data[4] сравнивается с предыдущим data[3], и если его значение меньше, элементы меняются местами. И так далее, пока минимальный элемент не всплывет как пузырек воздуха. Фактически, все сказанное будет проще описать кодом:
for (i=0, i<size-1;i++) {
for (j=size-1, j>i;--i) {
if (array[i-1]>array[j]) swap(array,i-1,j);
}
}
size — эта величина массива, но в рамках цикла мы берем значение size-1 поскольку максимальный элемент автоматически занимает свою позицию. Внутренний цикл for проходит в обратном по отношению к внешнему направлении, хотя можно делать и в прямом.
Метод пузырьковой сортировки имеет один недостаток — большое количество действий, то есть он ресурсоемкий. При этом, проанализировав, вы можете сказать, в чем заключается основная проблема — перемещение элементов всего на одну позицию.
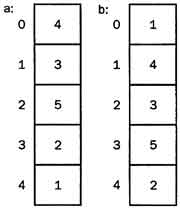Пузырьковая сортировка. a — изначальный массив; b — четвертый элемент "всплывает" на поверхность
Простой метод — выборочная сортировка
А можно ли сделать так, чтобы элемент сравнивался со всеми имеющимися, и при удовлетворении условий становился на позицию data[0], совершая только единственный обмен? Да, именно так работает выборочная сортировка. Она является усовершенствованным вариантом пузырьковой. То есть, изначально из всего массива отыскивается минимальное значение, определяется его индекс. После этого меняются местами data[0] и data[индекс минимального значения]. Потом берется следующий подмассив, в котором уже не учитывается data[0], и мы заполняем минимальным значением data[1] и так далее.
В коде это писать немного объемно (за что часто ругают журналистов ИТ-СМИ:)), поэтому скажем, что нам понадобится один внутренний цикл, в котором мы находим значение индекса элемента, содержащего минимальное число, а после делаем перестановку. Потом производим такой же поиск в подмассиве и так далее, что делается во внешнем цикле. При этом код оптимизируется ограничением того, что перестановка производится в случае, если переставляемый элемент не содержит минимальное значение, то есть if (min_index != i) {swap…}.
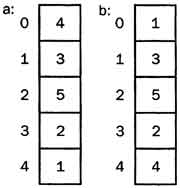Выборочная сортировка. Здесь показано, как последний элемент массива меняется местами с первым
Сложный метод — быстрая сортировка
Быстрая сортировка является одним из самых эффективных методов, а по существу это две взаимосвязанных сортировки. Суть метода заключается в том, что из массива выбирается какой-либо элемент, который будет выступать в качестве разделяющего значения. Разделяющего(!) — это значит, что оно будет разделять. А что именно? На самом деле, подразумевается двухсторонне движение от начала массива и его конца, по терминологии проще применять названия Head (голова) и Tail (хвост). То есть, если мы говорим о расстановке чисел по возрастанию, алгоритм сортировки в Head будет сравнивать числа на условие > разделяющего значения (если "да", то это большое значение меняется с разделяющим), а алгоритм сортировки в Tail будет сравнивать числа на условие <разделяющего значения (если "да", то это большое значение меняется с разделяющим). В момент, когда Head и Tail сходится на одном элементе (место пересечения указателей), мы можем сказать, что все что справа (или ниже) меньше разделяющего значения, а все, что слева (сверху) — больше.
Потом эти две части сортируются по отдельности таким же образом (функция сортировки рекурсивно вызывает саму себя).
Быстрый алгоритм часто сопровождают фразой: "разделяй и властвуй". Это так, но очень многое зависит от выбора разделяющего элемента/значения. Например, массив, содержащий -3,5,0,7,2. Попробуйте сами выбрать значение, которое обеспечит максимально быструю сортировку (наиболее удобным вариантом при первом цикле сортировки окажется 0 или 2) и наиболее медленную (когда для первого цикла сортировки вы выберите в качестве разделяющего максимальное или минимальное значение, т.е. -3 или 7). Наиболее выгодной ситуацией также будет, когда массив делится на две равные части.
Внимательно присмотревшись, вы также обнаружите, что в ряде случаев быстрая сортировка не выигрывает по сравнению с простыми методами, о которых мы написали. А самый большой минус будет в случае, когда мы применим быструю сортировку к уже отсортированному массиву.
Вообще, методов быстрой сортировки существует несколько, их основное отличие состоит в алгоритме выбора разделяющего значения (процедуре разбиения), оптимизации рекурсии.
У быстрой сортировки есть и еще один веселый минус — вхождение в бесконечность. То есть, массив 3,2,3 приведет к критической ситуации, потому как нужна процедура обработки повторяющихся значений, чего в стандартных алгоритмах не предусмотрено.
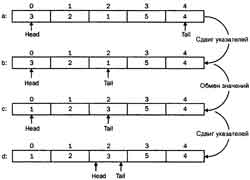Быстрая сортировка. В качестве разделяющего значения выбрано 3 (крайнее левое значение). Tail, дойдя до единицы (b), сталкивается с условием "текущее значение < разделяющего", происходит обмен. Потом идет проверка со стороны Head, так как ситуация изменилась, указатели пересекаются на элементе массива a[2]. Следующим этапом будет идентичная обработка правой и левой частей
Сложный метод — улучшенная быстрая сортировка
Улучшенная быстрая сортировка более точно подходит к выбору значения разделения. Нужно определиться с медианой массива, то есть серединным значением в общем спектре. Ее определение достаточно затратно, но чем большее количество значений нужно обрабатывать, тем лучше получается баланс затрачиваемых ресурсов.
Для определения медианы обычно находится среднее значение между двумя крайними и серединным элементами. Для решения ситуации с повторяющимися значениями предусмотрена специальная процедура, использующая конструкции if (…<=… или …>=…) либо же просто обыгрывается ситуация в случае возникновении равенства.
Сложный метод — сортировка слиянием
Сортировка слиянием подразумевает функцию сортировки с разбиением массива пополам — на два подмассива, после функция сортировки вызывает себя рекурсивно для каждой из половин, после чего объединяет сортированные подмассивы в один массив. Вся работа по сортировке производится по мере разматывания стека вызовов. Для функционирования алгоритма нужен дополнительный временный массив того же размера, что и исходный, который после копируется в основной.
Сортировка слиянием лучше улучшенной быстрой сортировки в силу простоты (не нужно никаких разделяющих элементов и скрещивания указателей), а также в ней не возникает проблемы наихудшего случая, который может появиться при быстрой сортировке.
Сложный метод — "дискретная сортировка"
На моей памяти я его встречал только несколько раз. Впрочем, он однажды мне понадобился, поэтому я таковой разработал и сам. По существу, данный алгоритм работает как… АЦП и несколько других известных алгоритмов. То есть, изначально в массиве ищется максимальное и минимальное значения. Потом вычисляется среднее из них, то есть диапазон значений/2. После этого все элементы проходят сравнение с этим значением, и те, что меньше, заносятся в левую часть, те, что больше — в правую. Создается временный массив таких же размеров, что и исходный, в котором элементы, которые помещаются слева, получают индексы, начиная с нуля, а те, которые слева — с [общее кол-во эл-тов – текущий индекс для правой части]. Затем (для каждой из половин мы уже знаем их средние значения 1/4 диапазона и 3/4 диапазона значений, а также количество элементов в каждой из половин), мы также производим сравнения со средними значениями половин и так далее, пока не доходим до одного элемента. После этого идет сборка с соответствующей расстановкой индексов. "Дискретная сортировка" как и сортировка слиянием, требует наличия дополнительного массива, то есть, как говорится, выполняется не "по месту".
Не сказать, что алгоритм дискретной сортировки трудоемок в исполнении, хотя есть и сложные варианты исполнения. Он надежен, но достаточно ресурсоемок. Хорошо применим для случаев неоднородных массивов, в которых присутствуют "пустоты", то есть, например, диапазон значений от 0 до 100, а основная масса значений элементов сосредоточена в интервале 80-90. А вообще, основная прелесть дискретной сортировки и ее методов проявляется в случаях, когда нужно округлять значения, отслеживать определенные участки динамически пополняемых массивов и так далее.
В завершение
Как видите, особенно сложного в рамках сортировки ничего придумано не было. Нужно только внимательно присмотреться. Сами алгоритмы достаточно хорошо облегчаются в условиях, когда вы хорошо разбираетесь во внутренней структуре задачи. Например, если в общем случае тот или иной алгоритм описывается как ресурсоемкий и располагающий к ошибкам, то в частном он может быть наиболее эффективным при правильной расстановке ограничений. В следующей части материала мы поговорим о стеке и рекурсии, оптимизации рекурсии.
Кристофер christopher@tut.by
Получается интересная вещь: люди могут собирать сложные структуры баз данных, используют многопоточность и т.п., но сортировка, управление очередями, стеками, массивами данных для них является чем-то архисложным. Многие поспорят со сказанным, но могу спросить, вы видели, как используется сортировка, когда программа подвисает? Скажем, в рамках плохо отлаженных разработок нередко. Все уже привыкли к высокоуровневым моделям, и в ряде случаев люди используют заранее подготовленные методы, хотя их внутреннюю структуру представляют с трудом. Между тем принципы сортировки нужно знать, особенно программистам ИИ.
Вообще, жизнь показывает интересные вещи. В середине 90-х, когда я выполнял заказы, то хранил базы данных в текстовых файлах (с символьными разделителями или без оных), а управление этой структуры реализовывалось за счет функций того или иного языка. Потом я внимательно посмотрел на HTML, и решил, что html-теги весьма удобно использовать в качестве символьных разделителей. И только через несколько лет появился такой стандарт, как XML. То есть мысли сошлись, и получается, что я в свое время разработал и использовал технологию будущего. Сейчас я храню базы данных в подгружаемых исполняемых Lua-файлах, в коих содержатся не только сами данные, но и все методы, которые можно к ним применить, а также взаимосвязываются структуры. Их наполнение можно менять динамически.
Создать свою собственную структуру базы данных и реализовать систему управления ею вообще несложно на самом деле, но пользователи-программисты привыкли тратить много времени на изучение и использование уже готовых технологий.
В общем, сейчас мы рассмотрим некоторые базовые постулаты. Как хорошую книгу для прочтения рекомендуем: Арт Фридман, Ларс Кландер, Марк Михаэлис, Херб Шильдт "С/С++. Архив программ", издательство "Бином", 2001 г. В зарубежной прессе данная серия книг идет с подзаголовком Annotated Archives.
Поговорим о сортировке. Разработано много алгоритмических моделей, то есть тема достаточно хорошо изучена, но стоит отметить тот момент, что нужно знать базовые принципы, а в каждом отдельном случае той же сортировкой можно управлять.
Масштаб
Перед тем как решать вопросы сортировки, необходимо знать объем данных, которые необходимо обрабатывать. Есть методы, которые наиболее эффективны при малом количестве элементов, но они становятся довольно громоздкими при большом. Также есть и специальные методы, один из которых мы рассмотрим в конце материала.
Простой метод — пузырьковая сортировка
Название этого метода описательное, то есть подразумевается всплывающий на поверхность воды пузырек воздуха. В принципе, это хорошее и понятное сравнение.
Представьте себе целочисленный массив, состоящий, например, из пяти элементов. Вам нужно расставить их в порядке возрастания значений чисел, то есть data[0] будет содержать минимальное число, а data[4] — максимальное из имеющихся. Что происходит в рамках этого алгоритма. Изначально, верхний элемент data[4] сравнивается с предыдущим data[3], и если его значение меньше, элементы меняются местами. И так далее, пока минимальный элемент не всплывет как пузырек воздуха. Фактически, все сказанное будет проще описать кодом:
for (i=0, i<size-1;i++) {
for (j=size-1, j>i;--i) {
if (array[i-1]>array[j]) swap(array,i-1,j);
}
}
size — эта величина массива, но в рамках цикла мы берем значение size-1 поскольку максимальный элемент автоматически занимает свою позицию. Внутренний цикл for проходит в обратном по отношению к внешнему направлении, хотя можно делать и в прямом.
Метод пузырьковой сортировки имеет один недостаток — большое количество действий, то есть он ресурсоемкий. При этом, проанализировав, вы можете сказать, в чем заключается основная проблема — перемещение элементов всего на одну позицию.
Простой метод — выборочная сортировка
А можно ли сделать так, чтобы элемент сравнивался со всеми имеющимися, и при удовлетворении условий становился на позицию data[0], совершая только единственный обмен? Да, именно так работает выборочная сортировка. Она является усовершенствованным вариантом пузырьковой. То есть, изначально из всего массива отыскивается минимальное значение, определяется его индекс. После этого меняются местами data[0] и data[индекс минимального значения]. Потом берется следующий подмассив, в котором уже не учитывается data[0], и мы заполняем минимальным значением data[1] и так далее.
В коде это писать немного объемно (за что часто ругают журналистов ИТ-СМИ:)), поэтому скажем, что нам понадобится один внутренний цикл, в котором мы находим значение индекса элемента, содержащего минимальное число, а после делаем перестановку. Потом производим такой же поиск в подмассиве и так далее, что делается во внешнем цикле. При этом код оптимизируется ограничением того, что перестановка производится в случае, если переставляемый элемент не содержит минимальное значение, то есть if (min_index != i) {swap…}.
Сложный метод — быстрая сортировка
Быстрая сортировка является одним из самых эффективных методов, а по существу это две взаимосвязанных сортировки. Суть метода заключается в том, что из массива выбирается какой-либо элемент, который будет выступать в качестве разделяющего значения. Разделяющего(!) — это значит, что оно будет разделять. А что именно? На самом деле, подразумевается двухсторонне движение от начала массива и его конца, по терминологии проще применять названия Head (голова) и Tail (хвост). То есть, если мы говорим о расстановке чисел по возрастанию, алгоритм сортировки в Head будет сравнивать числа на условие > разделяющего значения (если "да", то это большое значение меняется с разделяющим), а алгоритм сортировки в Tail будет сравнивать числа на условие <разделяющего значения (если "да", то это большое значение меняется с разделяющим). В момент, когда Head и Tail сходится на одном элементе (место пересечения указателей), мы можем сказать, что все что справа (или ниже) меньше разделяющего значения, а все, что слева (сверху) — больше.
Потом эти две части сортируются по отдельности таким же образом (функция сортировки рекурсивно вызывает саму себя).
Быстрый алгоритм часто сопровождают фразой: "разделяй и властвуй". Это так, но очень многое зависит от выбора разделяющего элемента/значения. Например, массив, содержащий -3,5,0,7,2. Попробуйте сами выбрать значение, которое обеспечит максимально быструю сортировку (наиболее удобным вариантом при первом цикле сортировки окажется 0 или 2) и наиболее медленную (когда для первого цикла сортировки вы выберите в качестве разделяющего максимальное или минимальное значение, т.е. -3 или 7). Наиболее выгодной ситуацией также будет, когда массив делится на две равные части.
Внимательно присмотревшись, вы также обнаружите, что в ряде случаев быстрая сортировка не выигрывает по сравнению с простыми методами, о которых мы написали. А самый большой минус будет в случае, когда мы применим быструю сортировку к уже отсортированному массиву.
Вообще, методов быстрой сортировки существует несколько, их основное отличие состоит в алгоритме выбора разделяющего значения (процедуре разбиения), оптимизации рекурсии.
У быстрой сортировки есть и еще один веселый минус — вхождение в бесконечность. То есть, массив 3,2,3 приведет к критической ситуации, потому как нужна процедура обработки повторяющихся значений, чего в стандартных алгоритмах не предусмотрено.
Сложный метод — улучшенная быстрая сортировка
Улучшенная быстрая сортировка более точно подходит к выбору значения разделения. Нужно определиться с медианой массива, то есть серединным значением в общем спектре. Ее определение достаточно затратно, но чем большее количество значений нужно обрабатывать, тем лучше получается баланс затрачиваемых ресурсов.
Для определения медианы обычно находится среднее значение между двумя крайними и серединным элементами. Для решения ситуации с повторяющимися значениями предусмотрена специальная процедура, использующая конструкции if (…<=… или …>=…) либо же просто обыгрывается ситуация в случае возникновении равенства.
Сложный метод — сортировка слиянием
Сортировка слиянием подразумевает функцию сортировки с разбиением массива пополам — на два подмассива, после функция сортировки вызывает себя рекурсивно для каждой из половин, после чего объединяет сортированные подмассивы в один массив. Вся работа по сортировке производится по мере разматывания стека вызовов. Для функционирования алгоритма нужен дополнительный временный массив того же размера, что и исходный, который после копируется в основной.
Сортировка слиянием лучше улучшенной быстрой сортировки в силу простоты (не нужно никаких разделяющих элементов и скрещивания указателей), а также в ней не возникает проблемы наихудшего случая, который может появиться при быстрой сортировке.
Сложный метод — "дискретная сортировка"
На моей памяти я его встречал только несколько раз. Впрочем, он однажды мне понадобился, поэтому я таковой разработал и сам. По существу, данный алгоритм работает как… АЦП и несколько других известных алгоритмов. То есть, изначально в массиве ищется максимальное и минимальное значения. Потом вычисляется среднее из них, то есть диапазон значений/2. После этого все элементы проходят сравнение с этим значением, и те, что меньше, заносятся в левую часть, те, что больше — в правую. Создается временный массив таких же размеров, что и исходный, в котором элементы, которые помещаются слева, получают индексы, начиная с нуля, а те, которые слева — с [общее кол-во эл-тов – текущий индекс для правой части]. Затем (для каждой из половин мы уже знаем их средние значения 1/4 диапазона и 3/4 диапазона значений, а также количество элементов в каждой из половин), мы также производим сравнения со средними значениями половин и так далее, пока не доходим до одного элемента. После этого идет сборка с соответствующей расстановкой индексов. "Дискретная сортировка" как и сортировка слиянием, требует наличия дополнительного массива, то есть, как говорится, выполняется не "по месту".
Не сказать, что алгоритм дискретной сортировки трудоемок в исполнении, хотя есть и сложные варианты исполнения. Он надежен, но достаточно ресурсоемок. Хорошо применим для случаев неоднородных массивов, в которых присутствуют "пустоты", то есть, например, диапазон значений от 0 до 100, а основная масса значений элементов сосредоточена в интервале 80-90. А вообще, основная прелесть дискретной сортировки и ее методов проявляется в случаях, когда нужно округлять значения, отслеживать определенные участки динамически пополняемых массивов и так далее.
В завершение
Как видите, особенно сложного в рамках сортировки ничего придумано не было. Нужно только внимательно присмотреться. Сами алгоритмы достаточно хорошо облегчаются в условиях, когда вы хорошо разбираетесь во внутренней структуре задачи. Например, если в общем случае тот или иной алгоритм описывается как ресурсоемкий и располагающий к ошибкам, то в частном он может быть наиболее эффективным при правильной расстановке ограничений. В следующей части материала мы поговорим о стеке и рекурсии, оптимизации рекурсии.
Кристофер christopher@tut.by
Компьютерная газета. Статья была опубликована в номере 20 за 2009 год в рубрике технологии
