Популярно об ИИ
"Мой метод заключается в том, чтобы найти какую-нибудь хорошую мысль и предположить, что она истинна".
Билл Джой (Bill Joy)
Мировой финансовый кризис весьма интересен с математической точки зрения. Тут, конечно, явно напрашивается сравнение с психоисторией, предложенной в рамках фантастической трилогии с "Основаниями" Айзека Азимова, но и не только с ней. Играя в экономические стратегии (компьютерные игры), вы сталкиваетесь в большинстве случаев с тривиальнейшими экономическими моделями, которые построены по учебникам. Они являются частными случаями, но не более того. Причем с такими же моделями мы встречаемся и в жизни (если кто-то испугался сравнения с играми). Сегодня поговорим о том, что 2+2, кроме как в буквальном арифметическом смысле, не равно 4-м. Для этого немного попрограммируем, а те, кто не хотят, могут просто посмотреть на результаты, хотя предложенные примеры дадут волю фантазии экспериментаторам. После мы разовьем идею дальше.
Муар
В данном случае мы не будем говорить конкретно о технологии иллюзий, потому как результат оказывается очевидным и к разделу иллюзий как таковых его можно отнести с натяжкой.
Приведенный пример ваш покорный слуга решил показать на уровне Visual С#, причем с объяснением программирования, чтобы не столкнуться с такой же ситуацией, которая сложилась после публикации материала с дисками Бенхама, когда завалили тривиальными вопросами. Такой выбор языка сделан неспроста, поскольку он понятен большей части программистов, работающих на других схожих (С++, Java, Visual Basic и т.п.), является современным, перспективным и распространенным. Хотя нас пугают, что в Visual Studio 2010 он будет совмещен с Visual Basic (как говорят китайцы: "Чтоб ты жил в эпоху перемен"), C# очень удобен. На ActionScript также дадим небольшой идентичный листинг.
Задание — муар
Нам нужно создать и отобразить на форме два зеркальных и пересекающихся между собой массива отрезков. При этом в каждом из них эти самые отрезки не параллельны, а имеют небольшой и постоянный угол отклонения по отношению друг к другу.
Реализация
Итак, запускаем Visual C#, создаем новый проект Windows Application, назовем его Muar, нажимаем ОК, появляется чистая форма. В окне свойств этой формы мы меняем имя шапки на "Муар" (поле "Text"), устанавливаем размеры окна 500х500 (поле "Size"), вы можете предусмотреть свои варианты. Фоновым цветом окна формы (поле "Back Color") для лучшего восприятия устанавливаем белый. Все первоначальные настройки произведены, теперь в окне свойств переключаемся на события (Events, до этого мы были в закладке Properties), делаем двойной клик на строке Paint, в результате чего открывается окно с кодом для файла Form1.cs, и в появившейся нише записываем следующее:
private void Form1_Paint(object sender, PaintEventArgs e)
{
//малый и большой
//шаги, начальные
//координаты по Y
int h1 = 4, h2 = 6, y1 = 50, y2 =0;
//задаем цвет и
//толщину пера
Pen myPen = new Pen(Color.Black, 1);
//запускаем цикл на 79 итераций
for (; y1 < 371; y1 += h1)
{
y2 += h2;
//рисуем первые линии
e.Graphics.DrawLine(myPen, 20, y1, 480, y2);
//рисуем вторые линии
e.Graphics.DrawLine(myPen, 20, y2, 480, y1);
}
//Высвобождаем память,
//выделенную объекту myPen
myPen.Dispose();
}
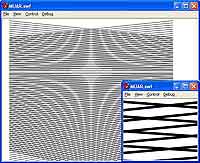
Все! Программа готова. Build -> Build Solution (или Ctrl+Shift+B), Debug -> Start Without Debugging (или Ctrl+F5), появилось окно с пересекающимися прямыми линиями. Но данное пересечение дает интересный эффект — мы отчетливо видим сложный рисунок, который и называется муаром. Точно такой же эффект можно наблюдать при сложении складок тюлевых занавесок на окне.
 Наша программа, написанная на Visual C#. 1 — выводится только один массив отрезков; 2 — два зеркальных массива пересекаются и дают муар; 3 — пересекающиеся массивы состоят из параллельных отрезков; 4 — пересечение первого массива с массивом дугообразных линий.
Наша программа, написанная на Visual C#. 1 — выводится только один массив отрезков; 2 — два зеркальных массива пересекаются и дают муар; 3 — пересекающиеся массивы состоят из параллельных отрезков; 4 — пересечение первого массива с массивом дугообразных линий.
Теперь рассмотрим пример более подробно, причем обратим внимание и на представленный рисунок с четырьмя изображениями. Итак, некая нелинейность у нас имеет место в силу того, что массив отрезков сужается с одной стороны. Сами линии мы рисуем, просто указывая координаты двух конечных точек, при этом в правой части они формируются с одним шагом, в левой — с другим. В принципе, муар уже появляется даже при прорисовке только первого массива отрезков (что показано на изображении 1) в силу того, что мы имеем компьютерный попиксельный вариант рисования без продуктивного сглаживания. То есть резкие изломы сами по себе уже формируют новые линии. В природе, как вы понимаете, такого не наблюдается.
При наложении друг на друга двух зеркальных массивов отрезков (что показано на изображении 2) мы отчетливо видим рисунок, появившийся в результате их взаимодействия. Он носит явно нелинейный характер. При этом, если мы захотим сделать вариант пересечения параллельных линий, то есть приравняв шаги формирования вершин с двух сторон, то получим результат в виде вертикальных полос (что показано на изображении 3) и при удалении точки просмотра — горизонтальных градиентов. А на изображении 4 вместо второго массива отрезков прямых линий мы вставили множество дуг, заменив внутри цикла соответствующую строку кода на:
e.Graphics.DrawArc(myPen, 20, y2, 450, 10, 180, -180);
Листинг я вам дал и для того, чтобы вы смогли начать экспериментировать. На самом деле можно добиться великолепных эффектов, и высшим пилотажем в этом деле является получение видимых изображений, текста, разноплановых узоров и так далее. Да и сам вариант нелинейного перетекания форм заслуживает восхищения математического и эстетического толка.
Поскольку отсутствие продуктивного сглаживания может многим не понравиться, к тому же данный программный код применим не для всех языков, позволим себе дать небольшой листинг такой же программы на флеше (ActionScript 2), который сейчас изучают школьники, и правильно делают. В этой среде немного другой способ рисования, причем один из самых эффективных методов сглаживания линий, который стоит на автомате. Итак, открываем Adobe Flash, выбираем создание проекта ActionScript 2.0, делаем активным окно Actions, при этом нажимаем указателем мыши на "кирпичике" первого кадра Layer 1. Когда будем вводить код, на этом "кирпичике" автоматически появится значок альфы.
Итак, что же мы вводим (даем без комментариев, и так все понятно):
this.createEmptyMovieClip("MUAR_mc",1);
i = 0;
h1 = 4;
h2 = 6;
y1 = 50;
y2 = 0;
with (MUAR_mc) {
lineStyle(1,0x000000,100);
while (i<80) {
y1 += h1;
y2 += h2;
moveTo(20,y1);
lineTo(480,y2);
moveTo(20,y2);
lineTo(480,y1);
i++;
}
}
Запускаем Debug, видим изображение.
 Реализация программы во флеше. На самом деле, находясь в мелком масштабе, мы не можем оценить то, как выглядит общая структура.
Реализация программы во флеше. На самом деле, находясь в мелком масштабе, мы не можем оценить то, как выглядит общая структура.
Некоторые выводы
Почему в данном случае мы можем говорить, что 2+2 не равно 4-м?
Если мы берем какой-то частный случай и начинаем его рассматривать при уменьшенном масштабе, то очень редко можно догадаться, что он является фрагментом какой-то большей взаимосвязанной структуры.
Математики очень любят подобные эксперименты в силу того, что из двух простейших элементов возникает нечто сложное.
И действительно, в нашем примере мы сложили 79 линий плюс 79, но в результате при визуальном восприятии получили не 158, а гораздо больше. Так вот, если мы сильно уменьшим масштаб до того, чтобы видеть только, как две линии пересекаются с двумя, то будем думать, что общей их суммой является 4, то есть мы увидим просто 4 линии… При отдалении просмотра картина меняется. Отсюда можно сделать вывод, что обычная арифметика актуальна только для строго определенного масштаба.
Мало того, при сильном укрупнении масштаба вся картина превратится в совокупность кривых, а прямые отрезки, которых мы уже не сможем детализировать, становятся не видными. То есть, при близком просмотре результат один, при удаленном — абсолютно другой и неожиданный. Есть и еще одна тематическая параллель, для чего обратимся к интереснейшей истории.
Гаусс, Гаусс…
Бесспорно, Карл Фридрих Гаусс был великим математиком, но существовал один прецедент, за который некоторые ученые его недолюбливали, хотя и признавали заслуги. Речь идет о неевклидовой геометрии. Пятый постулат Евклида говорит, что параллельные линии никогда не пересекаются и как следствие сумма углов треугольника равна 180 градусов. Согласитесь, такой математике нас до сих пор учат в школе. Но вы можете нарисовать треугольник, например, на сфере, либо просто представить его на глобусе как два меридиана, пересекающие экватор, но при этом сходящиеся на полюсах. То есть, у экватора само пересечение идет под прямыми углами (т.е. 90 и 90, и мы уже получаем 180), но есть и еще один угол у полюса. Также есть и примеры с получением суммы углов меньшей, чем 180 градусов, то есть треугольник нужно поместить на поверхности с отрицательной кривизной (для наглядности представьте себе фрагмент песочных часов). Так вот, Гаусс это нашел, проработал, был способен решать задачи "в этой геометрии", но не захотел не только публиковать результаты своих исследований, но и просил своих друзей держать все в тайне. Карла Фридриха считали королем математики, и он в действительности мог уже тогда сделать революцию, но перестраховывался.
Однажды Гаусса попросили составить карту Ганноверского королевства. В принципе, это была задача абсолютно не его уровня, но многие думают, что математик взялся за это, поскольку собирался проверить свои догадки. Он соорудил особо точный прибор, измерения проводились с немецкой дотошностью, и (как опять же предполагают многие) Гаусс хотел проверить измерения углов больших пространственных треугольников и получить сумму не равную 180 градусам. Но… ему это не удалось. С одной стороны, Ганноверское королевство слишком мало в рамках неевклидовой геометрии применительно к земному шару, хотя интересно в данном случае то, что если бы у него была просто большая сфера и точные приборы, то, наверное, и карту не пришлось бы составлять. То есть не очень верится, что Гаусс бы до такого не додумался, а принялся измерять земной шар. С другой стороны, есть теоретические изыскания, а есть и практическая применимость. Измерив Ганноверское королевство, Гаусс убедился, что для практики все не имеет большого значения.
Чего боялся ученый? В некоторых его письмах друзьям были строки о том, что если он только заикнется об этой теме, его поднимут на смех. Но тут стоит напомнить о практическом смысле нововведений, который выглядел туманным.
В то же время, когда Гаусс "измерял" королевство, в 1826 г. в Казани Николай Лобачевский пытался прочитать на заседании университетского совета лекцию о "воображаемой геометрии" и был осмеян, даже до конца не дочитал. Но он публиковался, активно продвигая свою идею, несмотря на сопротивление. Причем Гаусс, увидев его труды в 1840 году в немецкой научной прессе, пришел в большое волнение, он поспособствовал принятию Лобачевского в члены-корреспонденты Геттингенской академии наук. Но… ничего не сделал, то есть не объявил неевклидову геометрию правильной, чего от него Лобачевский ждал. Гаусс даже начал изучать русский для того, чтобы прочитать все работы Николая Ивановича, но делал это скрытно, не перекинувшись с русским ученым даже одним словом.
Над тем смеялись, хотя одного сказанного во всеуслышание мнения Гаусса было бы достаточно для того, чтобы эту математику приняли. Не менее интересно ситуация развернулось с Яношем Бойаи — сыном друга Карла Фридриха. Тот написал свой труд о неевклидовой геометрии, когда ему еще не было 20-ти. Работу отослали Гауссу для рассмотрения. Ответ пришел через долгое время, в нем Гаусс сообщал, что сделал это открытие 30 лет назад и… все. Наверное, нужно пояснить некоторую специфику того времени. Гаусс был математиком номер один, он мог признать или не признать определенное направление, от его воли зависело практически все. Но он этого не сделал и в этот раз. Бойаи ждал признания хоть не себя, но хотя бы научной правды до самой смерти, в конце жизни он стал душевнобольным. Причем, что удивительно, до всего в плане неевклидовой геометрии додумался сам.
Но веселее всего обстояло дело с Бернхардом Риманом. Тот сначала защитил диссертацию в Геттингенском университете, причем восхитив тогда самого Гаусса. Потом стал искать работу, и для того чтобы получить одну из должностей, нужно было прочитать пробную лекцию. Ученый предложил три темы, а Гаусс, которому уже было 75 лет, выбрал себе на горе либо из спортивного интереса "основы геометрии".
Это было восхитительно. До сих пор Римана по праву считают одним из самых великих ученых, если не самым великим. А тогда, в отличие от того же Лобачевского и Боайи, которые отвергали пятый постулат, Бернхард Риман просто отверг всего Евклида, показав, что существует множество классов неевклидовых геометрий. Мало того, все держалось на его (Римана) собственных принципах, а многое было представлено без доказательств. Математики были в шоке, Гаусс молча вышел, от его друзей потом стало известно, что он пришел в "высочайшее изумление".
Итак, а теперь откроем "Советскую энциклопедию", ищем… Риман… Бернхард… Читаем: "Риманова геометрия… Изучает свойства многомерных пространств, в малых областях которых имеет место (с точностью до бесконечно малых второго порядка) евклидова геометрия (при этом все пространство может не быть евклидовым)". Конечно, ваш покорный слуга мог бы многое рассказать вам о Римане и без "Советской Энциклопедии", но тут и так все понятно. И странное дело, Лобачевский в своей теории все разложил по полочкам с доказательствами и так далее, но над ним смеялись и издевались (как показывают некоторые исторические заметки), Бойаи сошел от безысходности с ума, Гаусс боялся, что его, величайшего, вдруг поднимут на смех. А Риман злил всех и вся, доказательств минимум, реакция ученых не задевает, и если все ждали от Гаусса признания, то Бенхарда Римана оно вообще не сильно волновало.
А в общем и целом, если нас сейчас читают начинающие математики, то им следует присмотреться к Риману, потому как недоказанного и очень интересного у него осталось достаточно много.
А обычный читатель уже понял, к чему был этот рассказ, то есть, в рамках определенного масштаба и представленного определенным же образом пространства евклидова геометрия работает (сумма углов треугольника равна 180 и так далее). С другой точки зрения и другого масштаба все не так однозначно.
В завершение
Как показывает практика, законы, по которым существует мировая экономика (а таковые есть, только они не описаны), постоянно дают сбои. Система не равновесна, все глобальные прогнозы носят достаточно странный характер, потому как не сбываются. Очевидно, что многие процессы инертны, при этом взаимосвязи между множеством различных параметров, которые иногда и вовсе не сопоставляют, имеют место и являются более тонкими. Шахматные программы (и шахматные суперкомпьютеры) могут составить конкуренцию чемпионам только при условии наличия модуля расчета стратегической оценки ситуации на доске с учетом большого количества показателей. Но эти программы рассчитаны на победу, а не на удержание равновесия. Не так давно я задался весьма интересной задачей научно-практического толка, выраженной в создании шахматного интеллекта (алгоритма), который будет стремиться к уравновешиванию ситуации на доске, то есть постоянного сведения к ничьей независимо от уровня противника и разумности его ходов. А после, конечно, хочется связать это с равновесием по Джону Нэшу с учетом выявления стратегий. Говоря простыми словами, этот математик показал, что капиталистическая модель по Адаму Смиту, как бы это проще выразиться, сравнима с нашим вариантом 2+2=4, то есть работает, но в рамках определенного масштаба.
Думается, что и ученым со студентами в этом направлении также будет полезно подумать. При желании, конечно. Итак, на сегодня все.
Кристофер c.m.ihihoh@gmail.com
Билл Джой (Bill Joy)
Мировой финансовый кризис весьма интересен с математической точки зрения. Тут, конечно, явно напрашивается сравнение с психоисторией, предложенной в рамках фантастической трилогии с "Основаниями" Айзека Азимова, но и не только с ней. Играя в экономические стратегии (компьютерные игры), вы сталкиваетесь в большинстве случаев с тривиальнейшими экономическими моделями, которые построены по учебникам. Они являются частными случаями, но не более того. Причем с такими же моделями мы встречаемся и в жизни (если кто-то испугался сравнения с играми). Сегодня поговорим о том, что 2+2, кроме как в буквальном арифметическом смысле, не равно 4-м. Для этого немного попрограммируем, а те, кто не хотят, могут просто посмотреть на результаты, хотя предложенные примеры дадут волю фантазии экспериментаторам. После мы разовьем идею дальше.
Муар
В данном случае мы не будем говорить конкретно о технологии иллюзий, потому как результат оказывается очевидным и к разделу иллюзий как таковых его можно отнести с натяжкой.
Приведенный пример ваш покорный слуга решил показать на уровне Visual С#, причем с объяснением программирования, чтобы не столкнуться с такой же ситуацией, которая сложилась после публикации материала с дисками Бенхама, когда завалили тривиальными вопросами. Такой выбор языка сделан неспроста, поскольку он понятен большей части программистов, работающих на других схожих (С++, Java, Visual Basic и т.п.), является современным, перспективным и распространенным. Хотя нас пугают, что в Visual Studio 2010 он будет совмещен с Visual Basic (как говорят китайцы: "Чтоб ты жил в эпоху перемен"), C# очень удобен. На ActionScript также дадим небольшой идентичный листинг.
Задание — муар
Нам нужно создать и отобразить на форме два зеркальных и пересекающихся между собой массива отрезков. При этом в каждом из них эти самые отрезки не параллельны, а имеют небольшой и постоянный угол отклонения по отношению друг к другу.
Реализация
Итак, запускаем Visual C#, создаем новый проект Windows Application, назовем его Muar, нажимаем ОК, появляется чистая форма. В окне свойств этой формы мы меняем имя шапки на "Муар" (поле "Text"), устанавливаем размеры окна 500х500 (поле "Size"), вы можете предусмотреть свои варианты. Фоновым цветом окна формы (поле "Back Color") для лучшего восприятия устанавливаем белый. Все первоначальные настройки произведены, теперь в окне свойств переключаемся на события (Events, до этого мы были в закладке Properties), делаем двойной клик на строке Paint, в результате чего открывается окно с кодом для файла Form1.cs, и в появившейся нише записываем следующее:
private void Form1_Paint(object sender, PaintEventArgs e)
{
//малый и большой
//шаги, начальные
//координаты по Y
int h1 = 4, h2 = 6, y1 = 50, y2 =0;
//задаем цвет и
//толщину пера
Pen myPen = new Pen(Color.Black, 1);
//запускаем цикл на 79 итераций
for (; y1 < 371; y1 += h1)
{
y2 += h2;
//рисуем первые линии
e.Graphics.DrawLine(myPen, 20, y1, 480, y2);
//рисуем вторые линии
e.Graphics.DrawLine(myPen, 20, y2, 480, y1);
}
//Высвобождаем память,
//выделенную объекту myPen
myPen.Dispose();
}
Все! Программа готова. Build -> Build Solution (или Ctrl+Shift+B), Debug -> Start Without Debugging (или Ctrl+F5), появилось окно с пересекающимися прямыми линиями. Но данное пересечение дает интересный эффект — мы отчетливо видим сложный рисунок, который и называется муаром. Точно такой же эффект можно наблюдать при сложении складок тюлевых занавесок на окне.

Теперь рассмотрим пример более подробно, причем обратим внимание и на представленный рисунок с четырьмя изображениями. Итак, некая нелинейность у нас имеет место в силу того, что массив отрезков сужается с одной стороны. Сами линии мы рисуем, просто указывая координаты двух конечных точек, при этом в правой части они формируются с одним шагом, в левой — с другим. В принципе, муар уже появляется даже при прорисовке только первого массива отрезков (что показано на изображении 1) в силу того, что мы имеем компьютерный попиксельный вариант рисования без продуктивного сглаживания. То есть резкие изломы сами по себе уже формируют новые линии. В природе, как вы понимаете, такого не наблюдается.
При наложении друг на друга двух зеркальных массивов отрезков (что показано на изображении 2) мы отчетливо видим рисунок, появившийся в результате их взаимодействия. Он носит явно нелинейный характер. При этом, если мы захотим сделать вариант пересечения параллельных линий, то есть приравняв шаги формирования вершин с двух сторон, то получим результат в виде вертикальных полос (что показано на изображении 3) и при удалении точки просмотра — горизонтальных градиентов. А на изображении 4 вместо второго массива отрезков прямых линий мы вставили множество дуг, заменив внутри цикла соответствующую строку кода на:
e.Graphics.DrawArc(myPen, 20, y2, 450, 10, 180, -180);
Листинг я вам дал и для того, чтобы вы смогли начать экспериментировать. На самом деле можно добиться великолепных эффектов, и высшим пилотажем в этом деле является получение видимых изображений, текста, разноплановых узоров и так далее. Да и сам вариант нелинейного перетекания форм заслуживает восхищения математического и эстетического толка.
Поскольку отсутствие продуктивного сглаживания может многим не понравиться, к тому же данный программный код применим не для всех языков, позволим себе дать небольшой листинг такой же программы на флеше (ActionScript 2), который сейчас изучают школьники, и правильно делают. В этой среде немного другой способ рисования, причем один из самых эффективных методов сглаживания линий, который стоит на автомате. Итак, открываем Adobe Flash, выбираем создание проекта ActionScript 2.0, делаем активным окно Actions, при этом нажимаем указателем мыши на "кирпичике" первого кадра Layer 1. Когда будем вводить код, на этом "кирпичике" автоматически появится значок альфы.
Итак, что же мы вводим (даем без комментариев, и так все понятно):
this.createEmptyMovieClip("MUAR_mc",1);
i = 0;
h1 = 4;
h2 = 6;
y1 = 50;
y2 = 0;
with (MUAR_mc) {
lineStyle(1,0x000000,100);
while (i<80) {
y1 += h1;
y2 += h2;
moveTo(20,y1);
lineTo(480,y2);
moveTo(20,y2);
lineTo(480,y1);
i++;
}
}
Запускаем Debug, видим изображение.

Некоторые выводы
Почему в данном случае мы можем говорить, что 2+2 не равно 4-м?
Если мы берем какой-то частный случай и начинаем его рассматривать при уменьшенном масштабе, то очень редко можно догадаться, что он является фрагментом какой-то большей взаимосвязанной структуры.
Математики очень любят подобные эксперименты в силу того, что из двух простейших элементов возникает нечто сложное.
И действительно, в нашем примере мы сложили 79 линий плюс 79, но в результате при визуальном восприятии получили не 158, а гораздо больше. Так вот, если мы сильно уменьшим масштаб до того, чтобы видеть только, как две линии пересекаются с двумя, то будем думать, что общей их суммой является 4, то есть мы увидим просто 4 линии… При отдалении просмотра картина меняется. Отсюда можно сделать вывод, что обычная арифметика актуальна только для строго определенного масштаба.
Мало того, при сильном укрупнении масштаба вся картина превратится в совокупность кривых, а прямые отрезки, которых мы уже не сможем детализировать, становятся не видными. То есть, при близком просмотре результат один, при удаленном — абсолютно другой и неожиданный. Есть и еще одна тематическая параллель, для чего обратимся к интереснейшей истории.
Гаусс, Гаусс…
Бесспорно, Карл Фридрих Гаусс был великим математиком, но существовал один прецедент, за который некоторые ученые его недолюбливали, хотя и признавали заслуги. Речь идет о неевклидовой геометрии. Пятый постулат Евклида говорит, что параллельные линии никогда не пересекаются и как следствие сумма углов треугольника равна 180 градусов. Согласитесь, такой математике нас до сих пор учат в школе. Но вы можете нарисовать треугольник, например, на сфере, либо просто представить его на глобусе как два меридиана, пересекающие экватор, но при этом сходящиеся на полюсах. То есть, у экватора само пересечение идет под прямыми углами (т.е. 90 и 90, и мы уже получаем 180), но есть и еще один угол у полюса. Также есть и примеры с получением суммы углов меньшей, чем 180 градусов, то есть треугольник нужно поместить на поверхности с отрицательной кривизной (для наглядности представьте себе фрагмент песочных часов). Так вот, Гаусс это нашел, проработал, был способен решать задачи "в этой геометрии", но не захотел не только публиковать результаты своих исследований, но и просил своих друзей держать все в тайне. Карла Фридриха считали королем математики, и он в действительности мог уже тогда сделать революцию, но перестраховывался.
Однажды Гаусса попросили составить карту Ганноверского королевства. В принципе, это была задача абсолютно не его уровня, но многие думают, что математик взялся за это, поскольку собирался проверить свои догадки. Он соорудил особо точный прибор, измерения проводились с немецкой дотошностью, и (как опять же предполагают многие) Гаусс хотел проверить измерения углов больших пространственных треугольников и получить сумму не равную 180 градусам. Но… ему это не удалось. С одной стороны, Ганноверское королевство слишком мало в рамках неевклидовой геометрии применительно к земному шару, хотя интересно в данном случае то, что если бы у него была просто большая сфера и точные приборы, то, наверное, и карту не пришлось бы составлять. То есть не очень верится, что Гаусс бы до такого не додумался, а принялся измерять земной шар. С другой стороны, есть теоретические изыскания, а есть и практическая применимость. Измерив Ганноверское королевство, Гаусс убедился, что для практики все не имеет большого значения.
Чего боялся ученый? В некоторых его письмах друзьям были строки о том, что если он только заикнется об этой теме, его поднимут на смех. Но тут стоит напомнить о практическом смысле нововведений, который выглядел туманным.
В то же время, когда Гаусс "измерял" королевство, в 1826 г. в Казани Николай Лобачевский пытался прочитать на заседании университетского совета лекцию о "воображаемой геометрии" и был осмеян, даже до конца не дочитал. Но он публиковался, активно продвигая свою идею, несмотря на сопротивление. Причем Гаусс, увидев его труды в 1840 году в немецкой научной прессе, пришел в большое волнение, он поспособствовал принятию Лобачевского в члены-корреспонденты Геттингенской академии наук. Но… ничего не сделал, то есть не объявил неевклидову геометрию правильной, чего от него Лобачевский ждал. Гаусс даже начал изучать русский для того, чтобы прочитать все работы Николая Ивановича, но делал это скрытно, не перекинувшись с русским ученым даже одним словом.
Над тем смеялись, хотя одного сказанного во всеуслышание мнения Гаусса было бы достаточно для того, чтобы эту математику приняли. Не менее интересно ситуация развернулось с Яношем Бойаи — сыном друга Карла Фридриха. Тот написал свой труд о неевклидовой геометрии, когда ему еще не было 20-ти. Работу отослали Гауссу для рассмотрения. Ответ пришел через долгое время, в нем Гаусс сообщал, что сделал это открытие 30 лет назад и… все. Наверное, нужно пояснить некоторую специфику того времени. Гаусс был математиком номер один, он мог признать или не признать определенное направление, от его воли зависело практически все. Но он этого не сделал и в этот раз. Бойаи ждал признания хоть не себя, но хотя бы научной правды до самой смерти, в конце жизни он стал душевнобольным. Причем, что удивительно, до всего в плане неевклидовой геометрии додумался сам.
Но веселее всего обстояло дело с Бернхардом Риманом. Тот сначала защитил диссертацию в Геттингенском университете, причем восхитив тогда самого Гаусса. Потом стал искать работу, и для того чтобы получить одну из должностей, нужно было прочитать пробную лекцию. Ученый предложил три темы, а Гаусс, которому уже было 75 лет, выбрал себе на горе либо из спортивного интереса "основы геометрии".
Это было восхитительно. До сих пор Римана по праву считают одним из самых великих ученых, если не самым великим. А тогда, в отличие от того же Лобачевского и Боайи, которые отвергали пятый постулат, Бернхард Риман просто отверг всего Евклида, показав, что существует множество классов неевклидовых геометрий. Мало того, все держалось на его (Римана) собственных принципах, а многое было представлено без доказательств. Математики были в шоке, Гаусс молча вышел, от его друзей потом стало известно, что он пришел в "высочайшее изумление".
Итак, а теперь откроем "Советскую энциклопедию", ищем… Риман… Бернхард… Читаем: "Риманова геометрия… Изучает свойства многомерных пространств, в малых областях которых имеет место (с точностью до бесконечно малых второго порядка) евклидова геометрия (при этом все пространство может не быть евклидовым)". Конечно, ваш покорный слуга мог бы многое рассказать вам о Римане и без "Советской Энциклопедии", но тут и так все понятно. И странное дело, Лобачевский в своей теории все разложил по полочкам с доказательствами и так далее, но над ним смеялись и издевались (как показывают некоторые исторические заметки), Бойаи сошел от безысходности с ума, Гаусс боялся, что его, величайшего, вдруг поднимут на смех. А Риман злил всех и вся, доказательств минимум, реакция ученых не задевает, и если все ждали от Гаусса признания, то Бенхарда Римана оно вообще не сильно волновало.
А в общем и целом, если нас сейчас читают начинающие математики, то им следует присмотреться к Риману, потому как недоказанного и очень интересного у него осталось достаточно много.
А обычный читатель уже понял, к чему был этот рассказ, то есть, в рамках определенного масштаба и представленного определенным же образом пространства евклидова геометрия работает (сумма углов треугольника равна 180 и так далее). С другой точки зрения и другого масштаба все не так однозначно.
В завершение
Как показывает практика, законы, по которым существует мировая экономика (а таковые есть, только они не описаны), постоянно дают сбои. Система не равновесна, все глобальные прогнозы носят достаточно странный характер, потому как не сбываются. Очевидно, что многие процессы инертны, при этом взаимосвязи между множеством различных параметров, которые иногда и вовсе не сопоставляют, имеют место и являются более тонкими. Шахматные программы (и шахматные суперкомпьютеры) могут составить конкуренцию чемпионам только при условии наличия модуля расчета стратегической оценки ситуации на доске с учетом большого количества показателей. Но эти программы рассчитаны на победу, а не на удержание равновесия. Не так давно я задался весьма интересной задачей научно-практического толка, выраженной в создании шахматного интеллекта (алгоритма), который будет стремиться к уравновешиванию ситуации на доске, то есть постоянного сведения к ничьей независимо от уровня противника и разумности его ходов. А после, конечно, хочется связать это с равновесием по Джону Нэшу с учетом выявления стратегий. Говоря простыми словами, этот математик показал, что капиталистическая модель по Адаму Смиту, как бы это проще выразиться, сравнима с нашим вариантом 2+2=4, то есть работает, но в рамках определенного масштаба.
Думается, что и ученым со студентами в этом направлении также будет полезно подумать. При желании, конечно. Итак, на сегодня все.
Кристофер c.m.ihihoh@gmail.com
Компьютерная газета. Статья была опубликована в номере 14 за 2009 год в рубрике технологии


