Популярно об ИИ
Хотя задаваемые в рамках данных материалов вопросы предназначены для самостоятельного освоения и письма с ответами присылать было совсем не обязательно, все-таки нашлись люди, которые решили их написать. Самое удивительное, что некоторые ответы выглядели как отписки на тесты. Зачем высылать такое — для галочки? Здесь от вас такого не требуется. Впрочем, хоть и не нужно было ничего писать, я позволил себе провести некий небольшой статистический анализ. Особенно интересными были ответы на вопрос с переворотом теста Тьюринга, а именно — как машина может определить, что с ней общается человек. Большинство сошлось во мнении: из-за ошибок человека. Согласитесь, это выглядит странно, тем более что ИИ может ошибаться гораздо чаще, особенно если он неточно запрограммирован. Хотя у человека свои ошибки, у ИИ — свои…
В прошлом материале мы рассмотрели основные алгоритмы неинформированного поиска. Он используется во множестве сфер, например в тех же автономных роботах. С другой стороны, лучше, когда поиск является информированным. Например, из пункта А в пункт B гораздо удобнее добраться, имея сетку координат, а в рамках беспилотных машин это GPS. Все остальное зависит от самих алгоритмов, которые далеко не всегда работают без ошибок и являются оптимальными.
Сегодня мы перейдем к практике и решим несколько задач.
Миссионеры и каннибалы
На самом деле все, что излагалось ранее, является не таким простым, как может показаться. Вот, например, по описанию самая простейшая задача — а сколько трудностей она может вызвать! Она очень широко обсуждалась. Впервые была очень подробно проанализирована в 1968 году Амарелем, после чего была введена в проблематику ИИ представителями ныне узкоспециализированного направления Ньюэллом и Саймоном.
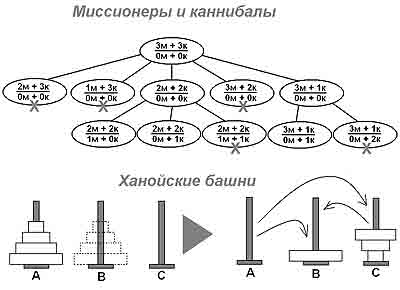
Задача звучит так. На одном берегу реки находятся три миссионера и три каннибала. Есть лодка, которая может вмещать одного или двух человек. Нужно перевезти всех на другой берег, при условии, что нигде не должна оставаться группа миссионеров меньшей численностью, чем каннибалов. Честно сказать, ваш покорный слуга не так давно узнал об этой задаче и решил ее без всяких деревьев поиска, просто до этого было решено очень много подобного. Но начинающие часто оказываются в тупике. Поэтому составляем дерево. В принципе, для того, чтобы показать сам ход решения, достаточно развернуть корневой узел на два уровня. На показанном рисунке вы видите схему. Начальное состояние описывается наличием 3 миссионеров и 3 каннибалов на одном берегу и отсутствием всех на втором (показано как 3м+3к/0м+0к). После этого мы должны посадить кого-то в лодку, причем ветви, которые предусматривают посадку только одного человека, мы в данном случае отметаем, потому как нужен человек, который должен привести лодку обратно.
Если мы посадим в лодку двух миссионеров, то нарушаем условия задачи, оставляя на берегу большее количество каннибалов. В результате остается только два варианта — отправить на другой берег либо одного миссионера и одного каннибала, либо двух каннибалов. В этом случае условие с оставляемым на берегу количеством соблюдено. Дальнейшее развитие идет по уже понятному направлению.
На втором уровне для упрощения представления мы исключили варианты, когда лодка приплывет к другому берегу и потом вернется обратно с тем же составом, который был отправлен. Хотя при составлении алгоритма это нужно обязательно учитывать.
Ханойские башни
 Предыдущий пример показал, как важно следить за порядком следования. Следующий пример — с "ханойскими башнями" — является классическим в области применения рекурсивных функций. Но об этом чуть позже, сначала опишем саму задачу.
Предыдущий пример показал, как важно следить за порядком следования. Следующий пример — с "ханойскими башнями" — является классическим в области применения рекурсивных функций. Но об этом чуть позже, сначала опишем саму задачу.
Имеется три стержня: A, B и C. На А нанизана сужающаяся кверху пирамида из дисков. Нужно переместить пирамиду в таком же виде на стержень B, при этом С можно использовать как вспомогательный.
Алгоритмически это решить достаточно просто, а именно: нужно создать функцию RingRemove, которая сначала сместит n-1 дисков со стержня А на С, потом поместит последний диск с А на В, а после переместит n-1 дисков с С на B.
С точки зрения программирования, чем больше дисков, тем более сложной является решение задачи, поэтому нужно использовать рекурсивные функции. Представим наше решение достаточно абстрактно:
void RingRemove (int n, char a, char b, char c)
{
if (n<=0) return;
RingRemove (n-1, a, c, b); // перемещаем n-1 дисков с А на С
… //здесь фрагмент кода, помещающий последний диск с A на B
RingRemove (n-1, с, b, a); // перемещаем n-1 дисков с C на B
}
Немного непонятно?
Несколько слов о рекурсивных функциях
В принципе, эту задачу можно решить и стандартными методами, но рекурсивные функции (функции, которые вызывают сами себя) в ряде случаев гораздо оптимальнее. Их можно назвать некоей уникальной "упаковкой" алгоритма, ведущей к значительной минимизации кода, это если не говорить об элегантности решения, которое очевидно. При этом есть правило, что любая задача, которая решается с помощью рекурсии, может быть решена и без нее, хотя уже сложилось так, что некоторые задачи не решаются без рекурсий вообще.
Классический пример — с вычислением факториала (произведение всех целых положительных чисел до данного значения). Известно, что если задано некое число n, то n! = 1*2*3*…*(n-2)*(n-1)*n. Конечно, реализовать алгоритм вычисления можно и с помощью цикла, но можно воспользоваться и рекурсией. Напишем код на С++:
int Fact(int n)
{
if (n==0) return 1; // факториал 0!=1
return n*Fact(n-1);
}
Рекурсивные функции реализуемы практически во всех языках программирования, даже в Бейсике, в качестве примера тот же код мы можем написать на ActionScript3 (Adobe Flash) как представителе языковой диаспоры ECMA-262:
function Fact(n:uint):int
{
if (n == 0) { return 1; }
else { return n*Fact(n-1); }
}
… а теперь объясним его. Следует ввести разделение между определением функции, которое может быть одно, и активацией функции — особого объекта данных, создаваемого при вызове функции на основании ее определения. Простыми словами — под активацией понимается выполняющаяся функция. Активаций может находиться в памяти сразу несколько, а очередь их выполнения называется стеком. В данном случае мы подразумеваем LIFO (последним пришел — первым ушел). То есть та активация, которая сформирована последней, будет выполняться первой.
На самом деле ничего непонятного, как кажется начинающим программистам, в этом нет. Ведь когда вы из одной функции вызываете другую, то первая ждет выполнения второй. На этом же принципе и основана рекурсия, ведь различий в том, вызывается ли сторонняя функция либо функция вызывает саму себя, нет.
Теперь смотрим, как будет согласно нашему коду вычисляться факториал 3. 3 не равно 0, поэтому идет вычисление n*Fact(n-1), при этом осуществляется вызов Fact() с параметром n=2, таким образом, создается второй объект активации, который располагается в стеке первым. После дальнейших итераций появляются новые объекты активации с параметрами n=1 и n=0. При этом понятно, что 1*Fact(0) имеет конечное значение, данный объект активации выполняется первым и выгружается. После этого идет разрушение следующих активаций, и ответом на 3! будет 6.
Факториалы, вычисление степеней и так далее очень часто отображены в литературе в качестве классических примеров рекурсии, хотя на самом деле они не являются оптимальными, потому как проще использовать циклы (это раз), к тому же во многих языках и в реальных условиях цепь рекурсивных объектов активации не может быть бесконечной (это два). Например, раньше в том же ActionScript размер стека был ограничен 256 элементами, то есть факториал 400 вы там не сможете вычислить с помощью рекурсии.
На самом деле по рекурсивным алгоритмам выпускаются целые книги и справочные материалы, которые достаточно редки в силу узкой специализации, но очень полезны в применении. Например, в вариантах создания сложных моделей поиска решений и так далее. Для лучшего понимания вопроса рекомендуется самостоятельно попробовать заменить функции, предусматривающие циклические вычисления на рекурсивный метод.
Задача с восемью ферзями
Идея проста: нужно расположить на шахматной доске 8х8 восемь ферзей таким образом, чтобы ни один из них не оказался под атакой другого. Не будем долго рассуждать о теоретических основах данной задачи, ведь это — классический пример практически во всех книгах по ИИ, а посмотрим, как ее решение можно реализовать на практике.
Итак, ферзь — это дальнобойная фигура, атакующая по вертикали, горизонтали и диагонали. Наш поиск будет включать один важный элемент — анализ предыдущих состояний.
То есть X и Y являются координатами клеток. Соответственно, ставя нового ферзя, нужно учитывать, что X или Y выбранной клетки не совпадает с уже имеющимися, на которых стоят ферзи. Что касается диагоналей, то несложно догадаться, что для нисходящей "\" величина X+Y будет являться одинаковой, а для восходящей "/" одинаковой будет X-Y.
Таким образом мы формируем четыре условия, которых на самом деле получится три, потому как X или Y мы можем взять за шаг поиска. А сам алгоритм лучше всего реализуется с помощью рекурсивной функции.
Задача Эйлера
Эту задачу любят решать школьники — нужно обойти конем шахматную доску таким образом, чтобы в каждой клетке фигура побывала только один раз. Тонкости решения программным образом состоят в том, что ход коня не так прямолинеен, как ферзя. То есть нужно прописывать правила. После чего применяется рекурсия на глубину 64 (по количеству клеток).
Промежуточное завершение
Вообще, хорошо написанным емким алгоритмом, элегантным решением можно любоваться как произведением искусства. Известная фраза о том, что не всегда хорошее планирование заменит хорошую импровизацию, созвучна понятию "ручной доводки", о которой так часто пишут многочисленные авторы проектов. Но ту же задачу Эйлера, как и с ферзями, можно начать решать таким громоздким способом, что любая импровизация и "ручная доводка" в дальнейшем процессе не помогут. Основной проблемой ИИ как научной дисциплины является поиск оптимальной методологии для решения сложных задач, для чего исследуется множество смежных дисциплин и собираются "сливки".
Кристофер christopher@tut.by
В прошлом материале мы рассмотрели основные алгоритмы неинформированного поиска. Он используется во множестве сфер, например в тех же автономных роботах. С другой стороны, лучше, когда поиск является информированным. Например, из пункта А в пункт B гораздо удобнее добраться, имея сетку координат, а в рамках беспилотных машин это GPS. Все остальное зависит от самих алгоритмов, которые далеко не всегда работают без ошибок и являются оптимальными.
Сегодня мы перейдем к практике и решим несколько задач.
Миссионеры и каннибалы
На самом деле все, что излагалось ранее, является не таким простым, как может показаться. Вот, например, по описанию самая простейшая задача — а сколько трудностей она может вызвать! Она очень широко обсуждалась. Впервые была очень подробно проанализирована в 1968 году Амарелем, после чего была введена в проблематику ИИ представителями ныне узкоспециализированного направления Ньюэллом и Саймоном.
Задача звучит так. На одном берегу реки находятся три миссионера и три каннибала. Есть лодка, которая может вмещать одного или двух человек. Нужно перевезти всех на другой берег, при условии, что нигде не должна оставаться группа миссионеров меньшей численностью, чем каннибалов. Честно сказать, ваш покорный слуга не так давно узнал об этой задаче и решил ее без всяких деревьев поиска, просто до этого было решено очень много подобного. Но начинающие часто оказываются в тупике. Поэтому составляем дерево. В принципе, для того, чтобы показать сам ход решения, достаточно развернуть корневой узел на два уровня. На показанном рисунке вы видите схему. Начальное состояние описывается наличием 3 миссионеров и 3 каннибалов на одном берегу и отсутствием всех на втором (показано как 3м+3к/0м+0к). После этого мы должны посадить кого-то в лодку, причем ветви, которые предусматривают посадку только одного человека, мы в данном случае отметаем, потому как нужен человек, который должен привести лодку обратно.
Если мы посадим в лодку двух миссионеров, то нарушаем условия задачи, оставляя на берегу большее количество каннибалов. В результате остается только два варианта — отправить на другой берег либо одного миссионера и одного каннибала, либо двух каннибалов. В этом случае условие с оставляемым на берегу количеством соблюдено. Дальнейшее развитие идет по уже понятному направлению.
На втором уровне для упрощения представления мы исключили варианты, когда лодка приплывет к другому берегу и потом вернется обратно с тем же составом, который был отправлен. Хотя при составлении алгоритма это нужно обязательно учитывать.
Ханойские башни

Имеется три стержня: A, B и C. На А нанизана сужающаяся кверху пирамида из дисков. Нужно переместить пирамиду в таком же виде на стержень B, при этом С можно использовать как вспомогательный.
Алгоритмически это решить достаточно просто, а именно: нужно создать функцию RingRemove, которая сначала сместит n-1 дисков со стержня А на С, потом поместит последний диск с А на В, а после переместит n-1 дисков с С на B.
С точки зрения программирования, чем больше дисков, тем более сложной является решение задачи, поэтому нужно использовать рекурсивные функции. Представим наше решение достаточно абстрактно:
void RingRemove (int n, char a, char b, char c)
{
if (n<=0) return;
RingRemove (n-1, a, c, b); // перемещаем n-1 дисков с А на С
… //здесь фрагмент кода, помещающий последний диск с A на B
RingRemove (n-1, с, b, a); // перемещаем n-1 дисков с C на B
}
Немного непонятно?
Несколько слов о рекурсивных функциях
В принципе, эту задачу можно решить и стандартными методами, но рекурсивные функции (функции, которые вызывают сами себя) в ряде случаев гораздо оптимальнее. Их можно назвать некоей уникальной "упаковкой" алгоритма, ведущей к значительной минимизации кода, это если не говорить об элегантности решения, которое очевидно. При этом есть правило, что любая задача, которая решается с помощью рекурсии, может быть решена и без нее, хотя уже сложилось так, что некоторые задачи не решаются без рекурсий вообще.
Классический пример — с вычислением факториала (произведение всех целых положительных чисел до данного значения). Известно, что если задано некое число n, то n! = 1*2*3*…*(n-2)*(n-1)*n. Конечно, реализовать алгоритм вычисления можно и с помощью цикла, но можно воспользоваться и рекурсией. Напишем код на С++:
int Fact(int n)
{
if (n==0) return 1; // факториал 0!=1
return n*Fact(n-1);
}
Рекурсивные функции реализуемы практически во всех языках программирования, даже в Бейсике, в качестве примера тот же код мы можем написать на ActionScript3 (Adobe Flash) как представителе языковой диаспоры ECMA-262:
function Fact(n:uint):int
{
if (n == 0) { return 1; }
else { return n*Fact(n-1); }
}
… а теперь объясним его. Следует ввести разделение между определением функции, которое может быть одно, и активацией функции — особого объекта данных, создаваемого при вызове функции на основании ее определения. Простыми словами — под активацией понимается выполняющаяся функция. Активаций может находиться в памяти сразу несколько, а очередь их выполнения называется стеком. В данном случае мы подразумеваем LIFO (последним пришел — первым ушел). То есть та активация, которая сформирована последней, будет выполняться первой.
На самом деле ничего непонятного, как кажется начинающим программистам, в этом нет. Ведь когда вы из одной функции вызываете другую, то первая ждет выполнения второй. На этом же принципе и основана рекурсия, ведь различий в том, вызывается ли сторонняя функция либо функция вызывает саму себя, нет.
Теперь смотрим, как будет согласно нашему коду вычисляться факториал 3. 3 не равно 0, поэтому идет вычисление n*Fact(n-1), при этом осуществляется вызов Fact() с параметром n=2, таким образом, создается второй объект активации, который располагается в стеке первым. После дальнейших итераций появляются новые объекты активации с параметрами n=1 и n=0. При этом понятно, что 1*Fact(0) имеет конечное значение, данный объект активации выполняется первым и выгружается. После этого идет разрушение следующих активаций, и ответом на 3! будет 6.
Факториалы, вычисление степеней и так далее очень часто отображены в литературе в качестве классических примеров рекурсии, хотя на самом деле они не являются оптимальными, потому как проще использовать циклы (это раз), к тому же во многих языках и в реальных условиях цепь рекурсивных объектов активации не может быть бесконечной (это два). Например, раньше в том же ActionScript размер стека был ограничен 256 элементами, то есть факториал 400 вы там не сможете вычислить с помощью рекурсии.
На самом деле по рекурсивным алгоритмам выпускаются целые книги и справочные материалы, которые достаточно редки в силу узкой специализации, но очень полезны в применении. Например, в вариантах создания сложных моделей поиска решений и так далее. Для лучшего понимания вопроса рекомендуется самостоятельно попробовать заменить функции, предусматривающие циклические вычисления на рекурсивный метод.
Задача с восемью ферзями
Идея проста: нужно расположить на шахматной доске 8х8 восемь ферзей таким образом, чтобы ни один из них не оказался под атакой другого. Не будем долго рассуждать о теоретических основах данной задачи, ведь это — классический пример практически во всех книгах по ИИ, а посмотрим, как ее решение можно реализовать на практике.
Итак, ферзь — это дальнобойная фигура, атакующая по вертикали, горизонтали и диагонали. Наш поиск будет включать один важный элемент — анализ предыдущих состояний.
То есть X и Y являются координатами клеток. Соответственно, ставя нового ферзя, нужно учитывать, что X или Y выбранной клетки не совпадает с уже имеющимися, на которых стоят ферзи. Что касается диагоналей, то несложно догадаться, что для нисходящей "\" величина X+Y будет являться одинаковой, а для восходящей "/" одинаковой будет X-Y.
Таким образом мы формируем четыре условия, которых на самом деле получится три, потому как X или Y мы можем взять за шаг поиска. А сам алгоритм лучше всего реализуется с помощью рекурсивной функции.
Задача Эйлера
Эту задачу любят решать школьники — нужно обойти конем шахматную доску таким образом, чтобы в каждой клетке фигура побывала только один раз. Тонкости решения программным образом состоят в том, что ход коня не так прямолинеен, как ферзя. То есть нужно прописывать правила. После чего применяется рекурсия на глубину 64 (по количеству клеток).
Промежуточное завершение
Вообще, хорошо написанным емким алгоритмом, элегантным решением можно любоваться как произведением искусства. Известная фраза о том, что не всегда хорошее планирование заменит хорошую импровизацию, созвучна понятию "ручной доводки", о которой так часто пишут многочисленные авторы проектов. Но ту же задачу Эйлера, как и с ферзями, можно начать решать таким громоздким способом, что любая импровизация и "ручная доводка" в дальнейшем процессе не помогут. Основной проблемой ИИ как научной дисциплины является поиск оптимальной методологии для решения сложных задач, для чего исследуется множество смежных дисциплин и собираются "сливки".
Кристофер christopher@tut.by
Компьютерная газета. Статья была опубликована в номере 25 за 2008 год в рубрике технологии


