Популярно об ИИ
Алгоритмы, не запоминающие результаты своих действий, могут войти в состояние бесконечного цикла…
Практически все и всегда нужно оптимизировать. Даже код, который вы взяли из книги или методы, которые изложены там как основополагающие. С точки зрения поиска решений, который мы сегодня будем подробно обсуждать, оптимизации нужно подвергать не только алгоритмическую модель, но и саму задачу, представление входящих данных. Держа в руках карту и выбирая маршрут, человек практически автоматически отметает неперспективные ветви. Но тому же компьютеру это нужно объяснять… и даже более того.
Казалось бы, что может быть проще нахождения оптимального маршрута? С подобными алгоритмами поиска вы часто сталкиваетесь в различных видах ПО. Но на самом деле не все так тривиально.
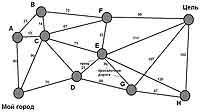Итак, на первом рисунке отображена некая карта, отправным населенным пунктом является "Мой город", местом прибытия — "Цель", а промежуточные обозначены латинскими буквами A-H. Расстояния в километрах показаны цифрами. Теперь имеет смысл составить дерево поиска, где "Мой город" будет выступать в качестве начального состояния и поискового узла. Начинаем все разворачивать и говорим озадаченно: "Упс-с!".
На данный момент следует ввести разграничение между понятиями "узел" и "состояние". Под узлами нужно понимать некие вещественные части структуры данных для того же дерева поиска, в то время как состояния описывают конфигурацию мира. Чтобы было проще понять, давайте возьмем для примера узел А, при этом есть состояние "въезд в А", которое может быть достигнуто по различным маршрутам, то есть поисковым ветвям. И, например, каждый узел, кроме корневого, в рамках выстраиваемых ветвей имеет свой родительский, в то время как состояния не располагают ничем подобным. На нашей карте мы имеем 10 состояний ("въезд" в 10 населенных пунктов), но вариантов путей, которые к ним приводят, существует бесконечное множество. Почему их так много "в машинном понимании", вы поймете чуть позже. Сама же карта является ничем иным как пространством состояний, или, проще говоря, графом. Для тех, кто незнаком с этим понятием, отметим, что граф — это графическое/геометрическое представление математической модели в виде вершин и соединяющих их связующих ребер. Как он выглядит, вы можете увидеть на примере нашей карты: населенные пункты — вершины, дороги — ребра.
Итак, мы имеем начальное состояние "Мой город", после чего в дереве поиска производим его развертывание до следующего множества состояний, а именно — въезда в А, С и D. После этого мы предусмотрим вариант полного перебора и начнем строить ветви дальше. Например, из узла А вы можете вернуться в "Мой город", а также направиться в B и С. Порядок, в котором мы начинаем развертывать ветви состояний, именуется стратегией поиска. Стоит отметить также применяемую терминологию. При развертывании узла "Мой город" оный является родительским по отношению к A, C, D, а они, в свою очередь, дочерние по отношению к нему (преемники), при этом A и C являются сестринскими к D и так далее. Листовым узлом называется тот, у которого нет преемников.
Среди стратегий поиска в рамках представления Tree-Search (поиск по дереву) можно выделить семь ключевых:
. В ширину. Полный перебор всех ветвей с движением от уровня к уровню. То есть сначала рассматриваются все узлы на одном уровне, после чего осуществляется переход к следующему. Последовательная очередь перебора формируется как FIFO (First-In-First-Out, "первый пришел — первым и ушел").
. По стоимости. В данном случае мы лишь косвенно подразумеваем нашу задачу, где мерилом стоимости является расстояние в километрах. То есть ее можно решить и таким методом, вычислив стоимость пути для каждой ветви дерева, начав с путей, предусматривающих минимальную стоимость, а почему это не так хорошо подходит, вы поймете чуть позже.
. В глубину. Если в варианте "в ширину" мы предусматривали поэтапное движение от уровня к уровню с перебором всех узлов, на них содержащихся, то в данном случае само движение идет по вертикали, то есть по ветвям. Каждая из них развертывается до самого глубокого уровня, на котором узлы уже не имеют преемников, после чего берется следующая ветвь, начиная с того узла, в котором есть неисследованные преемники. Вычисления идут поэтапно от узла к узлу по ветви, а последовательная очередь формируется как LIFO (Last-In-First-Out, "последний пришел — первым ушел", — об этом мы подробно поговорим в следующем материале). Как альтернативу данному варианту поиска в большинстве случаев применяют алгоритмы с рекурсивной функцией. При расчетах хранится только одно значение текущего узла, а все предыдущие по ветви, которые к нему привели, удаляются из памяти. То есть для тех, кто не знает о рекурсии, отметим, что в данном случае используется функция, которая сама себя вызывает каждый раз при переходе к дочернему узлу по ветви. Результатом ее действия является получение информации о листовом узле. Данные вычисления являются одними из самых оптимальных в плане затрат аппаратных мощностей и очень часто используются в программировании. . Поиск на определенную глубину. Об этом поговорим чуть позже на конкретном примере.
. Поиск в глубину с итеративным углублением. По существу, вычисления идут в глубину до определенного уровня, но если цель не достигнута, глубина увеличивается. В нашем случае этот метод не очень подходит, поскольку не дает самый оптимальный маршрут, причем очень многое зависит от очереди вычислений и некоторых других факторов.
. Двунаправленный поиск. Сам поиск идет одновременно с двух сторон — от начального состояния и от цели. Решение возникает, если ветви встречаются.
Последний вариант достаточно выгоден в силу того, что нужно использовать меньшее количество развернутых ветвей. Ведь с увеличением глубины их количество может расти с экспоненциальным увеличением для простейших бинарных деревьев, а для нашего примера еще круче, — а это затраты на вычисления. В рамках поиска по деревьям существует такой параметр, как коэффициент ветвления, который напрямую связан со сложностью и количеством производимых операций. Так вот в двунаправленном методе поиска мы получаем оптимальный вариант, когда ветвление не достигает критического уровня.
Выбор алгоритма и его улучшение
Что же нам может дать развертывание узлов и составление ветвей дерева в качестве руководства для дальнейших действий? Главным образом наглядность. Мы можем наблюдать, как решение задачи "видит" компьютер.
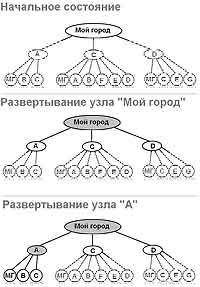Для нас естественно, а для него нет, что варианты "Мой город" ( A ( "Мой город" ( A ( "Мой город" являются самыми критическими, поскольку вычисление таких маршрутов будет производиться бесконечно. Конечно, многие могут предположить, что как минимум можно поставить программное "табу" на обращение к родительскому узлу, но это не так удобно. Ведь есть и более сложные варианты, когда ветвь поиска, пройдя через множество узлов, замкнется в кольцо на том же "Моем городе", обходя родительские узлы, например, "Мой город" ( D ( E ( F ( B ( A ( "Мой город". Такие вычисления также могут привести к бесконечности.
Что можно сделать в данной ситуации? Если использовать в качестве основы дерево поиска, в котором, как мы уже догадались, есть бесконечные ветви, то обратим свое внимание на карту. Несложно посчитать, что максимумом для достижения любого из городов является прохождение через восемь промежуточных узлов, то есть девять этапов. Эта величина называется диаметром пространства состояний. Таким образом, можно и не ставить никаких программных "табу" и не вносить какие-либо исключения, а просто предусмотреть поиск на глубину 9. То есть даже если есть циклические ветви, они не уйдут в бесконечность из-за введенного ограничения. Как успешные будут учитываться только те ветви, которые дают искомый результат — достижение цели. В качестве их оценки мы будем считать стоимость пути, в данном случае выраженную в километрах.
Но при этом есть и такое понятие, или, вернее, параметр, как стоимость поиска. Он показывает затрачиваемые на вычисления ресурсы (выделяемую память) и время самого поиска, которое высчитывается по количеству производимых операций (количеству развертываемых узлов). Поэтому, чтобы уменьшить данную стоимость, ограничения по обращению к родительским узлам, исключения циклично замкнутых ветвей вводить нужно. Как это сделать оптимальным образом? На самом деле метод, представленный как дерево поиска Tree-Search, не всегда является до конца оптимальным. Как вы могли заметить, мы многое упростили в расчетах, просто взглянув на карту, по существу являющуюся графом. И попробуем определить вариант Graph-Search. Сначала договоримся, что мы формируем два списка: закрытый и открытый, а сама функция запоминает значения состояний, которые уже были найдены. В первый список мы вносим узлы, которые уже развернуты, во второй — которые нет. Таким образом, развернув корневой узел до A, С и D, мы вносим его в закрытый список. В свою очередь, развернув их, мы также добавляем данные три узла в закрытый список. Если определенная ветвь поиска приходит к любому узлу из данного списка, она может быть отметена.
Но… у нас задача несколько сложнее, поэтому при достижении такого узла "окольными путями" мы должны сравнивать стоимость достижения соответствующего состояния, выраженную в расстояниях пути. То есть перед тем как отмести данную ветку, нам нужно сделать сравнение стоимости. Если найденный новый путь является более коротким и его стоимость меньше той, что имелась раньше, то значение заменяется и отметается предыдущая ветвь поиска. Для примера, на карте вы можете рассмотреть узел B, который является одновременно дочерним для узлов из множества ветвей дерева поиска. Соответственно, значение его стоимости при каждом расчете нужно сравнивать с уже имеющимся.
Таким образом, искомого результата в нашем примере мы можем достичь сразу несколькими алгоритмическими моделями:
. поиск в глубину с помощью рекурсии до 9 уровня*;
. поиск в глубину с помощью рекурсии до 9 уровня с оптимизацией, исключающей расчеты цикличных ветвей. В более сложных задачах такая оптимизация может уменьшить количество расчетов по экспоненциальному закону, то есть значительно;
. поиск в ширину до 9 уровня*;
. поиск в ширину по стоимости с оптимизацией, исключающей расчеты цикличных ветвей. То есть, нужно выделить только перспективные ветви; . Graph-Search, то есть Tree-Search с закрытым и открытым списками.
* — обратите внимание, что, взяв в учет глубину 9, мы предусмотрели вариант перебора всех возможных решений, но… посмотрев на карту, вы можете без труда увидеть, что нужное нам находится уже на третьем уровне.
В данном случае мы рассмотрели варианты неинформированного поиска, при котором результат ищется в рамках данных, которые представлены в описании задачи, и предметная область не расматривается. По существу, можно получить конкретный ответ о том, достигнута цель или нет, но при этом не используются методы выявления наибольшей вероятности нахождения оптимального решения, выбора нужной ветки и так далее.
Чтобы легче было понять сказанное, рассмотрим следующий пример.
А*-поиск
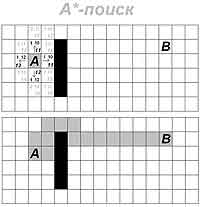Данный алгоритм относится к информированному (эвристическому) поиску и активно используется во многих сферах, например, в тех же играх, когда персонажу нужно достичь цели на карте по наиболее короткому пути с учетом огибания препятствий.
Нужно отметить, что сам алгоритм весьма прост как в объяснении, так и в реализации, хотя стоит отметить несколько его разновидностей, которые применимы или нет в зависимости от сложности и специфики поставленной задачи.
Мы же сейчас рассмотрим самый простейший пример на небольшой игровой карте. Допустим, наш персонаж должен добраться с клетки А на клетку B по кратчайшему пути, обогнув небольшое препятствие, причем упростим задачу до того, что он может двигаться только по вертикали и горизонтали. Каждая из клеток в данном случае и будет являться узлом. Для начала отправную клетку (корневой узел) заносим в закрытый список, при этом видим, что герой может идти только по четырем направлениям.
Как мы будем их оценивать и что брать за стоимость? В данном случае вполне достаточно вычислять ее из двух величин:
. расстояние исследуемой клетки от начальной позиции. Высчитывается как сумма клеток по горизонтали и вертикали между отправным пунктом и конкретным узлом;
. расстояние от исследуемой клетки до цели. Высчитывается как сумма клеток по горизонтали и вертикали между конкретным узлом и целью. А суммарная стоимость будет являться суммой этих двух величин. И чем она меньше, тем оптимальнее сам ход (эта сумма показана курсивом). И так вычисляется один узел за другим, с внесением наиболее оптимальных (с наименьшей стоимостью) клеток в закрытый список, пока в открытом списке не появится клетка цели. После этого формируется маршрут.
Как вы могли заметить, на предложенном рисунке две клетки, расположенные возле А, имеют одинаковую стоимость, что может подразумевать некоторые проблемы. На самом деле от них можно избавиться различными путями, например, взять в учет только ту клетку, которая идет первой по открытому списку, либо предусмотреть случайный режим, хотя в реальной практике все несколько и сложнее, и проще одновременно, потому как стоимость каждой клетки может складываться из множества дополнительных составляющих.
***
Возвращаясь к примеру с картой населенных пунктов, можно отметить, что она очень быстро решаема в рамках применения алгоритма A*-поиска, если разместить саму карту на сетке координат. То есть, вычислив суммарную стоимость узлов относительно расстояния от начального пункта следования и от цели, вы без труда получите результат "Мой город" ( D ( E ( "Цель", который и будет являться правильным решением. Причем сам алгоритм будет работать даже в случае, когда, например, между пунктами E и "Цель" отсутствует дорога. Тогда будет успешно рассчитан другой маршрут, и он будет наиболее коротким. Проблемы могут возникнуть в случаях, когда дороги не являются ровными, и, например, расстояние DE будет большим, чем DG. В данном случае сетка координат с населенными пунктами не поможет, и нужно предусматривать более сложные варианты, например с разбиением на большее количество узлов.
Абстрагирование
На самом деле одним из ключевых моментов при постановке задачи поиска является отделение зерен от плевел, другими словами, абстрагирование. То есть выдача только необходимых и оптимальных данных при описании задания.
Допустим, в населенном пункте B находится красивый замок, и путешественник хочет его обязательно посетить. Таким образом, нужно составить другой оптимальный маршрут и при стоимости узлов для поиска учитывать данный момент. Также на карте вы можете найти два места — "грязь" и "проселочная дорога", которые при определенных обстоятельствах нужно учитывать в стоимости. Но если человеку все равно, увидит он этот замок или нет, то такая информация будет абсолютно ненужной, как, например, для составления маршрута все равно, какой будет вид из окна, если это не входит в требуемые условия задачи. И особенно важно это при постановке задач для неинформированного поиска.
Кристофер christopher@tut.by
Практически все и всегда нужно оптимизировать. Даже код, который вы взяли из книги или методы, которые изложены там как основополагающие. С точки зрения поиска решений, который мы сегодня будем подробно обсуждать, оптимизации нужно подвергать не только алгоритмическую модель, но и саму задачу, представление входящих данных. Держа в руках карту и выбирая маршрут, человек практически автоматически отметает неперспективные ветви. Но тому же компьютеру это нужно объяснять… и даже более того.
Казалось бы, что может быть проще нахождения оптимального маршрута? С подобными алгоритмами поиска вы часто сталкиваетесь в различных видах ПО. Но на самом деле не все так тривиально.
На данный момент следует ввести разграничение между понятиями "узел" и "состояние". Под узлами нужно понимать некие вещественные части структуры данных для того же дерева поиска, в то время как состояния описывают конфигурацию мира. Чтобы было проще понять, давайте возьмем для примера узел А, при этом есть состояние "въезд в А", которое может быть достигнуто по различным маршрутам, то есть поисковым ветвям. И, например, каждый узел, кроме корневого, в рамках выстраиваемых ветвей имеет свой родительский, в то время как состояния не располагают ничем подобным. На нашей карте мы имеем 10 состояний ("въезд" в 10 населенных пунктов), но вариантов путей, которые к ним приводят, существует бесконечное множество. Почему их так много "в машинном понимании", вы поймете чуть позже. Сама же карта является ничем иным как пространством состояний, или, проще говоря, графом. Для тех, кто незнаком с этим понятием, отметим, что граф — это графическое/геометрическое представление математической модели в виде вершин и соединяющих их связующих ребер. Как он выглядит, вы можете увидеть на примере нашей карты: населенные пункты — вершины, дороги — ребра.
Итак, мы имеем начальное состояние "Мой город", после чего в дереве поиска производим его развертывание до следующего множества состояний, а именно — въезда в А, С и D. После этого мы предусмотрим вариант полного перебора и начнем строить ветви дальше. Например, из узла А вы можете вернуться в "Мой город", а также направиться в B и С. Порядок, в котором мы начинаем развертывать ветви состояний, именуется стратегией поиска. Стоит отметить также применяемую терминологию. При развертывании узла "Мой город" оный является родительским по отношению к A, C, D, а они, в свою очередь, дочерние по отношению к нему (преемники), при этом A и C являются сестринскими к D и так далее. Листовым узлом называется тот, у которого нет преемников.
Среди стратегий поиска в рамках представления Tree-Search (поиск по дереву) можно выделить семь ключевых:
. В ширину. Полный перебор всех ветвей с движением от уровня к уровню. То есть сначала рассматриваются все узлы на одном уровне, после чего осуществляется переход к следующему. Последовательная очередь перебора формируется как FIFO (First-In-First-Out, "первый пришел — первым и ушел").
. По стоимости. В данном случае мы лишь косвенно подразумеваем нашу задачу, где мерилом стоимости является расстояние в километрах. То есть ее можно решить и таким методом, вычислив стоимость пути для каждой ветви дерева, начав с путей, предусматривающих минимальную стоимость, а почему это не так хорошо подходит, вы поймете чуть позже.
. В глубину. Если в варианте "в ширину" мы предусматривали поэтапное движение от уровня к уровню с перебором всех узлов, на них содержащихся, то в данном случае само движение идет по вертикали, то есть по ветвям. Каждая из них развертывается до самого глубокого уровня, на котором узлы уже не имеют преемников, после чего берется следующая ветвь, начиная с того узла, в котором есть неисследованные преемники. Вычисления идут поэтапно от узла к узлу по ветви, а последовательная очередь формируется как LIFO (Last-In-First-Out, "последний пришел — первым ушел", — об этом мы подробно поговорим в следующем материале). Как альтернативу данному варианту поиска в большинстве случаев применяют алгоритмы с рекурсивной функцией. При расчетах хранится только одно значение текущего узла, а все предыдущие по ветви, которые к нему привели, удаляются из памяти. То есть для тех, кто не знает о рекурсии, отметим, что в данном случае используется функция, которая сама себя вызывает каждый раз при переходе к дочернему узлу по ветви. Результатом ее действия является получение информации о листовом узле. Данные вычисления являются одними из самых оптимальных в плане затрат аппаратных мощностей и очень часто используются в программировании. . Поиск на определенную глубину. Об этом поговорим чуть позже на конкретном примере.
. Поиск в глубину с итеративным углублением. По существу, вычисления идут в глубину до определенного уровня, но если цель не достигнута, глубина увеличивается. В нашем случае этот метод не очень подходит, поскольку не дает самый оптимальный маршрут, причем очень многое зависит от очереди вычислений и некоторых других факторов.
. Двунаправленный поиск. Сам поиск идет одновременно с двух сторон — от начального состояния и от цели. Решение возникает, если ветви встречаются.
Последний вариант достаточно выгоден в силу того, что нужно использовать меньшее количество развернутых ветвей. Ведь с увеличением глубины их количество может расти с экспоненциальным увеличением для простейших бинарных деревьев, а для нашего примера еще круче, — а это затраты на вычисления. В рамках поиска по деревьям существует такой параметр, как коэффициент ветвления, который напрямую связан со сложностью и количеством производимых операций. Так вот в двунаправленном методе поиска мы получаем оптимальный вариант, когда ветвление не достигает критического уровня.
Выбор алгоритма и его улучшение
Что же нам может дать развертывание узлов и составление ветвей дерева в качестве руководства для дальнейших действий? Главным образом наглядность. Мы можем наблюдать, как решение задачи "видит" компьютер.
Что можно сделать в данной ситуации? Если использовать в качестве основы дерево поиска, в котором, как мы уже догадались, есть бесконечные ветви, то обратим свое внимание на карту. Несложно посчитать, что максимумом для достижения любого из городов является прохождение через восемь промежуточных узлов, то есть девять этапов. Эта величина называется диаметром пространства состояний. Таким образом, можно и не ставить никаких программных "табу" и не вносить какие-либо исключения, а просто предусмотреть поиск на глубину 9. То есть даже если есть циклические ветви, они не уйдут в бесконечность из-за введенного ограничения. Как успешные будут учитываться только те ветви, которые дают искомый результат — достижение цели. В качестве их оценки мы будем считать стоимость пути, в данном случае выраженную в километрах.
Но при этом есть и такое понятие, или, вернее, параметр, как стоимость поиска. Он показывает затрачиваемые на вычисления ресурсы (выделяемую память) и время самого поиска, которое высчитывается по количеству производимых операций (количеству развертываемых узлов). Поэтому, чтобы уменьшить данную стоимость, ограничения по обращению к родительским узлам, исключения циклично замкнутых ветвей вводить нужно. Как это сделать оптимальным образом? На самом деле метод, представленный как дерево поиска Tree-Search, не всегда является до конца оптимальным. Как вы могли заметить, мы многое упростили в расчетах, просто взглянув на карту, по существу являющуюся графом. И попробуем определить вариант Graph-Search. Сначала договоримся, что мы формируем два списка: закрытый и открытый, а сама функция запоминает значения состояний, которые уже были найдены. В первый список мы вносим узлы, которые уже развернуты, во второй — которые нет. Таким образом, развернув корневой узел до A, С и D, мы вносим его в закрытый список. В свою очередь, развернув их, мы также добавляем данные три узла в закрытый список. Если определенная ветвь поиска приходит к любому узлу из данного списка, она может быть отметена.
Но… у нас задача несколько сложнее, поэтому при достижении такого узла "окольными путями" мы должны сравнивать стоимость достижения соответствующего состояния, выраженную в расстояниях пути. То есть перед тем как отмести данную ветку, нам нужно сделать сравнение стоимости. Если найденный новый путь является более коротким и его стоимость меньше той, что имелась раньше, то значение заменяется и отметается предыдущая ветвь поиска. Для примера, на карте вы можете рассмотреть узел B, который является одновременно дочерним для узлов из множества ветвей дерева поиска. Соответственно, значение его стоимости при каждом расчете нужно сравнивать с уже имеющимся.
Таким образом, искомого результата в нашем примере мы можем достичь сразу несколькими алгоритмическими моделями:
. поиск в глубину с помощью рекурсии до 9 уровня*;
. поиск в глубину с помощью рекурсии до 9 уровня с оптимизацией, исключающей расчеты цикличных ветвей. В более сложных задачах такая оптимизация может уменьшить количество расчетов по экспоненциальному закону, то есть значительно;
. поиск в ширину до 9 уровня*;
. поиск в ширину по стоимости с оптимизацией, исключающей расчеты цикличных ветвей. То есть, нужно выделить только перспективные ветви; . Graph-Search, то есть Tree-Search с закрытым и открытым списками.
* — обратите внимание, что, взяв в учет глубину 9, мы предусмотрели вариант перебора всех возможных решений, но… посмотрев на карту, вы можете без труда увидеть, что нужное нам находится уже на третьем уровне.
В данном случае мы рассмотрели варианты неинформированного поиска, при котором результат ищется в рамках данных, которые представлены в описании задачи, и предметная область не расматривается. По существу, можно получить конкретный ответ о том, достигнута цель или нет, но при этом не используются методы выявления наибольшей вероятности нахождения оптимального решения, выбора нужной ветки и так далее.
Чтобы легче было понять сказанное, рассмотрим следующий пример.
А*-поиск
Нужно отметить, что сам алгоритм весьма прост как в объяснении, так и в реализации, хотя стоит отметить несколько его разновидностей, которые применимы или нет в зависимости от сложности и специфики поставленной задачи.
Мы же сейчас рассмотрим самый простейший пример на небольшой игровой карте. Допустим, наш персонаж должен добраться с клетки А на клетку B по кратчайшему пути, обогнув небольшое препятствие, причем упростим задачу до того, что он может двигаться только по вертикали и горизонтали. Каждая из клеток в данном случае и будет являться узлом. Для начала отправную клетку (корневой узел) заносим в закрытый список, при этом видим, что герой может идти только по четырем направлениям.
Как мы будем их оценивать и что брать за стоимость? В данном случае вполне достаточно вычислять ее из двух величин:
. расстояние исследуемой клетки от начальной позиции. Высчитывается как сумма клеток по горизонтали и вертикали между отправным пунктом и конкретным узлом;
. расстояние от исследуемой клетки до цели. Высчитывается как сумма клеток по горизонтали и вертикали между конкретным узлом и целью. А суммарная стоимость будет являться суммой этих двух величин. И чем она меньше, тем оптимальнее сам ход (эта сумма показана курсивом). И так вычисляется один узел за другим, с внесением наиболее оптимальных (с наименьшей стоимостью) клеток в закрытый список, пока в открытом списке не появится клетка цели. После этого формируется маршрут.
Как вы могли заметить, на предложенном рисунке две клетки, расположенные возле А, имеют одинаковую стоимость, что может подразумевать некоторые проблемы. На самом деле от них можно избавиться различными путями, например, взять в учет только ту клетку, которая идет первой по открытому списку, либо предусмотреть случайный режим, хотя в реальной практике все несколько и сложнее, и проще одновременно, потому как стоимость каждой клетки может складываться из множества дополнительных составляющих.
***
Возвращаясь к примеру с картой населенных пунктов, можно отметить, что она очень быстро решаема в рамках применения алгоритма A*-поиска, если разместить саму карту на сетке координат. То есть, вычислив суммарную стоимость узлов относительно расстояния от начального пункта следования и от цели, вы без труда получите результат "Мой город" ( D ( E ( "Цель", который и будет являться правильным решением. Причем сам алгоритм будет работать даже в случае, когда, например, между пунктами E и "Цель" отсутствует дорога. Тогда будет успешно рассчитан другой маршрут, и он будет наиболее коротким. Проблемы могут возникнуть в случаях, когда дороги не являются ровными, и, например, расстояние DE будет большим, чем DG. В данном случае сетка координат с населенными пунктами не поможет, и нужно предусматривать более сложные варианты, например с разбиением на большее количество узлов.
Абстрагирование
На самом деле одним из ключевых моментов при постановке задачи поиска является отделение зерен от плевел, другими словами, абстрагирование. То есть выдача только необходимых и оптимальных данных при описании задания.
Допустим, в населенном пункте B находится красивый замок, и путешественник хочет его обязательно посетить. Таким образом, нужно составить другой оптимальный маршрут и при стоимости узлов для поиска учитывать данный момент. Также на карте вы можете найти два места — "грязь" и "проселочная дорога", которые при определенных обстоятельствах нужно учитывать в стоимости. Но если человеку все равно, увидит он этот замок или нет, то такая информация будет абсолютно ненужной, как, например, для составления маршрута все равно, какой будет вид из окна, если это не входит в требуемые условия задачи. И особенно важно это при постановке задач для неинформированного поиска.
Кристофер christopher@tut.by
Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике технологии
