3D во Flash: играем в конструктор
3D во Flash: играем в конструктор
Эффект, который мы создадим, будет действительно необычен. Это будет куб, составленный из маленьких кубиков. "Ну и что, — скажете вы, — я нарисую такой объект за одну минуту". Да, действительно, не надо быть корифеем во Flash, чтобы изобразить подобную геометрическую фигуру. Но наш куб будет с секретом! При щелчке по любому из составляющих его кубиков последний будет исчезать. Используя это, можно будет получить из куба, например, пирамиду. Интересно? Тогда — вперед.
Flash не предоставляет абсолютно никаких специализированных инструментов для создания трехмерной графики. Любые объекты в нем двухмерны и, соответственно, обладают лишь двумя координатами — x и y — и двумя пространственными характеристиками — шириной и высотой. Как при этом возможно создать трехмерный объект?
Да, задача, конечно, не из самых простых. Но она вполне решаема! Чтобы это понять, вспомните, что в компьютере изначально заложена только двухмерная система координат: это горизонталь и вертикаль монитора. И между тем существуют такие великолепные программы, как 3D-max или Bruce 3D, позволяющие создавать абсолютно реалистичные изображения пространственных объектов. Но как это им удается, если средства, которыми обладали их создатели, ничем не шире наших?
Чтобы ответить на этот вопрос, нужно понять, что мы на самом деле не видим объема окружающего нас мира. Воспринимаемые нами "картинки" — это лишь проекции реальной действительности на плоскость нашего зрения. И — не более того. Эффект же объемности создается перспективой и игрой светотени. Именно поэтому художникам так просто удается повторять трехмерную реальность на плоских холстах.
Почему картины средневековья кажутся плоскими и нереалистичными, а полотна эпохи классицизма очень и очень похожи на фотографии? Ведь изображают они, в принципе, одинаковые вещи. Дело в том, что ранние мастера плохо владели законами перспективы: оттого их творения и кажутся сейчас примитивными. Нужно понимать, почему дом, стоящий в ста метрах от наблюдателя, будет казаться меньше более близкого и почему боковая сторона куба должна быть нарисована меньшей по сравнению с центральной. Ответы на все эти вопросы даются в теории перспективы и отчасти геометрической оптики. "Говорят" же эти науки на языке математики, а точнее, геометрии.
Как создаются трехмерные объекты, например, в Bruce? В принципе, так же, как двухмерные во Flash. Описываются положения узловых точек кривых, цвет заливок и распределение источников освещения.
Но все это делается в памяти компьютера — ведь, как вы помните, трехмерных изображений быть не может. Перед отображением же на экран выполняется проецирование с учетом всех необходимых искажений и прорисовкой теней.
Делаем вывод. Трехмерный мир объективно существует, но видим мы лишь его проекцию. Поэтому, чтобы создать трехмерный эффект во Flash, мы должны описать поведение объектов как пространственное, а затем в нужный момент спроецировать его на плоскость. Четкое понимание этого принципа позволяет делать многие удивительные вещи.
Однако теория без практики мертва, поэтому приступим к созданию задуманного эффекта.
Для начала мы должны нарисовать сам кубик. Для этого нужно решить, как будут расположены оси системы координат. Наиболее простым вариантом с точки зрения потребующегося затем (например, для проецирования) математического аппарата является система координат, показанная на рис. 1, так как две из трех ее осей совпадают с осями фильма Flash.
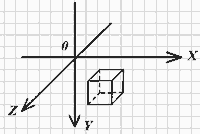
Рис. 1. Система координат
Пускай для определенности ребро кубика будет равно 20 пикселям. Тогда какой длины должны быть нарисованы параллельные плоскости ZOY ребра? Тоже 20 пикселей? В самом деле, отчего бы и нет, если все ребра равны, а оси перпендикулярны... Пробуем нарисовать куб исходя из этого предположения.
Линия, линия, линия. Заливка, заливка, заливка. И получается... параллелепипед! Да, в чем-то мы явно ошиблись (рис. 2 (вариант a)).
Дело в том, что ось Z на приведенном рисунке является проекцией "настоящей" Z на плоскость, составляющую 45° с предполагаемым направлением взгляда. Подобное искажение весьма искусственно, но без него невозможно было показать объем: если бы все было "честно", то при параллельности Z направлению взгляда мы бы видели только переднюю грань. Более точно можно было бы отобразить куб, если бы сама система координат повернулась на 45°. Но, пожалуй, описать подобное преобразование будет слишком сложно.
Итак, если ось на самом деле не ось, а проекция, то соответствующим образом должны быть изменены и все рассматриваемые относительно нее объекты. Поэтому, чтобы узнать видимую длину ребра, нужно умножить реальный его размер на косинус угла проецирования (он равен 45°).
trace(20*Math.cos(Math.PI/4)); // Выводит: 14.142135623731
trace(20*Math.SQRT1_2); // Выводит: 14.142135623731 (косинус от 45* равен 1/21/2)
Таким образом, длина боковых ребер должна быть меньше длины передних и составлять приблизительно 14 пикселей. Зная это, рисуем кубик.
Советы:
• Включите вспомогательную сетку (команда Grid(Show Grid) контекстного меню рабочего поля). Чтобы размеры ее ячейки совпадали с параметрами грани куба, задайте их самостоятельно, воспользовавшись командой Edit Grid контекстного меню.
• Рисуйте в масштабе не менее 200%.
• Чтобы нарисовать боковые ребра, действуйте следующим образом:
• Рисуете при помощи инструмента Line (Линия) горизонтальный отрезок произвольной длины (чтобы он получился ровным, держите зажатой клавишу <Shift> ).
• В окошке width панели Properties (Свойства) меняете величину его ширины на 14.
• Чтобы повернуть отрезок на 45°, воспользуйтесь инструментом Free Transform (Свободная трансформация) при нажатой клавише <Shift> .
• Создайте две копии нарисованного отрезка.
• Размещая ребра, перейдите в масштаб 500-800%: эта работа должна быть выполнена предельно точно, иначе кубики не будут плотно прилегать друг к другу.
• Залить грани необходимо оттенками серого так, чтобы правая была освещена в наибольшей, а передняя — в наименьшей степени.
Мы достаточно подробно описали такую, казалось бы, элементарную операцию, как создание кубика, так как от нее зависит успешность всей остальной работы. То, как должен выглядеть кубик, показано на рисунке 2 (вариант b).

Рис. 2. Кубики
Переводим кубик в клип (F8), назвав его kubik. В качестве идентификатора для ActionScript-экспорта задаем слово "cub".
Как мы будем строить большой куб? Очевидно, так же, как складывается стена из кирпичей: кубик добавляем к кубику, пока не закончится рядок. Переходим к новому рядку и все повторяем заново. Когда завершается слой, начинаем новый и проделываем те же действия, что и на предыдущем.
Промоделировать описанный алгоритм можно, задав три вложенных цикла. Верхний будет отвечать за слои, средний — за рядки, нижний — за отдельные кубики в рядках. Соответственно первый будет менять координаты по Z, второй — по Y, третий — по X (другие варианты также возможны).
Пусть большой куб будет образован 5*5*5=125 маленькими кубиками:
for (var i = 0; i<5; i++) {
for (var j = 0; j<5; j++) {
for (var k = 0; k<5; k++) {
}}}
Когда придет время разместить новый куб, прежде всего, должен быть создан очередной экземпляр клипа kubik:
Arr[n]=attachMovie("cub","cub",n);
n++;
В приведенном коде есть два не оговаривавшихся нами элемента:
— Переменная n. Является счетчиком, определяющим порядковый номер созданного кубика. При помощи нее мы задаем глубину объекта (введенные раньше кубики должны отображаться ниже, чем их более "молодые" коллеги), а также его индекс в массиве Arr. Вместо n можно использовать и выражение из переменных циклов (n=25*i + 5*j + k). Переменная n должна быть задана вне циклов как 0. Операция инкрементирования n должна располагаться всегда ниже всего остального кода в блоке цикла.
— Массив Arr. В нем мы будем хранить все 125 кубиков. Это куда удобнее (и экономичнее с точки зрения ресурсов компьютера), чем использование функции eval(). Кроме того, многие из задач, которые элементарно решаются при помощи массивов, становятся сверхтрудными при программировании без них. Задать пустой массив надо выше циклов:
Arr=[];
Когда кубик будет создан, необходимо вычислить положенные для него координаты.
Если считать, что большой куб располагается по центру рабочей области, то отсчет координат составляющих его кубиков нужно начать со значений X=150, Y=150, Z=0.
Координата по X текущего экземпляра может быть высчитана как произведение длины ребра кубика на количество уже имеющихся в рядке "кирпичиков" (переменная внутреннего цикла k) плюс значение соответствующей координаты точки отсчета:
var X=150+20*k;
Координату по Y можно определить, отняв (с учетом выбранного направления оси) от ее начальной величины произведение числа заполненных рядков в слое (переменная среднего цикла j) на высоту рядка:
var Y=150-20*j;
Аналогично двум предыдущим координатам высчитывается и Z. Однако в ее случае нужно помнить, что мы имеем дело не с самой осью, а с ее проекцией. Поэтому длину ребра нужно дополнительно умножить на корень из двух:
var Z=20*Math.SQRT1_2*i;
Итак, расположение кубиков в пространстве мы описали. Но фильм Flash имеет только две координаты, за которые отвечают свойства _x и _y. Следовательно, мы должны спроецировать координату z на оси X и Y. Но как это сделать?
Для того чтобы ответить на этот вопрос, взглянем на нашу систему координат после проецирования на плоскость (рис. 3).
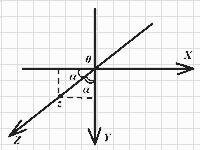
Рис. 3. Спроецированная система координат
Очевидно, что, если точка имеет координаты X=0, Y=0, Z=Z0, то при проецировании ее на плоскость зрения ей будут соответствовать координаты x=-Z0*cos(45*) и y= Z0*cos(45*) (исходя из рисунка 3). Из этого следует, что, если проецируется точка с координатами X=X0, Y=Y0, Z=Z0, то видеть ее мы будем в положении x=X0- Z0*cos(45*) и y=Y0 + Z0*cos(45*).
Исходя из полученных формул должны высчитываться положения кубиков:
Arr[n]._x=X-Z*Math.SQRT1_2;
Arr[n]._y=Y+Z*Math.SQRT1_2;
Вроде бы, все... С тревогой в сердце нажимаем <Ctrl> +<Enter> . Неужели не получится? Неужели в своих рассуждениях мы были не правы?.. Ура! Работает! (см. рис. 4).

Рис. 4. Собранный кубик
Изображением кубика трудно кого-то удивить. А вот если бы можно было щелчком мыши удалять любой из его кирпичиков, создавая тем самым более сложные геометрические фигуры — вот это было бы интересно. Но как это сделать?
Можно поступить так: при наступлении события onMouseDown запускать цикл и проверять, что возвращает метод hitTest для каждого из экземпляров. Правда, в данном случае нужно было бы "прочесывать" массив с конца, так как должен быть убран тот из находившихся под указателем мыши во время щелчка экземпляров, который расположен выше всех остальных. Однако такой подход нельзя назвать техничным ввиду громоздкости его кода и большого количества лишних операций.
Подумайте, как все было бы просто, если бы наши кубики относились к классу Button. Достаточно было бы просто создать для каждого из них обработчик события onPress, содержащий в блоке удаляющий объект код. Но клипы — это, увы, не кнопки...
Да, клипы — это не кнопки, но во Flash MX Macromedia немало облегчила труд разработчиков, сделав "кнопочные" события "родными" и для класса MovieClip. То есть сейчас события onPress, onRelease, onRollOut, onRollOver, onDragOut, onDrag Over "слушаются" и клипами точно так же, как, например, onEnterFrame. И это существенно облегчает нашу задачу.
Однако тут же возникает вопрос: мы же не можем создать отдельный обработчик для каждого из 125 экземпляров? Можно ли как-то "сказать" всем кубикам сразу, что при щелчке по одному из них он должен исчезнуть?
Кубики — это братья-близнецы. Более того: они даже ближе, поскольку, по сути, являются лишь ссылками на клип в библиотеке. А что, если "повесить" код на временную шкалу этого клипа? Тогда ему будут следовать все его экземпляры.
Остается нерешенной одна техническая деталь. Как указать обработчику, что он должен "слушать" события именно того экземпляра, на временной шкале которого он "висит". А сделать это можно очень просто, использовав предложение this. Его особенность заключается в том, что оно всегда возвращает адрес той временной шкалы, на которой находится:
trace(this); // Выводит: _level0 (код введен на первый кадр основной временной шкалы)
Получить адрес временной шкалы, на которой располагается данный экземпляр, можно использовав схожее с this свойство _parent:
trace(_parent); // Выводит: _level0 (код введен на первый кадр клипа kubik)
Код, который нужно ввести на первый кадр расположенного в библиотеке клипа kubik, должен выглядеть как:
this.onPress = function() {
this.removeMovieClip();
}
Тестируем фильм. Все получилось! Кубики действительно убираются так, как будто фигура объемная. Светотень же столь естественна, что это даже удивляет. Немного пощелкав по кубу, можно получить самую необычную фигуру (рис. 5).
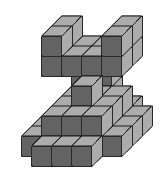
Рис. 5. Фигура, полученная из куба
Замечательно! Только вот, правда, мы нарушили один очень важный принцип: весь код должен быть в одном месте (то есть централизован). Но как можно создать обработчик, действующий на все кубики, не "вешая" его на символ в библиотеке?
Экземпляры наследуют свойства символа. Символ в свою очередь наследует свойства и методы класса MovieClip. А нельзя ли каким-то образом сделать функцию-обработчик присущей сразу всему классу? Да, это возможно. Для этого нужно использовать особый оператор prototype:
MovieClip.prototype.onPress=function(){
this.removeMovieClip();
}
Добавив этот код к остальному, мы получим тот же результат, что и при размещении обработчика на временной шкале клипа в библиотеке.
Продемонстрированный ход эффективен, так как, кроме кубиков, в нашем фильме нет других клипов. А если бы они были — ведь они бы тоже исчезали при щелчке по ним?
В том случае, если бы на поле присутствовали другие клипы, которые не должны были бы реагировать на щелчок мышью, мы создали бы новый подкласс на основе MovieClip и сделали кубики его объектами.
При этом мы могли бы "повесить" на него функцию, аналогичную приведенной выше, не изменив поведение остальных клипов. В самом деле — возможности объектно-ориентированного программирования в ActionScript очень широки. Если вы заинтересуетесь им, изучите материалы на сайте http://de-breuil.flashmaster.ru/ch01_Arguments.htm .
Как только мы начали "слушать" кнопочные события, при наведении указателя мыши на кубики его вид стал меняться со стрелки на руку. Чтобы это изменение не происходило, обратимся к отвечающему за него свойству класса MovieClip useHandCursor. В блок циклов (выше инкрементирования n) введите:
Arr[n].useHandCursor=false;
Было бы замечательно, если бы в начале работы фильма куб собирался из кирпичиков на глазах у пользователя. Но замедлить цикл невозможно, а переписывать код не очень хочется. Мы поступим по-другому. Куб будет создаваться, как и раньше, почти мгновенно — но из невидимых кирпичиков. Затем же мы будем просто "включать" их в нужной нам последовательности с подходящей частотой.
Чтобы все кубики стали невидимыми, введите в цикл:
Arr[n]._visible=false;
Частоту вызовов функции, визуализирующей кубики, мы можем связать с событием onEnterFrame. Но это не слишком рационально, так как не позволяет менять ее значение в ходе работы фильма, а также связано с излишней вычислительной работой тогда, когда все кубики станут видимыми. Гораздо лучше воспользоваться нововведением Flash MX — функцией setTransform().
Функция setTransform(functionName,Time,{par}), где functionName — имя вызываемой функции, Time — частота вызовов в миллисекундах, par — список передаваемых параметров, предназначена для периодических вызовов некоторой функции с произвольной частотой. Ее появление во Flash MX — это одно из наиболее полезных новшеств, так как оно избавляет от жесткой привязки к частоте кадров фильма.
В нашем случае в секунду должно появляться 10 кубиков:
// Код нужно разместить строго ниже циклов
TIME=setInterval(Visual,100);
function Visual(){
var t=Math.round(Math.random()* Arr.length);
Arr[t]._visible=true;
}
Чтобы скорость появления кубиков не зависела от количества уже видимых "кирпичиков", "включенный" экземпляр должен удаляться из массива Arr:
Arr.splice(t,1);
Когда все кубики станут видимыми, вызовы функции Visual() должны прекратиться. Отключить работу setInterval() можно при помощи функции clearInterval (Interv), где Interv — хранящая таймер переменная.
Добавьте в функцию Visual() следующий код:
if(Arr.length==1){
clearInterval(TIME);
}

Рис. 6. Кубик на этапе сборки
Вот и все. Замечательный эффект готов! При желании вы без труда напишете к нему интерфейс, при помощи которого пользователь сможет задавать число кубиков вдоль каждой из осей, а также начинать сборку заново. Домашним же заданием будет следующее: попробуйте написать аналогичную программу, но организующую шарики в большой шар. Это куда сложнее и будет хорошей проверкой ваших способностей.
Дмитрий Гурский,
Юрий Стрельченко, dot@omen.ru
Эффект, который мы создадим, будет действительно необычен. Это будет куб, составленный из маленьких кубиков. "Ну и что, — скажете вы, — я нарисую такой объект за одну минуту". Да, действительно, не надо быть корифеем во Flash, чтобы изобразить подобную геометрическую фигуру. Но наш куб будет с секретом! При щелчке по любому из составляющих его кубиков последний будет исчезать. Используя это, можно будет получить из куба, например, пирамиду. Интересно? Тогда — вперед.
Flash не предоставляет абсолютно никаких специализированных инструментов для создания трехмерной графики. Любые объекты в нем двухмерны и, соответственно, обладают лишь двумя координатами — x и y — и двумя пространственными характеристиками — шириной и высотой. Как при этом возможно создать трехмерный объект?
Да, задача, конечно, не из самых простых. Но она вполне решаема! Чтобы это понять, вспомните, что в компьютере изначально заложена только двухмерная система координат: это горизонталь и вертикаль монитора. И между тем существуют такие великолепные программы, как 3D-max или Bruce 3D, позволяющие создавать абсолютно реалистичные изображения пространственных объектов. Но как это им удается, если средства, которыми обладали их создатели, ничем не шире наших?
Чтобы ответить на этот вопрос, нужно понять, что мы на самом деле не видим объема окружающего нас мира. Воспринимаемые нами "картинки" — это лишь проекции реальной действительности на плоскость нашего зрения. И — не более того. Эффект же объемности создается перспективой и игрой светотени. Именно поэтому художникам так просто удается повторять трехмерную реальность на плоских холстах.
Почему картины средневековья кажутся плоскими и нереалистичными, а полотна эпохи классицизма очень и очень похожи на фотографии? Ведь изображают они, в принципе, одинаковые вещи. Дело в том, что ранние мастера плохо владели законами перспективы: оттого их творения и кажутся сейчас примитивными. Нужно понимать, почему дом, стоящий в ста метрах от наблюдателя, будет казаться меньше более близкого и почему боковая сторона куба должна быть нарисована меньшей по сравнению с центральной. Ответы на все эти вопросы даются в теории перспективы и отчасти геометрической оптики. "Говорят" же эти науки на языке математики, а точнее, геометрии.
Как создаются трехмерные объекты, например, в Bruce? В принципе, так же, как двухмерные во Flash. Описываются положения узловых точек кривых, цвет заливок и распределение источников освещения.
Но все это делается в памяти компьютера — ведь, как вы помните, трехмерных изображений быть не может. Перед отображением же на экран выполняется проецирование с учетом всех необходимых искажений и прорисовкой теней.
Делаем вывод. Трехмерный мир объективно существует, но видим мы лишь его проекцию. Поэтому, чтобы создать трехмерный эффект во Flash, мы должны описать поведение объектов как пространственное, а затем в нужный момент спроецировать его на плоскость. Четкое понимание этого принципа позволяет делать многие удивительные вещи.
Однако теория без практики мертва, поэтому приступим к созданию задуманного эффекта.
Для начала мы должны нарисовать сам кубик. Для этого нужно решить, как будут расположены оси системы координат. Наиболее простым вариантом с точки зрения потребующегося затем (например, для проецирования) математического аппарата является система координат, показанная на рис. 1, так как две из трех ее осей совпадают с осями фильма Flash.

Рис. 1. Система координат
Пускай для определенности ребро кубика будет равно 20 пикселям. Тогда какой длины должны быть нарисованы параллельные плоскости ZOY ребра? Тоже 20 пикселей? В самом деле, отчего бы и нет, если все ребра равны, а оси перпендикулярны... Пробуем нарисовать куб исходя из этого предположения.
Линия, линия, линия. Заливка, заливка, заливка. И получается... параллелепипед! Да, в чем-то мы явно ошиблись (рис. 2 (вариант a)).
Дело в том, что ось Z на приведенном рисунке является проекцией "настоящей" Z на плоскость, составляющую 45° с предполагаемым направлением взгляда. Подобное искажение весьма искусственно, но без него невозможно было показать объем: если бы все было "честно", то при параллельности Z направлению взгляда мы бы видели только переднюю грань. Более точно можно было бы отобразить куб, если бы сама система координат повернулась на 45°. Но, пожалуй, описать подобное преобразование будет слишком сложно.
Итак, если ось на самом деле не ось, а проекция, то соответствующим образом должны быть изменены и все рассматриваемые относительно нее объекты. Поэтому, чтобы узнать видимую длину ребра, нужно умножить реальный его размер на косинус угла проецирования (он равен 45°).
trace(20*Math.cos(Math.PI/4)); // Выводит: 14.142135623731
trace(20*Math.SQRT1_2); // Выводит: 14.142135623731 (косинус от 45* равен 1/21/2)
Таким образом, длина боковых ребер должна быть меньше длины передних и составлять приблизительно 14 пикселей. Зная это, рисуем кубик.
Советы:
• Включите вспомогательную сетку (команда Grid(Show Grid) контекстного меню рабочего поля). Чтобы размеры ее ячейки совпадали с параметрами грани куба, задайте их самостоятельно, воспользовавшись командой Edit Grid контекстного меню.
• Рисуйте в масштабе не менее 200%.
• Чтобы нарисовать боковые ребра, действуйте следующим образом:
• Рисуете при помощи инструмента Line (Линия) горизонтальный отрезок произвольной длины (чтобы он получился ровным, держите зажатой клавишу <Shift> ).
• В окошке width панели Properties (Свойства) меняете величину его ширины на 14.
• Чтобы повернуть отрезок на 45°, воспользуйтесь инструментом Free Transform (Свободная трансформация) при нажатой клавише <Shift> .
• Создайте две копии нарисованного отрезка.
• Размещая ребра, перейдите в масштаб 500-800%: эта работа должна быть выполнена предельно точно, иначе кубики не будут плотно прилегать друг к другу.
• Залить грани необходимо оттенками серого так, чтобы правая была освещена в наибольшей, а передняя — в наименьшей степени.
Мы достаточно подробно описали такую, казалось бы, элементарную операцию, как создание кубика, так как от нее зависит успешность всей остальной работы. То, как должен выглядеть кубик, показано на рисунке 2 (вариант b).

Рис. 2. Кубики
Переводим кубик в клип (F8), назвав его kubik. В качестве идентификатора для ActionScript-экспорта задаем слово "cub".
Как мы будем строить большой куб? Очевидно, так же, как складывается стена из кирпичей: кубик добавляем к кубику, пока не закончится рядок. Переходим к новому рядку и все повторяем заново. Когда завершается слой, начинаем новый и проделываем те же действия, что и на предыдущем.
Промоделировать описанный алгоритм можно, задав три вложенных цикла. Верхний будет отвечать за слои, средний — за рядки, нижний — за отдельные кубики в рядках. Соответственно первый будет менять координаты по Z, второй — по Y, третий — по X (другие варианты также возможны).
Пусть большой куб будет образован 5*5*5=125 маленькими кубиками:
for (var i = 0; i<5; i++) {
for (var j = 0; j<5; j++) {
for (var k = 0; k<5; k++) {
}}}
Когда придет время разместить новый куб, прежде всего, должен быть создан очередной экземпляр клипа kubik:
Arr[n]=attachMovie("cub","cub",n);
n++;
В приведенном коде есть два не оговаривавшихся нами элемента:
— Переменная n. Является счетчиком, определяющим порядковый номер созданного кубика. При помощи нее мы задаем глубину объекта (введенные раньше кубики должны отображаться ниже, чем их более "молодые" коллеги), а также его индекс в массиве Arr. Вместо n можно использовать и выражение из переменных циклов (n=25*i + 5*j + k). Переменная n должна быть задана вне циклов как 0. Операция инкрементирования n должна располагаться всегда ниже всего остального кода в блоке цикла.
— Массив Arr. В нем мы будем хранить все 125 кубиков. Это куда удобнее (и экономичнее с точки зрения ресурсов компьютера), чем использование функции eval(). Кроме того, многие из задач, которые элементарно решаются при помощи массивов, становятся сверхтрудными при программировании без них. Задать пустой массив надо выше циклов:
Arr=[];
Когда кубик будет создан, необходимо вычислить положенные для него координаты.
Если считать, что большой куб располагается по центру рабочей области, то отсчет координат составляющих его кубиков нужно начать со значений X=150, Y=150, Z=0.
Координата по X текущего экземпляра может быть высчитана как произведение длины ребра кубика на количество уже имеющихся в рядке "кирпичиков" (переменная внутреннего цикла k) плюс значение соответствующей координаты точки отсчета:
var X=150+20*k;
Координату по Y можно определить, отняв (с учетом выбранного направления оси) от ее начальной величины произведение числа заполненных рядков в слое (переменная среднего цикла j) на высоту рядка:
var Y=150-20*j;
Аналогично двум предыдущим координатам высчитывается и Z. Однако в ее случае нужно помнить, что мы имеем дело не с самой осью, а с ее проекцией. Поэтому длину ребра нужно дополнительно умножить на корень из двух:
var Z=20*Math.SQRT1_2*i;
Итак, расположение кубиков в пространстве мы описали. Но фильм Flash имеет только две координаты, за которые отвечают свойства _x и _y. Следовательно, мы должны спроецировать координату z на оси X и Y. Но как это сделать?
Для того чтобы ответить на этот вопрос, взглянем на нашу систему координат после проецирования на плоскость (рис. 3).

Рис. 3. Спроецированная система координат
Очевидно, что, если точка имеет координаты X=0, Y=0, Z=Z0, то при проецировании ее на плоскость зрения ей будут соответствовать координаты x=-Z0*cos(45*) и y= Z0*cos(45*) (исходя из рисунка 3). Из этого следует, что, если проецируется точка с координатами X=X0, Y=Y0, Z=Z0, то видеть ее мы будем в положении x=X0- Z0*cos(45*) и y=Y0 + Z0*cos(45*).
Исходя из полученных формул должны высчитываться положения кубиков:
Arr[n]._x=X-Z*Math.SQRT1_2;
Arr[n]._y=Y+Z*Math.SQRT1_2;
Вроде бы, все... С тревогой в сердце нажимаем <Ctrl> +<Enter> . Неужели не получится? Неужели в своих рассуждениях мы были не правы?.. Ура! Работает! (см. рис. 4).

Рис. 4. Собранный кубик
Изображением кубика трудно кого-то удивить. А вот если бы можно было щелчком мыши удалять любой из его кирпичиков, создавая тем самым более сложные геометрические фигуры — вот это было бы интересно. Но как это сделать?
Можно поступить так: при наступлении события onMouseDown запускать цикл и проверять, что возвращает метод hitTest для каждого из экземпляров. Правда, в данном случае нужно было бы "прочесывать" массив с конца, так как должен быть убран тот из находившихся под указателем мыши во время щелчка экземпляров, который расположен выше всех остальных. Однако такой подход нельзя назвать техничным ввиду громоздкости его кода и большого количества лишних операций.
Подумайте, как все было бы просто, если бы наши кубики относились к классу Button. Достаточно было бы просто создать для каждого из них обработчик события onPress, содержащий в блоке удаляющий объект код. Но клипы — это, увы, не кнопки...
Да, клипы — это не кнопки, но во Flash MX Macromedia немало облегчила труд разработчиков, сделав "кнопочные" события "родными" и для класса MovieClip. То есть сейчас события onPress, onRelease, onRollOut, onRollOver, onDragOut, onDrag Over "слушаются" и клипами точно так же, как, например, onEnterFrame. И это существенно облегчает нашу задачу.
Однако тут же возникает вопрос: мы же не можем создать отдельный обработчик для каждого из 125 экземпляров? Можно ли как-то "сказать" всем кубикам сразу, что при щелчке по одному из них он должен исчезнуть?
Кубики — это братья-близнецы. Более того: они даже ближе, поскольку, по сути, являются лишь ссылками на клип в библиотеке. А что, если "повесить" код на временную шкалу этого клипа? Тогда ему будут следовать все его экземпляры.
Остается нерешенной одна техническая деталь. Как указать обработчику, что он должен "слушать" события именно того экземпляра, на временной шкале которого он "висит". А сделать это можно очень просто, использовав предложение this. Его особенность заключается в том, что оно всегда возвращает адрес той временной шкалы, на которой находится:
trace(this); // Выводит: _level0 (код введен на первый кадр основной временной шкалы)
Получить адрес временной шкалы, на которой располагается данный экземпляр, можно использовав схожее с this свойство _parent:
trace(_parent); // Выводит: _level0 (код введен на первый кадр клипа kubik)
Код, который нужно ввести на первый кадр расположенного в библиотеке клипа kubik, должен выглядеть как:
this.onPress = function() {
this.removeMovieClip();
}
Тестируем фильм. Все получилось! Кубики действительно убираются так, как будто фигура объемная. Светотень же столь естественна, что это даже удивляет. Немного пощелкав по кубу, можно получить самую необычную фигуру (рис. 5).

Рис. 5. Фигура, полученная из куба
Замечательно! Только вот, правда, мы нарушили один очень важный принцип: весь код должен быть в одном месте (то есть централизован). Но как можно создать обработчик, действующий на все кубики, не "вешая" его на символ в библиотеке?
Экземпляры наследуют свойства символа. Символ в свою очередь наследует свойства и методы класса MovieClip. А нельзя ли каким-то образом сделать функцию-обработчик присущей сразу всему классу? Да, это возможно. Для этого нужно использовать особый оператор prototype:
MovieClip.prototype.onPress=function(){
this.removeMovieClip();
}
Добавив этот код к остальному, мы получим тот же результат, что и при размещении обработчика на временной шкале клипа в библиотеке.
Продемонстрированный ход эффективен, так как, кроме кубиков, в нашем фильме нет других клипов. А если бы они были — ведь они бы тоже исчезали при щелчке по ним?
В том случае, если бы на поле присутствовали другие клипы, которые не должны были бы реагировать на щелчок мышью, мы создали бы новый подкласс на основе MovieClip и сделали кубики его объектами.
При этом мы могли бы "повесить" на него функцию, аналогичную приведенной выше, не изменив поведение остальных клипов. В самом деле — возможности объектно-ориентированного программирования в ActionScript очень широки. Если вы заинтересуетесь им, изучите материалы на сайте http://de-breuil.flashmaster.ru/ch01_Arguments.htm .
Как только мы начали "слушать" кнопочные события, при наведении указателя мыши на кубики его вид стал меняться со стрелки на руку. Чтобы это изменение не происходило, обратимся к отвечающему за него свойству класса MovieClip useHandCursor. В блок циклов (выше инкрементирования n) введите:
Arr[n].useHandCursor=false;
Было бы замечательно, если бы в начале работы фильма куб собирался из кирпичиков на глазах у пользователя. Но замедлить цикл невозможно, а переписывать код не очень хочется. Мы поступим по-другому. Куб будет создаваться, как и раньше, почти мгновенно — но из невидимых кирпичиков. Затем же мы будем просто "включать" их в нужной нам последовательности с подходящей частотой.
Чтобы все кубики стали невидимыми, введите в цикл:
Arr[n]._visible=false;
Частоту вызовов функции, визуализирующей кубики, мы можем связать с событием onEnterFrame. Но это не слишком рационально, так как не позволяет менять ее значение в ходе работы фильма, а также связано с излишней вычислительной работой тогда, когда все кубики станут видимыми. Гораздо лучше воспользоваться нововведением Flash MX — функцией setTransform().
Функция setTransform(functionName,Time,{par}), где functionName — имя вызываемой функции, Time — частота вызовов в миллисекундах, par — список передаваемых параметров, предназначена для периодических вызовов некоторой функции с произвольной частотой. Ее появление во Flash MX — это одно из наиболее полезных новшеств, так как оно избавляет от жесткой привязки к частоте кадров фильма.
В нашем случае в секунду должно появляться 10 кубиков:
// Код нужно разместить строго ниже циклов
TIME=setInterval(Visual,100);
function Visual(){
var t=Math.round(Math.random()* Arr.length);
Arr[t]._visible=true;
}
Чтобы скорость появления кубиков не зависела от количества уже видимых "кирпичиков", "включенный" экземпляр должен удаляться из массива Arr:
Arr.splice(t,1);
Когда все кубики станут видимыми, вызовы функции Visual() должны прекратиться. Отключить работу setInterval() можно при помощи функции clearInterval (Interv), где Interv — хранящая таймер переменная.
Добавьте в функцию Visual() следующий код:
if(Arr.length==1){
clearInterval(TIME);
}

Рис. 6. Кубик на этапе сборки
Вот и все. Замечательный эффект готов! При желании вы без труда напишете к нему интерфейс, при помощи которого пользователь сможет задавать число кубиков вдоль каждой из осей, а также начинать сборку заново. Домашним же заданием будет следующее: попробуйте написать аналогичную программу, но организующую шарики в большой шар. Это куда сложнее и будет хорошей проверкой ваших способностей.
Дмитрий Гурский,
Юрий Стрельченко, dot@omen.ru
Компьютерная газета. Статья была опубликована в номере 05 за 2003 год в рубрике soft :: графика


