Долговечность железобетонных конструкций при воздействии коррозии арматуры
Три последних десятилетия исследования коррозии арматуры в бетоне были весьма интенсивными: Tonini и Dean /1/, ACI C222 /2/, Schiessl /3/, Berke /4/, Andrade /5, 6/. Тем не менее, изучение последних публикаций - Bamforth (1999 г.) /7/, De Scutter (1999 г.) /8/, Yoon (1999 г.), Otsuki (2000 г.) /9/, Roberts (2000 г.) /10/, Francois и Casteel (2001 г.) /11/ и проектов вновь вводимых стандартов по бетону (BS8500 и EN206) - свидетельствует о том, что современное состояние науки о процессах коррозии и, что наиболее важно, об их воздействии на сопротивление конструкции остается неудовлетворительным. Воздействие коррозии арматуры на снижение сопротивления конструкции определяется комплексом факторов /5, 6, 9, 12/. Для железобетонных конструкций с трещинами, возникшими в результате загружения, при постоянном проникновении хлоридов инициирование коррозии арматуры в устье трещин происходит в течение короткого срока службы /9, 11, 13, 14/. Характер развития этой локальной коррозии, результатом которой является продольное трещинообразование в бетоне и предельное снижение сопротивляемости конструкции в терминах прочности и срока службы, имеет важное практическое значение. Исследования этого сложного явления необходимы для понимания самого процесса коррозии и его влияния на сопротивление конструкции. На основе этого строится рациональная модель разрушения конструкции. Цель этой статьи обосновать концепцию оценки качества по сроку службы железобетонных конструкций на примере изгибаемых железобетонных элементов с корродирующей арматурой в результате насыщения хлоридами или карбонизации.
Модель разрушения и функции деструкции
Распространение коррозии приводит к снижению несущей способности конструкции, и поэтому в наибольшей степени интересует инженеров-конструкторов. Предлагаемая модель строится на вероятностной основе. Для оценки каждого жизненного цикла, как показано на рис. 1, необходимо установить обоснованный критерий качества:
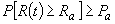
где: P - вероятность события, R(t) - сопротивление конструкции, изменяемое со временем t, т.е. снижение, а - принятое минимальное сопротивление, Pa- принятая минимальная вероятность конструкционной надежности (безопасности).
Как предложено Li, общая модель деструкции может быть в форме
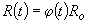
где: j (t) - функция деструкции, Ro- первоначальная несущая способность.
Одним из преимуществ модели деструкции в форме выражения (2) является то, что функция деструкции j является относительной величиной, т.е.:
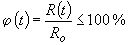
Относительная форма функции деструкции позволяет нормализовать данные экспериментальных исследований конструкций различного типа и первоначальной прочности. Это позволяет максимально использовать имеющиеся экспериментальные данные. С введением функции деструкции выражение (1) принимает вид:
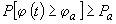
где: ja- принятый предел функции деструкции.
Для данного выражения момент времени, когда выражение (4) не удовлетворяется, является завершением одного жизненного цикла и началом следующего. Следовательно, выражение (4) может использоваться для определения каждого жизненного цикла подверженных коррозии железобетонных конструкций при наличии функции деструкции. Сложность процессов разрушения железобетонных конструкций и распространения коррозии в бетоне и ее воздействия на снижение несущей способности ограничивают развитие сложных аналитических моделей деструкции конструкций, основанных только на теории. Рациональным является развитие эмпирических моделей снижения несущей способности, основанных на экспериментальных данных.
Жизненный цикл определяется как период времени в течение полного срока службы, по окончанию которого требуются мероприятия по содержанию или ремонту железобетонных конструкций, подверженных коррозии арматуры под воздействием хлоридов или при карбонизации. Жизненные циклы характеризуются критериями долговечности и прочности. Первый жизненный цикл подверженных коррозии железобетонных конструкций, как схематически показано на рис. 1, - период времени от завершения возведения конструкций до инициирования коррозии в конструкции - обозначен как (OTi). Этому циклу посвящено большинство исследований в области коррозии арматуры, и поэтому он детально не обсуждается в этой статье /7, 8, 10, 14, 15, 16/. Второй жизненный цикл - период времени от инициирования коррозии до непригодности к эксплуатации конструкции в результате ее воздействия - обозначается как (Ti, Ts). Критериями непригодности к эксплуатации являются трещинообразование бетона в результате коррозии /15, 16, 17, 18/ и прогиб железобетонного элемента. Третий жизненный цикл - период времени от потери пригодности к эксплуатации до окончательного разрушения конструкции - обозначается как (Ts, Tf). Разрушение проявляется по потере прочности на изгиб, на срез и т.д. В этой статье разрушение конструкций характеризуется потерей железобетонными элементами прочности на изгиб.
Для прогноза срока службы подвергаемых коррозии железобетонных конструкций более 20 лет существует хорошо известная модель Tuutti /19/. Главное отличие предлагаемой нами модели (рис. 1) - применяемые критерии качества. Это используемые инженерами-конструкторами предельные состояния по прочности и пригодности к эксплуатации. В модели Tuutti для указания срока службы используют степень коррозии. Однако связь степени коррозии с параметрами несущей способности - прочностью и жесткостью - не является прямой, что подтверждено исследованиями Almusallam, Andrade, Frangopol, Yoon, Otsuki, Roberts, Francois и Castel, Li /5, 6, 9, 10, 11, 12, 13, 14, 15-18, 20/. Очевидно, снижение изгибной прочности конструкции происходит под влиянием комбинации факторов, а не только в связи с уменьшением площади поперечного сечения прокорродировавших стержней, хотя последнее тесно связано со степенью коррозии (Andrade /5, 6/, Clewen /21/). Второе отличие в том, что модель Tuutti предполагает длинный начальный период (около 30% от срока службы).
Расчет железобетонного изгибаемого элемента с учетом потери площади поперечного сечения арматуры
Сопротивление изгибаемого железобетонного элемента определяется по формуле (рис. 2):
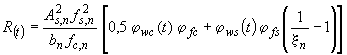
где: Аsn- номинальное значение площади поперечного сечения арматуры (м2),
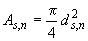
fs,n- номинальное значение предела текучести арматуры (МПа), fc,n- номинальное значение прочности бетона (МПа), bn- номинальное значение ширины поперечного сечения [м],
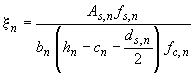
hn- номинальное значение высоты поперечного сечения (м), cn- номинальное значение защитного слоя (мм), ds,n- номинальное значение диаметра арматуры (мм),
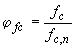
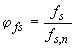
fc- прочность бетона (МПа), fs- предел текучести арматуры (МПа),
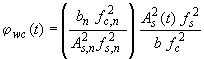
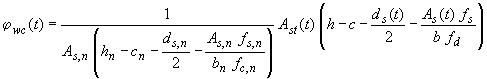
h - высота поперечного сечения, b - ширина поперечного сечения, с - защитный слой бетона, ds(t) - диаметр арматуры, зависящий от времени (м), As(t) - площадь поперечного сечения арматуры, зависящая от времени [м2],
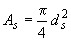
Значения b, c, h, fcи fsварьируются в некотором диапазоне. Размеры показаны на рис. 2. Из формулы (8) видно, что изменение сопротивления R(t) во времени зависит от потери площади поперечного сечения арматуры. Рассмотрены два подхода расчета потери площади поперечного сечения арматуры. Рассмотрена первая коррозионная модель (модель Andrade, рис. 2). Эта одна из наиболее используемых моделей. Потеря диаметра ds(nt) для общей коррозии определяется по формуле:
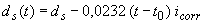
где: icorr- плотность коррозионного тока [mА/см2] (1 m А/см2равен 11,6 мм/год коррозии), t0- время пассивной стадии.
Плотность коррозионного тока icorrи скорость коррозии rcorrизмерялись на реальных конструкциях.
По второй модели коррозии (модель Thoft - Christensen, рис. 2) потеря диаметра ds(t) рассчитывается по формуле
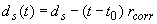
где: rcorr- скорость коррозии (мм/год), t0- время пассивной стадии.
Начало изменения сопротивления во времени зависит от длительности пассивной стадии. Процесс диффузии СО2, например, описывается вторым законом Fick:

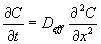
где: С - концентрация агрессивной среды, Deff- коэффициент диффузии.
Используется ряд моделей для расчета пассивной стадии. В первой модели продолжительность пассивной стадии зависит от защитного слоя бетона и константы материала D. Продолжительность пассивной стадии определяется по формуле:
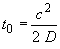
где: D - константа материала.
Вторая модель Frey /32/ более точная, чем первая, но есть ряд трудностей по наличию констант. Глубина слоя карбонизации во времени определяется по формуле:
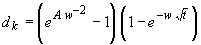
где: А, w - константы, зависящие от условий окружающей среды.
Продолжительность пассивной стадии t = t0рассчитывается из формулы (17), когда dk= с (защитный слой бетона). Значения h, b, c, ds, fc, fs, icorrи в приведенных соотношениях варьируются по закону нормального распределения.
Критическая ширина раскрытия трещины как критерий предельного состояния по долговечности
Критерием предельного состояния по долговечности /15-18/ по предложению автора может служить критическая величина раскрытия продольной трещины в защитном слое бетона, вызванной коррозией арматуры в зоне максимальных напряжений. Таким образом,долговечность железобетонной конструкции есть период ее эксплуатации до достижения предельно допустимой величины раскрытия продольной трещины в защитном слое бетона, вызванной коррозией арматуры в зоне максимальных напряжений, который включает две стадии: а) насыщение хлор-ионами или карбонизация защитного слоя бетона, б) коррозия арматуры при снижении рН среды ниже предела, при котором обеспечивается пассивация поверхностных слоев арматурных стержней.На основании сформулированного определения можно предложить инженерный подход для расчета периода коррозии арматуры. Зафиксирована /34/ линейная зависимость между раскрытием трещины w и коррозией арматуры Δ. Рассматривая защитный слой в виде балочки прямоугольного сечения, нагруженной в пролете и заделанной на опорах, а также считая, что перемещения защитного слоя, отжимаемого корродирующим арматурным стержнем, составляют f = 2Δ /33/, получено выражение (18):
D = wl/8c, (18)
где: l - длина вышла защитного слоя (м), c - толщина защитного слоя (м).
Скорость коррозии или среднюю толщину прокорродировавшего слоя возможно определить, модифицировав формулу Томашова /35/:

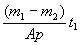
где: т1и m2- масса арматурного стержня до и после коррозии (кг), А - площадь поверхности арматурного стержня (м2), r - плотность металла (кг/м3), t - продолжительность коррозии (годы).
Приравняем выражения (18) и (19):

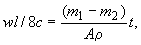
и, введя в формулу обозначение скорости коррозии v, г/(м2, год), преобразуем его относительно >t - времени коррозии арматуры до образования трещины определенной ширины раскрытия:
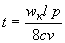
Анализ экспериментальных исследований: снижение прочности и жесткости
Всесторонне проанализирован оригинальный эксперимент, проведенный в университете Данди. Для исследования распространения коррозии арматуры в железобетонных конструкциях и ее воздействия на снижение несущей способности использованы опытные образцы: железобетонные изгибаемые элементы с размерами реальных конструкций. Прочность при изгибе опытных образцов определялась в трех точках в течение испытания, чтобы учесть нелинейный характер при разрушении. Снижение прочности как функция разрушения представлена на рис. 3.
Снижение жесткости конструкционных элементов является важным для оценки разрушения конструкционных систем, т.е. сооружения в целом, поскольку перераспределение нагрузки и, следовательно, тип разрушения зависит от жесткости составляющих его элементов. В эксперименте жесткость образцов оценивалась по прогибу на концах консолей. Оценка жесткости по прогибу имеет преимущества, т.к. включает комбинированный эффект трещинообразования в бетоне и потери сцепления на снижение жесткости. Поскольку жесткость балки обратно пропорциональна ее прогибу, функция разрушения может быть модифицирована в следующем виде:
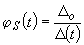
где: Do- начальный предельный прогиб, D(t) - предельный прогиб в момент времени. Снижение жесткости показано на рис. 4.
Снижение прочности железобетонных конструкций в лабораторном эксперименте может быть определено двумя разными методами: испытанием нагружением до разрушения и неразрушающим измерением плотности коррозионного тока. На практике, однако, это возможно только вторым методом. Особенности расчета несущей способности поперечных сечений железобетонных элементов с уменьшенной площадью поперечного сечения представлены в работах Vian /24/, C. Andrade /6/, Jones /25/, Broomfield /26/ и в данной статье. Плотность коррозионного тока icorrне является постоянной, уменьшение площади поперечного сечения прокорродировавших стержней не является линейным. Основываясь на этом, уменьшение прочности нормального сечения опытного образца может быть рассчитано в терминах функции разрушения. На рис. 3 показано для сравнения снижение прочности, определенное испытанием до разрушения. Из этого следует, что метод коррозионного тока значительно недооценивает снижение прочности железобетонных изгибаемых элементов. Максимальная разница в снижении прочности, определенной двумя методами, составляет 22%. Эта разница увеличивается со временем, т.к. сильная коррозия приводит не только к уменьшению площади поперечного сечения, но также является причиной других разрушений нормального сечения. Сравнение на рис. 3 подчеркивает комбинированное воздействие коррозии арматуры на снижение прочности конструкции и неприемлемость использования метода коррозионного тока для оценки снижения прочности. Сравнение скорости разрушения железобетонных конструкций в терминах прочности и жесткости показано на рис. 4.
Скорости снижения прочности и жесткости резко различны: снижение жесткости более значительно, чем прочности. Например, когда жесткость снижается до 60% от начального значения, прочность снижается только на 10%. Причина состоит в том, что жесткость (или прогиб) является мерой механических свойств относительно геометрии конструкции и ее поперечных сечений в большей степени, чем прочность. Другими доминирующими факторами, которые тесно связаны с коррозией, являются трещинообразование в бетоне и потеря сцепления. Все эти эффекты становятся особенно заметными при активном развитии коррозии. Как следствие сильно увеличивается прогиб. Как известно, растянутая зона не включается в расчет прочности нормального сечения железобетонных изгибаемых элементов. Значительное снижение жесткости конструкции свидетельствует о сильном повреждении железобетонных конструкций, тогда как по расчету они обладают достаточной конструкционной прочностью. Последнее имеет место, в частности, еще и потому, что коэффициенты надежности при проектировании прочности обычно выше аналогичных для пригодности к эксплуатации. Поскольку расходы на содержание железобетонных конструкций обычно высоки (в частности, для усиления), поэтому важно для практической деятельности дифференцировать мероприятия по эксплуатации для разных уровней деструкции. В этом смысле рис. 4 может являться руководством для инженеров и эксплуатационников.
Вероятностная модель разрушения конструкции
Поскольку разрушение конструкции имеет вероятностный характер, целесообразно моделировать разрушение конструкции как стохастический процесс, оцениваемый количественно функцией деструкции. Для железобетонных изгибаемых элементов функция разрушения может моделироваться посредством функции, mj(t), и функцией коэффициента вариации Vj (t)
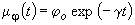
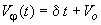
где: jо- начальная функция разрушения (t=0), которая согласуется с определением функции разрушения по формулам (3) и (22), где g - коэффициент, представляющий скорость разрушения конструкции. Это позволяет учитывать влияние таких факторов, как развитие коррозии, структура бетона и особенности конструкции. В формуле (23в) Vо - начальная вариация конструкционных свойств бетона /27/, - коэффициент, представляющий увеличение неопределенности в течение процесса разрушения.
Для применения модели разрушения по формуле (23) на практике может быть использована математическая регрессия для оценки изменения экспериментальных данных. Регрессионный анализ результатов изменения прочности железобетонных изгибаемых элементов представлен в формулах (24а) и (24в):
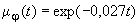
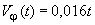
Выражения для средних значений и коэффициента вариации функции снижения жесткости были получены, основываясь на регрессивном анализе результатов испытаний. Функция снижения жесткости может быть выражена следующим образом:

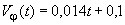
Прогноз долговечности железобетонных конструкций, подверженных коррозии
Используя модели разрушения конструкции, возможно прогнозировать снижение эксплуатационной пригодности и надежности для железобетонных конструкций, подверженных коррозии. Это два ключевых жизненных цикла железобетонных конструкций, критерии которых определяются по формуле (4). В действительности различные принятые критерии дадут в результате различное время эксплуатационной пригодности и безопасности конструкций. Долговременный прогиб может быть в 3-4 раза выше начального прогиба железобетонных изгибаемых элементов с учетом ползучести, усадки, трещинообразования, расслоения, потери сцепления арматуры с бетоном и т.д. Это может соответствовать предельно допускаемому прогибу при разрушении 0,3. Уровень надежности может быть принят равным 90%. Исходя из этого, время до достижения конструкцией состояния непригодности к эксплуатации TSможет быть рассчитано из формулы (4):

Считается /5/, что приемлемым является уровень разрушения 25% в терминах уменьшения поперечного сечения арматурных стержней в железобетонных конструкциях, подверженных коррозии. Этот критерий основан на экспериментальных данных Европейского комитета по бетону. Amex /30/ рассчитывает срок службы подверженных коррозии железобетонных конструкций, используя более упрощенный 30-процентный предел снижения площади стержня как критерий разрушения. Поскольку уменьшение площади стержней коррелируется с прочностью, уменьшение коэффициента в 1,3 раза, как показано на рис. 3, может быть приемлемым, если взять допускаемый предел для снижения прочности 0,6, определенный по формуле (3). Опять-таки, используя доверительный уровень 90%, время до разрушения конструкции может быть рассчитано из формулы (4)
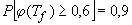
Заключение
Развиты модели разрушения конструкции, используемые в оценке качества в течение всего срока эксплуатации железобетонных конструкций, подверженных коррозии. Модели основаны на результатах, полученных из обширного эксперимента по развитию коррозии в бетоне и ее воздействию на снижение прочности и жесткости конструкции. Критерий оценки установлен для определения качества конструкции в терминах предельных состояний по прочности и пригодности к эксплуатации. Было обосновано, что железобетонные изгибаемые элементы разрушаются с различной скоростью по прочности и по жесткости, причем жесткость снижается быстрее, чем прочность. Используя модели разрушения конструкций, были определены жизненные циклы подвергнутых коррозии конструкций, их надежность и долговечность. Было обосновано, что инициирование коррозии меньше 15% срока службы, после чего железобетонные изгибаемые элементы разрушаются до непригодности к эксплуатации. Поскольку коррозия арматуры приводит к разрушению конструкции, для развития рациональных моделей требуется больше исследований в развитии коррозии и, в частности, экспериментальных исследований.
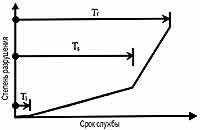
Рис. 1. Схематическая модель жизненных циклов, подверженных коррозии железобетонных конструкций
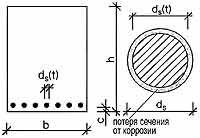
Рис. 2. Поперечное сечение балки (слева) с корродирующей рабочей арматурой (справа)
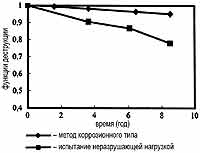
Рис. 3. Сравнение снижения прочности, определенной разными методами
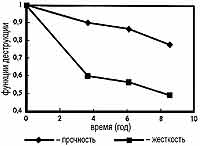
Рис. 4. Сравнение сопротивления разрушению по прочности и по жесткости
Литература
1. Tonini, D.E., and Dean, S.W. (1976). «Chloride corrosion of steel in concrete». ASTM STP 629, Philadelphia.
2. ACI Committee 222 (ACI C222). (1985). «Corrosion of metals in concrete». ACI J., 82(1), 3-32.
3. Schiessl, P.(1988). «Corrosion of steel in concrete». Rep. of the TC 60 - CSC RILEM, Chapman and Hall. London.
4. Berke, N.S., Chaker, V., and Whiting., eds. (1990). «Corrosion rates of steel in concrete». ASTM STP 1065, Philadelphia.
5. Andrade, C., Alonco, M.C., Feliu, S., and Gonzalez, J.A. (1996). «Advances in the on-site electrochemical measurement of reinforcement corrosion and their use for predicting residual life». Proc. of 13th Intern. Conf. on Corrosion, Melbourne, Australia, 3.1-3.7.
6. Andrade, C., Martinez, I. (2003). On site techniques for corrosion rate monitoring in real structures // Durability Design and Fracture Mechanics of concrete structures: Proc. Int. Conf. «Construction and Architecture». Edit. Khroustaliev, Leonovich. Minsk, 2003, p. 17-26. 7. Bamforth, P.B. (1999). «The derivation of input data for modeling chloride ingress from eight-year UK coastal exposure trials». Mag. Concrete Res., 51(2), 89-96.
8. De Scutter, G. (1999), «Quantification of the influence of cracks in concrete structures on carbonation and chloride penetration». Mag. Concrete Res., 51 (6), 427-435.
9. Otsuki, N., Miyazato, S., Diola, N.B., and Suzuki, H. (2000). «Influences of bending crack and water-cement ratio on chloride-induced corrosion of main reinforcing bars and stirrups». ACI Mater. J., 97(4), 454-465.
10. Roberts, M.B., Atkins, C., Hogg, V., and Middleton, C. (2000). «A proposed empirical corrosion model for reinforced concrete». Struct. Bldg. I.C.E., 140(1), 1-11.
11. Francois, R., and Castel, A. (2001). «Discussion on influences of bending crack and water-cement radio on chloride-induced corrosion of main reinforcing bars and stirrups» ACI Mater. J., 98(3), 276-278.
12. Frangopol, D.M., Lin, K.Y., and Estes, A. (1997). «Reliability of reinforced concrete girders under corrosion attack». J. Stauct. Eng. 123(3). 286-297.
13. Leeming, M.B. (1998). «Durability of concrete in and near the sea». Concrete in coastal structures, R.T.L. Allen, ed., Thomas Telford, London, 73-98.
14. Li, C.Q. (2003). «Life-cycle modeling of Corrosion-Affected concrete structures: Propagation». J. Struct. Eng. ASCE, 129(6), 753-761. 15. Леонович С.Н. Алгоритм расчета долговечности железобетонных конструкций при карбонизации // Перспективы развития новых технологий в строительстве и подготовке инженерных кадров в Республики Беларусь. Материалы VI Международного научно-технического семинара. - Мн.: УП «Технопринт», 2000, С. 220-225.
16. Леонович С.Н. Теоретические основы расчета, долговечности железобетона при карбонизации // Перспективы развития новых технологий в строительстве и подготовке инженерных кадров в Республике Беларусь. Материалы VI Международного научно-технического семинара. - Мн.: УП «Технопринт», 2000, С. 225-237.
17. Леонович С.Н. Алгоритм расчета долговечности железобетонных конструкций при хлоридной агрессии // Перспективы развития новых технологий в строительстве и подготовке кадров Республики Беларусь. Сборник трудов VII Международного научно-методического семинара. - Брест, БГТУ, 2001, С. 432-435.
18. Леонович С.Н. Вероятностная оценка коррозии арматуры в существующих железобетонных конструкциях при хлоридной агрессии // Перспективы развития новых технологий в строительстве и подготовке кадров Республики Беларусь. Сборник трудов VII Международного научно-методического семинара. - Брест, БГТУ, 2001, С. 435-440.
19. Tuutti, K. (1982). «Corrosion of steel in concrete». Swedish Cement and Concrete Research Institute, Stockholm, Sweden, 17-21.
20. Almusallam, A.A., Al-Gahtani, A.S. Aziz, F.R., Dakhil, F.H. and Rasheeduzzafar. (1996) «Effect of reinforcement corrosion on flexural behavior of concrete slabs». J. Mater. Civ. Eng., 8(3), 126-127.
21. Cleven, M. Li, C.Q., and Isaac, F. (1999) «Bond loss due to reinforcing steel corrosion in concrete». Proc., 14th Int. Corrosion Conf. Sept. 27 - Oct. 1, Cape Town, 34.1-34.10.
22. American Concrete Institute (ACE). (1989). «Building code requirements for reinforced concrete». ACI 318, Farmington Hills, Mich. 23. СНБ 5.03.01-02 «Бетонные и железобетонные конструкции».
24. Vi?an, J. Kote?, P. (2003). Reliability of concrete structure member under corrosion attack // Durability Design and Fracture Mechanics of concrete structures: Proc. Int. Conf. «Construction and Architecture». Edit. Khroustaliev, Leonovich. Minsk, 2003, p. 38-47.
25. Jones, D.A. (1992). «Principles of and prevention of corrosion». Macmillan, New York.
26. Broomfield, J. (1997). «Corrosion of steel in concrete. Understanding, investigation ( repair». E ( FN Spon, London.
27. Mirza, S.A., Hatzinikolas, M., and MacGregor, J.G. (1979). «Statistical description of strength of concrete». J. Struct. Div. ASCE, 105(6), 1021-1037.
28. Papoulis, A. (1965). «Probability, random variables, and stochastic processes». Mc Graw-Hill, New York.
29. ASTM. (1991). «Standard test method for half-cell potentials of uncoated reinforcing steel in concrete». C - 876, Philadelphia, 425-430. 30. Amey, S.L., Johnson, D.A., Miltenberger, M.A., and Farzam, H. (1998). «Predicting the service life of concrete marine structures: An environment methodology». ACI Mater. J., 95(2), 205-214.
31. Thoft-Christensen, P. (1992). «Reliability Based Expert System for Bridge Maintanance». Tekho Vision Conference, Denmark, 1992. 32. Frey, R. (1993). «Untersuchung der zwanzigiдhring Carbonatisierung von Betonen». Beton 43, 1993, Helt 3, p. 116-120.
33. Васильев А.И. Оценка коррозионного износа рабочей арматуры в балках пролетных строений автодорожных мостов // Бетон и железобетон. - 2000. - №2. - С. 20-23.
34. Andrade С., Alonso С., Rodriguez J., Garsia М. Cover cracking and amount of rebar corrosion: Importance of the current applied accelerated tests. Concrete Repair, Rehabilitation and Protection. Edited by R.К. Dhir and М. R. Jones, E & FN Spon, London,1996, р. 263-273.
35. Томашов Н.Д. Теория коррозии и защиты металлов. - М., 1962.
Сергей ЛЕОНОВИЧ, ДОКТОР ТЕХН. НАУК, ПРОФЕССОР (БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИчЕСКИЙ УНИВЕРСИТЕТ)
Строительство и недвижимость. Статья была опубликована в номере 08 за 2005 год в рубрике материалы и технологии


