К расчету сооружений на ветровую нагрузку
Известно, что основной нагрузкой для высотных сооружений является ветровая. Однако в современных пакетах автоматизированного расчета крайне скудно освещена теоретическая база расчета сооружений на ветровую нагрузку, что затрудняет их использование проектировщиками. Авторы настоящей статьи, в которой кратко излагаются некоторые теоретические основы расчета сооружений на ветровую нагрузку по нормам /1/ и приведены два примера, выражают надежду, что она в некоторой степени поможет инженерам-проектировщикам более эффективно использовать пакет “ЛИРА” и другие программные средства.
Ветровое нормальное давление на препятствие определяется по формуле /2/:

где
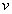

Скорость и направление ветра в данной точке считаются непостоянными, зависящими от времени. На рис. 1 по данным /2/ изображен график зависимости скорости ветра от времени, из которого видно, что скорость ветра осциллирует или пульсирует около среднего значения

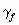
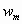

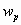

где
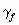

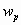
Величина
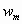

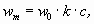
где
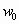
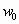


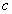
На физическом смысле коэффициентасследует остановиться подробнее. Каждое здание с точки зрения аэродинамики является плохообтекаемым препятствием /4/. На рис. 2а по данным /2/ изображена картина обтекания здания потоком воздуха, где ясно видны зоны вихреобразования, зона турбулентности, а на рис. 2б — распределение ветрового давления по наружным поверхностям этого здания. Отметим, что в зависимости от скорости ветра, плотности воздуха, формы здания и шероховатости его наружных стен, наличия соседних сооружений, холмов и т.д. картина распределения давления может быть иной. При определении проекций ветровой нагрузки на различные направления в приложении 4 /1/ приводятся величиныcx,cy,ce,cfи аэродинамического коэффициента внутреннего давленияci.
Т.к. вероятностные характеристики ветрового давления с течением времени не меняются, то пульсация скорости ветра в точке турбулентного потока рассматривается как стационарный случайный процесс. Устанавливая корреляционные функции турбулентного ветрового потока на основании обработки экспериментальных данных, находят спектральную плотность и среднее квадратичное значение реакции для сооружения. Это позволяет определить средние квадратичные значения динамических перемещений сооружения и коэффициент динамичности. Потом строится график нормативного динамического коэффициента с учетом материала, из которого выполнено сооружение.
Нормативное значение пульсационной составляющей ветровой нагрузкиwpопределяется поwmв зависимости от динамических характеристик (собственных частот, степеней свободы и коэффициента внутреннего трения) сооружения, на которое действует ветровая нагрузка. Ветровое давление является существенно динамической нагрузкой, так как при ее действии в общем случае может меняться величина нагрузки, место ее приложения и направление. Вследствие упругих свойств сооружения при действии порывов ветра оно колеблется. При колебаниях в элементах сооружения возникают силы инерции, которые влияют на напряженно-деформированное состояние сооружения. В зависимости от соотношения между частотами собственных колебаний сооружения и частотой пульсации ветра, частотой срыва вихрей воздуха с сооружения в нем могут возникнуть случаи, близкие к резонансу. Это приведет к значительному увеличению усилий, напряжений и перемещений в элементах сооружения. Поэтому в нормах /1/ приводятся предельные значенияflчастот собственных колебаний сооружения в зависимости от ветрового района и материала сооружения, при которых допускается не учитывать пульсационную составляющую ветровой нагрузки. Если жеflнаходится в нижней части спектра собственных частот сооружения, то нормы рекомендуют рассматривать три случая.
Случай А:
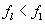
Тогда

где
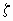

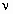
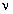
Случай Б:
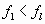
Относится к системам с одной степенью свободы (водонапорные башни, ветроэнергетические установки, ретрансляторы и другие мачтовые сооружения).

где: x


Случай В:если


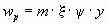
где:

y— условное горизонтальное перемещение на уровнеzпо первой форме собственных колебаний;
y — коэффициент, определяемый посредством разделения сооружения наrучастков, в пределах которых ветровая нагрузка принимается постоянной, по формуле

гдеMk— массаk-го участка сооружения;
yk— условное горизонтальное перемещение по первой форме собственных колебаний на уровне расположения массы
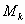
wpk— равнодействующая пульсационной составляющей ветровой нагрузки наk-ом участке сооружения. Определяется по формуле (4).
Случай Г:
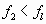
Необходимо производить расчет с учетом первыхsформ собственных колебаний, где число

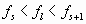
Из вышеизложенного ясно, как сложен расчет на действие ветровой нагрузки. Он состоит из двух этапов. На первом инженер определяет частоты и формы собственных колебаний сооружения, на втором — производит расчет в зависимости от положенияflв спектре собственных колебаний сооружения.
Все эти случаи расчета запрограммированы в пакете “ЛИРА-Windows”. В пакете пульсационная составляющая ветровой нагрузки раскладывается в ряд по собственным формам колебаний конструкции, и расчет ведется для каждого члена ряда отдельно. При этом считается, что сооружение реагирует каждой формой своих собственных колебаний на ветровую нагрузку. Определяются дляi-го слагаемого разложения в ряд ветровой нагрузки силы инерцииZiкаждой колеблющейся массы. По ним определяются усилияMi,Qi,Niи перемещения. Суммарное усилие на стадии вычисления расчетных сочетаний определяется по формуле:

гдеNk— усилие в сечении от статической составляющей ветровой нагрузки;Ni— то же отi-го слагаемого пульсационной составляющей ветровой нагрузки.
Примеры расчета
Пример 1.Расчет дымовой трубы на пульсацию (пример передан инженером С.А. Черновой, институт “Белпромпроект”, Минск).
Исходные данные:
— труба по ГОСТ 1074-76 сdн= 630 мм иdв= 610 мм;
— высота трубы — 20 м;
— ветровой район — I, тип местности — B;
— предельное значение частоты собственных колебанийfl= 2,9 Гц (табл. 8, /1/).
Перед расчетом трубы на ветровую пульсацию находим частоты собственных колебаний трубыf1иf2с двумя массами и формы собственных колебаний. Воспользовавшись программным пакетом “ЛИРА”, на основании модального анализа получим:
а) частоты собственных колебаний:f1= 1,6672 Гц ;f2= 13,8748 Гц;
б) горизонтальные перемещения масс в соответствии с формами собственных колебаний (рис. 3):
— форма I —Y1I= 100 мм;Y2I= 667 мм;
— форма II —Y1II= 674 мм;Y2II= –101 мм.
Аэродинамический коэффициентсопределяем по Приложению 4 — /1/, номер схемы 14:
с = к× сxh= 0,91× 0,59 = 0,54,
гдекопределяется по таблице 1 схемы 13 в зависимости от параметра le= 2× 20/0,63 = 63,4921;
сxhопределяется по графику схемы 14 в зависимости от числа Рейнольдса (Re= 9,17 × 105,схема 12а) ветрового потока и отношения Δ/d= 0,0016.
Нормативное значение средней составляющей ветровой нагрузки на высотах 5, 10 и 15 м по формуле 6 /1/ будет соответственно 6,21, 8,07 и 10,56 кгс/м2. Т.к. в нашем случае
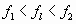
wp=m×x× y× g.
m1=m2= 1539/(10× 0,63) = 242,698 кг/м2;

по чертежу 2 /1/ коэффициент динамичности x = 1,51.
Т.к. участков с различной величинойwpтри, а масс — две, то для первой массы принимаем среднее значениеwp(приz= 5 м иz= 10 м). Итак, по таблицам 7, 9 и 10 /1/ для первой массы z = 1,14, n = 0,88, для второй массы — z= 0,92, n = 0,88.
Равнодействующая пульсационной составляющей ветровой нагрузки для участков с массамиm1иm2:
wp1=(62,1 + 88,7)/2× 10× 0,63× 1,14× 0,88 = 451,259 Н;
wp2=105,6× 10× 0,63× 0,92× 0,88 = 538,611 Н.
По формуле 11 /1/ коэффициент y при горизонтальных перемещениях на уровнеzпо первой форме собственных колебанийy1I= 100 иy2I= 667:
y = (100× 451,259 + 667× 538,611) / (1002×1529 + 6672×1529) = 0,0005814.
Поэтому на высоте расположения первой массыz= 5 м:
wp= 242,698× 1,51× 0,0005814× 100 = 21,307 Па.
То же на высоте расположения второй массыz= 15 м:
wp= 242,698× 1,51× 0,0005814× 667 = 142,116 Па.
Согласно п. 6.8 /1/ для сооружений цилиндрической формы при
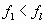
vкр1=d/ (T1×Sh) = 0,63 / (0,5998× 0,2) = 5,25 м/сек >vкр, min= 0,64

где:T1иT2— периоды собственных колебаний;
Sh= 0,2 — число Струхаля для поперечного сечения в виде круга.
Как отмечается в /2/, для сооружений консольного типа допускается учитывать только первую форму собственных колебаний. Амплитуда динамической силы на уровне расположения первой массы при колебаниях по первой форме по формуле 30 /5/:
F1(5) =F01× a 1(5) = 2,661× 100/667 = 0,4 Н/м,
где: a1(5) — относительная ордината первой формы собственных колебаний на высотеz= 5 м;
F01=cy×qкр,1×d= 0,25× 0,613× 5,252×0,63 = 2,661 Н/м — амплитуда интенсивности динамической силы на уровне свободного конца трубы.
Амплитуда динамической силы на уровне расположения второй массы при колебаниях по первой форме:
F1(15) =F01× a 1(15) = 2,661× 667/667 = 2,661 Н/м;
Находим момент в защемлении и прогиб верха трубы от статического действияF1(5) иF1(15):
М= 0,4× 10× 5 + 2,661× 10× 15 = 419,15 Нм.
f= 5,288 мм (получено из расчета по программе “ЛИРА” от статического действия ветровой нагрузки.
По формуле 31 /5/ резонансный момент и перемещение:
Мрез= p /d ×Мс= 3,14/0,15× 419,15 = 8778,66 Нм;
fрез= p /d ×fc= 3,14/0,15× 5,288 = 110,752 мм.
Далее определяются расчетные величины с учетом коэффициента надежности по ветровой нагрузке gf= 1,4.
Пример 2.Расчет связевого каркаса жилого многоэтажного дома в районе проспекта Пушкина и улиц Притыцкого и Д. Сердича в г. Минске (пример передан инженером В.И. Ореховым, институт “Минскгражданпроект”).
Высота здания от верха фундаментной плиты до оси самого верхнего ригеля — 54,375 м. Размеры здания в плане приведены на рис. 4.
Машинный расчет каркаса выполнялся на 16 загружений:
1, 2 — постоянная нагрузка; 3 — временная длительно действующая; 4 — кратковременная снеговая; 5-8 — ветер в направлении осейOXиOY; 9-10 — ветер по диагонали здания; 11-16 — распределение весов масс для расчета на пульсационное воздействие ветра.
При определении ветровой нагрузки на горизонтальные элементы каркаса здания вначале рассчитывалась вертикальная неразрезная балка с числом пролетов, равным числу этажей, на действие горизонтального ветрового давления. Усилия в опорах неразрезной балки на уровне каждого междуэтажного перекрытия давали погонную ветровую нагрузку на крайние горизонтальные ригеля каркаса здания. При определении ветрового давления, направленного нормально диагоналям здания, менялся аэродинамический коэффициентсв формуле (3), и, следовательно, величинаwm.
Нормы /5/ рекомендуют при определении частот и форм собственных колебаний рассматриваемого здания принимать вертикальный защемленный стержень с равномерно расположенными по высоте массами. Однако рассматриваемое здание с металлическими связями обладало большой горизонтальной податливостью, и следовало ожидать, что первыми формами колебаний будут изгибно-крутильные. Чтобы их не потерять, распределение массы здания на сосредоточенные производилось по следующему принципу. По разнице продольных сил от постоянной нагрузки в колоннах смежных этажей определялась величина массы междуэтажного перекрытия. Эта масса распределялась на 4 сосредоточенные в углах прямоугольного участка перекрытия. Так как здание имело почти симметричную форму в плане, то массы также распределялись симметрично на пересечениях осей 3-В, 3-Е, 5-В, 5-Е (рис. 4). Считалось, что каждая масса обладала тремя степенями свободы. На фундаментную плиту передавалась масса лифта. (В некоторых пакетах распределение весов масс автоматизировано.)
Вначале расчетом были определены частоты и формы собственных колебаний здания (модальный анализ). Распределение частот собственных колебаний здания дано в таблице.
№ п/п | Собственные значения | Частоты | Периоды | |
1/с | Гц | с | ||
1 | 1,12391 | 0,8898 | 0,1417 | 7,0581 |
2 | 0,93918 | 1,0648 | 0,1695 | 5,8980 |
3 | 0,61304 | 1,6312 | 0,2597 | 3,8499 |
4 | 0,28435 | 3,5168 | 0,5600 | 1,7857 |
5 | 0,22767 | 4,3923 | 0,6994 | 1,4297 |
6 | 0,18950 | 5,2771 | 0,8403 | 1,1900 |
7 | 0,14412 | 6,9385 | 1,1049 | 0,9051 |
8 | 0,12513 | 7,9915 | 1,2725 | 0,7858 |
9 | 0,11271 | 8,8720 | 1,4127 | 0,7078 |
10 | 0,10800 | 9,2593 | 1,4774 | 0,6782 |
11 | 0,10445 | 9,5740 | 1,5245 | 0,6559 |
12 | 0,09980 | 10,0196 | 1,5995 | 0,6267 |
13 | 0,09883 | 10,1181 | 1,6112 | 0,6206 |
14 | 0,09825 | 10,1783 | 1,6208 | 0,6170 |
15 | 0,09301 | 10,7511 | 1,7120 | 0,5841 |
16 | 0,08701 | 11,4927 | 1,8300 | 0,5464 |
17 | 0,07675 | 13,0290 | 2,0747 | 0,4820 |
18 | 0,07584 | 13,1855 | 2,0996 | 0,4762 |
19 | 0,07369 | 13,5700 | 2,1608 | 0,4627 |
20 | 0,07203 | 13,8837 | 2,2108 | 0,4523 |
21 | 0,06880 | 14,5361 | 2,3145 | 0,4320 |
22 | 0,06424 | 15,5658 | 2,4786 | 0,4034 |
23 | 0,06355 | 15,7348 | 2,5055 | 0,3991 |
24 | 0,06188 | 16,1605 | 2,5733 | 0,3886 |
25 | 0,05975 | 16,7371 | 2,6651 | 0,3752 |
26 | 0,05529 | 18,0861 | 2,8799 | 0,3472 |
27 | 0,05473 | 18,2705 | 2,9093 | 0,3437 |
Из анализа данных таблицы следует, что при заполнении документа 15 исходных данных для машинного расчета по ПК “ЛИРА-Windows” необходимо учитывать 26 форм собственных колебаний здания (случай Г).
На рис. 5 показана в плане первая форма собственных колебаний каркаса рассчитываемого здания, из которой видно, что она является именно изгибно-крутильной, которая была бы не учтена при замене каркаса консольной вертикальной балкой для определения частот собственных колебаний.
Расчеты показали, что наиболее опасным оказалось диагональное воздействие ветра, что потребовало увеличения жесткостных параметров вертикальных связей в каркасе здания. Это, в свою очередь, потребовало повторного определения весов масс и выполнения модального анализа.
В процессе работы над статьей инженер С.Д. Минчук (ОАО “Белпроект”) указал авторам на необходимость учета временной длительно действующей нагрузки при определении весов масс (пример 2). Однако в предлагаемом расчете доля временной длительно действующей нагрузки составляла всего 14% от постоянной, что при расчете привело бы к уменьшению первых частот собственных колебаний приблизительно на 7%. В то же время нормы прямо не указывают, с каким коэффициентом сочетаний необходимо брать эту долю внешней нагрузки при определении весов масс. Поэтому, в принципе соглашаясь с замечанием С.Д. Минчука о необходимости двойного динамического расчета здания на стадии строительства до пуска отопления и в стадии эксплуатации со всеми сопутствующими временными нагрузками, авторы сочли возможным пренебречь влиянием временной длительно действующей нагрузки при расчете здания на пульсацию.
Авторы отдают себе отчет в том, что материал статьи далеко не в полной мере охватывает все случаи действия ветровой нагрузки на сооружение. Это невозможно сделать в силу многообразия встречающихся случаев расчета и учета такого сложного вида нагружения, как ветровое. Однако если содержание статьи поможет инженеру-проектировщику в его работе, то цель авторов будет достигнута.

Рис. 1. Зависимость скорости ветра от времени
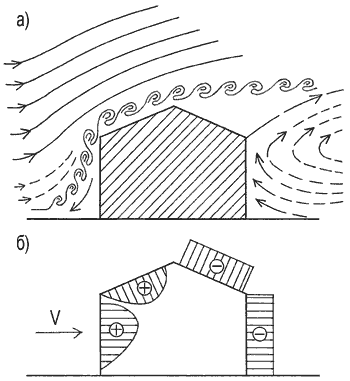
Рис. 2. Обтекание сооружения ветровым потоком
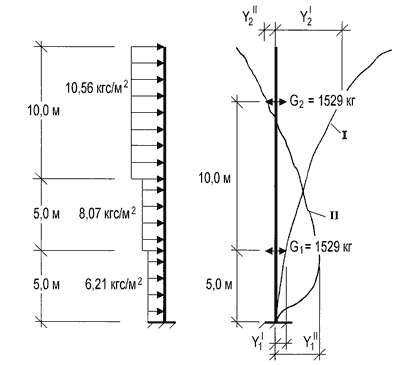
Рис. 3. Расчетная схема дымовой трубы с распределением по высоте масс и нормативной средней составляющей ветрового давления

Рис. 4. План фундаментной плиты и разбивка осей здания

Рис. 5. Вид в плане элементов металлического каркаса при первой изгибно-крутильной форме колебаний здания.
Литература
1. СНиП 2.01.07-85*. Нагрузки и воздействия. М., 1986.
2. Савицкий Г.А. Ветровая нагрузка на сооружения. М.: Стройиздат, 1972.
3. Беспрозванная И.М., Соколов А.Г., Фомин Г.М. Воздействие ветра на высокие сплошностенные сооружения. М.: Стройиздат, 1976.
4. Симиу Э., Сканлан Р. Воздействие ветра на здания и сооружения. М.: Стройиздат, 1978.
5. Руководство по расчету зданий и сооружений на воздействие ветра. М.: Стройиздат, 1978.
Сергей БОСАКОВ, доктор техн. наук, профессор БНТУ,
Олег КАЛОША, главн. специалист института “Минскпроект”
Строительство и недвижимость. Статья была опубликована в номере 48 за 2003 год в рубрике наука


