MathCAD — это просто! Часть 31. Собственно статистика
В прошлый раз, если вы помните (а я надеюсь, вы действительно помните), мы с вами занимались тем, что импортировали данные в MathCAD извне. Безусловно, уметь это делать просто необходимо. Я уверен в том, что большая часть проектов, которые вы делаете в MathCAD'е, так или иначе связана с обработкой каких-то внешних данных: построением моделей, расчетом параметров систем — и т.д., и т.п. Однако практически обо всем, что связано с построением математических моделей, мы уже поговорили. Дело только за математической статистикой — к ней, не откладывая в долгий ящик, прямо сейчас мы с вами и приступим.
Вы, конечно, можете спросить, а есть ли вообще смысл заниматься статистическими вычислениями именно в MathCAD'е? Ведь есть специальные пакеты (один, кстати, так и называется — Statistica), которые наверняка специально заточены под различные статистические задачи. Возможно, было бы правильнее и разумнее воспользоваться именно этими узкоспециализированными пакетами, а не "математическим монстром" в лице MathCAD'а? Что ж, вопрос закономерный, и, я бы даже сказал, действительно хороший. Однако эти пакеты, во-первых, стоят не сказать чтобы прямо уж очень дешево (кто не верит — может погуглить, сколько именно придется выложить за тот же пакет Statistica); во-вторых, их также еще нужно будет изучать, поскольку любая программа, обладающая большим спектром возможностей — это довольно-таки сложный инструмент, который не принесет никакой пользы в неумелых руках; ну, а в-третьих, если вы планируете заниматься не только статистическими расчетами в рамках решаемой вами задачи, а, скажем, также решением дифференциальных уравнений, то применение специализированного статистического программного обеспечения для сравнительно несложных расчетов будет сродни стрельбе из пушек по воробьям. В связи со всем этим, как видите, как бы так вот даже и само собой получается, что использовать MathCAD для математической статистики — очень даже рентабельно и разумно, если, конечно же, умеешь пользоваться MathCAD'ом и худо- бедно знаешь эту самую математическую статистику.
Комбинаторные вычисления
Начнем разговор о математической статистике издалека (хотя это "далеко" сравнительное), а именно с комбинаторных вычислений, или попросту комбинаторики. Что есть комбинаторика? Это, если верить Википедии, "раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка)". Можно, конечно, Википедии и не верить, но смысл и содержание комбинаторики как науки от этого нашего с вами неверия ничуть не изменится. Потому что комбинаторика — это действительно раздел математики, преимущественно считающий способы перестановки элементов упорядоченных множеств. Каким образом комбинаторика относится к математической статистике? Дело в том, что статистика базируется на теории вероятностей — очень удобной и во многом гениальной математической теории, позволяющей осуществлять численный анализ множества явлений, не вдаваясь в их глубинную природу. С точки зрения теории вероятностей комбинаторика — отличный инструмент решения некоторых ее задач, достаточно простых, но местами просто необходимых для построения базиса методов решения задач более сложных. Да и потом, если задача и простая, это ведь не отменяет необходимости искать ее решение. Так что комбинаторные вычисления — очень даже реальная задача, с которой можно столкнуться в любой момент. Два кита комбинаторики — это понятия размещения и сочетания. Фактически это довольно близкие и во многом даже, можно сказать, аналогичные друг другу понятия, с той лишь разницей, что для размещения учитывается порядок элементов, а для сочетания — нет. Таким образом, число размещений — это общее количество различных наборов при выборе k элементов из n без возвращения и с учетом порядка. Число сочетаний — общее количество различных наборов при выборе k элементов из n без возвращения и без учета порядка. Вычислить количество размещений и сочетаний можно следующим образом по довольно-таки простым формулам:
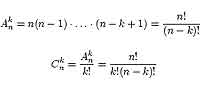 Как видите, комбинаторные формулы, которые будут применяться в вычислениях, действительно просты, и не составит никакого труда записать их в том же MathCAD'е. Но в этом, в общем-то, нет никакой насущной необходимости по той простой причине, что в MathCAD'е уже есть встроенные функции, позволяющие и безо всякого написания факториалов вручную вычислить число размещений и число сочетаний. Называются они, соответственно, по английским названиям терминов "размещение" и "сочетание" — permut (от permutation) и combin (от combination). У обеих функций всего два параметра. Каких именно? Об этом совсем не сложно догадаться, если посмотреть на формулы для числа размещений и числа сочетаний — конечно же, эти параметры — это те самые n и k, которые соответствуют общему числу элементов в множестве и числу выбираемых нами элементов в этом же самом множестве. Обратите, пожалуйста, внимание на порядок следования параметров: первым идет именно параметр, задающий n, а вторым — уже тот, который задает число k. Поскольку комбинаторные задачи, которые предполагает использование тех функций, о которых я только что рассказал, так же просты, как и сами эти функции, то я приводить их примеров не буду. Продемонстрирую только то, что функции действительно считают то, что было обещано. Вы можете сами повторить вычисления с использованием приведенных выше формул и с заданными параметрами. На скриншоте вы также можете увидеть тот факт, что при попытке посчитать число размещений и число сочетаний при k > n среда MathCAD выдает нам ошибку.
Как видите, комбинаторные формулы, которые будут применяться в вычислениях, действительно просты, и не составит никакого труда записать их в том же MathCAD'е. Но в этом, в общем-то, нет никакой насущной необходимости по той простой причине, что в MathCAD'е уже есть встроенные функции, позволяющие и безо всякого написания факториалов вручную вычислить число размещений и число сочетаний. Называются они, соответственно, по английским названиям терминов "размещение" и "сочетание" — permut (от permutation) и combin (от combination). У обеих функций всего два параметра. Каких именно? Об этом совсем не сложно догадаться, если посмотреть на формулы для числа размещений и числа сочетаний — конечно же, эти параметры — это те самые n и k, которые соответствуют общему числу элементов в множестве и числу выбираемых нами элементов в этом же самом множестве. Обратите, пожалуйста, внимание на порядок следования параметров: первым идет именно параметр, задающий n, а вторым — уже тот, который задает число k. Поскольку комбинаторные задачи, которые предполагает использование тех функций, о которых я только что рассказал, так же просты, как и сами эти функции, то я приводить их примеров не буду. Продемонстрирую только то, что функции действительно считают то, что было обещано. Вы можете сами повторить вычисления с использованием приведенных выше формул и с заданными параметрами. На скриншоте вы также можете увидеть тот факт, что при попытке посчитать число размещений и число сочетаний при k > n среда MathCAD выдает нам ошибку.
Распределения
К сожалению (а может быть, и наоборот), одной только комбинаторикой отделаться не удастся. Поэтому перейдем к более существенным с практической точки зрения вещам — к такому основополагающему для статистики понятию, как распределение. Для того, чтобы вспомнить, что такое распределение, обратимся, опять-таки, все к той же Википедии: "распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия". Конечно, Википедия, редактируемая всеми, кому не лень, довольно часто дает, скажем так, не слишком достоверную информацию. Однако здесь, как и в случае с комбинаторикой, все совершенно верно. Распределения делятся на два больших класса: дискретные и непрерывные. Дискретные распределения описывают свойства дискретных случайных величин; непрерывные, соответственно, непрерывных. Разных распределений, как дискретных, так и непрерывных, существует великое множество, однако практическое применение нашли сравнительно немногие из них. Среди дискретных наиболее часто встречаются в практических задачах распределения Бернулли, биномиальное, геометрическое, гипергеометрическое, логарифмическое, отрицательное биномиальное, Пуассона и равномерное. Из непрерывных — Колмогорова, Коши, Лапласа, Гаусса (оно также называется нормальным), равномерное, Стьюдента, Фишера, хи-квадрат и экспоненциальное. Конечно, мы с вами не будем сейчас рассматривать законы, описывающие каждое из этих распределений — это уже отдельная тема. Ознакомиться с ними, если возникнет такая необходимость, можно по любому учебнику и справочнику по математической статистике. Самый главный параметр, описывающий распределение — это плотность вероятности. С ее помощью можно вычислить вероятность нахождения случайной величины в заданном диапазоне. Для дискретной случайной величины вероятность находится с помощью суммирования, а для непрерывной — соответственно, с помощью интегрирования. При этом в последнем случае будет справедлива формула: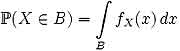
Здесь, конечно же P(x) — это собственно вероятность, а fx(x) — плотность вероятности. Так что, как видите, все довольно просто. В MathCAD есть встроенные функции, которые позволяют вычислить вероятность для разных распределений с заданными параметрами. Поскольку распределений много, и параметры у них у всех разные, мы с вами не будем пытаться догнать всех зайцев, а остановимся только на одном из них — на нормальном, или Гауссовом, распределении. Для моделирования случайных величин, чьи распределения описываются Гауссовой формулой, в MathCAD'е существует специальная функция — dnorm. У нее три параметра. Первый — это переменная x, которую пояснять, я так думаю, не нужно. Второй — это точка по оси x, на которую придется пик распределения (см. соответствующий рисунок). Третий — это дисперсия. Обратимся снова к Википедии: "дисперсия случайной величины — мера разброса данной случайной величины, т.е. ее отклонения от математического ожидания". Для нормального распределения математическим ожиданием является среднее для всех случайных величин значение. Работая с функцией dnorm, очень просто построить график для нормального распределения, который наверняка большинству из вас знаком еще по вузовскому курсу математики. Как видите, на графике действительно очень легко узнать характерный Гауссов контур, похожий на колокол. Вершина, как и было задано выше функцией dnorm, располагается в точке x = 5.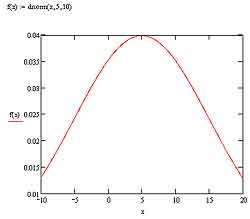
Что ж, пока что, пожалуй, хватит. Думаю, сведений вы пока и так получили достаточно, а комбинаторика и распределения — это действительно интересно, и вы можете самостоятельно поэкспериментировать со всем этим в MathCAD'е.
Выводы
Ну, что ж, по традиции подведем итоги всему тому, что мы уже сказали выше. Итогов, конечно, будет не слишком много, потому что и сказано было не так уж много… Но, тем не менее, без них статья была бы какой-то неполной и незаконченной, да и традиция, как ни крути, есть традиция. Итак, во-первых, как мы с вами, надеюсь, все-таки убедились, использовать MathCAD в статистических расчетах — совсем не такая плохая идея, как кому-то могло бы показаться. Во-вторых, работать с комбинаторными вычислениями в MathCAD'е действительно проще простого, и для этого вам даже не потребуется вручную вводить громоздкие формулы с факториалами. В-третьих, что касается разных распределений, то, хотя мы с вами рассмотрели только нормальное (Гауссово), это не означает, что MathCAD знает только его. Список всех остальных распределений и соответствующих им функций можно найти в справочной системе MathCAD'а. Попробуйте сделать примеры с какими-нибудь другими распределениями, и вы убедитесь в том, что MathCAD отлично умеет с ними работать.
SF, spaceflyer@tut.by
Вы, конечно, можете спросить, а есть ли вообще смысл заниматься статистическими вычислениями именно в MathCAD'е? Ведь есть специальные пакеты (один, кстати, так и называется — Statistica), которые наверняка специально заточены под различные статистические задачи. Возможно, было бы правильнее и разумнее воспользоваться именно этими узкоспециализированными пакетами, а не "математическим монстром" в лице MathCAD'а? Что ж, вопрос закономерный, и, я бы даже сказал, действительно хороший. Однако эти пакеты, во-первых, стоят не сказать чтобы прямо уж очень дешево (кто не верит — может погуглить, сколько именно придется выложить за тот же пакет Statistica); во-вторых, их также еще нужно будет изучать, поскольку любая программа, обладающая большим спектром возможностей — это довольно-таки сложный инструмент, который не принесет никакой пользы в неумелых руках; ну, а в-третьих, если вы планируете заниматься не только статистическими расчетами в рамках решаемой вами задачи, а, скажем, также решением дифференциальных уравнений, то применение специализированного статистического программного обеспечения для сравнительно несложных расчетов будет сродни стрельбе из пушек по воробьям. В связи со всем этим, как видите, как бы так вот даже и само собой получается, что использовать MathCAD для математической статистики — очень даже рентабельно и разумно, если, конечно же, умеешь пользоваться MathCAD'ом и худо- бедно знаешь эту самую математическую статистику.
Комбинаторные вычисления
Начнем разговор о математической статистике издалека (хотя это "далеко" сравнительное), а именно с комбинаторных вычислений, или попросту комбинаторики. Что есть комбинаторика? Это, если верить Википедии, "раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка)". Можно, конечно, Википедии и не верить, но смысл и содержание комбинаторики как науки от этого нашего с вами неверия ничуть не изменится. Потому что комбинаторика — это действительно раздел математики, преимущественно считающий способы перестановки элементов упорядоченных множеств. Каким образом комбинаторика относится к математической статистике? Дело в том, что статистика базируется на теории вероятностей — очень удобной и во многом гениальной математической теории, позволяющей осуществлять численный анализ множества явлений, не вдаваясь в их глубинную природу. С точки зрения теории вероятностей комбинаторика — отличный инструмент решения некоторых ее задач, достаточно простых, но местами просто необходимых для построения базиса методов решения задач более сложных. Да и потом, если задача и простая, это ведь не отменяет необходимости искать ее решение. Так что комбинаторные вычисления — очень даже реальная задача, с которой можно столкнуться в любой момент. Два кита комбинаторики — это понятия размещения и сочетания. Фактически это довольно близкие и во многом даже, можно сказать, аналогичные друг другу понятия, с той лишь разницей, что для размещения учитывается порядок элементов, а для сочетания — нет. Таким образом, число размещений — это общее количество различных наборов при выборе k элементов из n без возвращения и с учетом порядка. Число сочетаний — общее количество различных наборов при выборе k элементов из n без возвращения и без учета порядка. Вычислить количество размещений и сочетаний можно следующим образом по довольно-таки простым формулам:
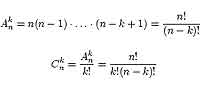

Распределения
К сожалению (а может быть, и наоборот), одной только комбинаторикой отделаться не удастся. Поэтому перейдем к более существенным с практической точки зрения вещам — к такому основополагающему для статистики понятию, как распределение. Для того, чтобы вспомнить, что такое распределение, обратимся, опять-таки, все к той же Википедии: "распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия". Конечно, Википедия, редактируемая всеми, кому не лень, довольно часто дает, скажем так, не слишком достоверную информацию. Однако здесь, как и в случае с комбинаторикой, все совершенно верно. Распределения делятся на два больших класса: дискретные и непрерывные. Дискретные распределения описывают свойства дискретных случайных величин; непрерывные, соответственно, непрерывных. Разных распределений, как дискретных, так и непрерывных, существует великое множество, однако практическое применение нашли сравнительно немногие из них. Среди дискретных наиболее часто встречаются в практических задачах распределения Бернулли, биномиальное, геометрическое, гипергеометрическое, логарифмическое, отрицательное биномиальное, Пуассона и равномерное. Из непрерывных — Колмогорова, Коши, Лапласа, Гаусса (оно также называется нормальным), равномерное, Стьюдента, Фишера, хи-квадрат и экспоненциальное. Конечно, мы с вами не будем сейчас рассматривать законы, описывающие каждое из этих распределений — это уже отдельная тема. Ознакомиться с ними, если возникнет такая необходимость, можно по любому учебнику и справочнику по математической статистике. Самый главный параметр, описывающий распределение — это плотность вероятности. С ее помощью можно вычислить вероятность нахождения случайной величины в заданном диапазоне. Для дискретной случайной величины вероятность находится с помощью суммирования, а для непрерывной — соответственно, с помощью интегрирования. При этом в последнем случае будет справедлива формула:
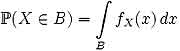
Здесь, конечно же P(x) — это собственно вероятность, а fx(x) — плотность вероятности. Так что, как видите, все довольно просто. В MathCAD есть встроенные функции, которые позволяют вычислить вероятность для разных распределений с заданными параметрами. Поскольку распределений много, и параметры у них у всех разные, мы с вами не будем пытаться догнать всех зайцев, а остановимся только на одном из них — на нормальном, или Гауссовом, распределении. Для моделирования случайных величин, чьи распределения описываются Гауссовой формулой, в MathCAD'е существует специальная функция — dnorm. У нее три параметра. Первый — это переменная x, которую пояснять, я так думаю, не нужно. Второй — это точка по оси x, на которую придется пик распределения (см. соответствующий рисунок). Третий — это дисперсия. Обратимся снова к Википедии: "дисперсия случайной величины — мера разброса данной случайной величины, т.е. ее отклонения от математического ожидания". Для нормального распределения математическим ожиданием является среднее для всех случайных величин значение. Работая с функцией dnorm, очень просто построить график для нормального распределения, который наверняка большинству из вас знаком еще по вузовскому курсу математики. Как видите, на графике действительно очень легко узнать характерный Гауссов контур, похожий на колокол. Вершина, как и было задано выше функцией dnorm, располагается в точке x = 5.

Что ж, пока что, пожалуй, хватит. Думаю, сведений вы пока и так получили достаточно, а комбинаторика и распределения — это действительно интересно, и вы можете самостоятельно поэкспериментировать со всем этим в MathCAD'е.
Выводы
Ну, что ж, по традиции подведем итоги всему тому, что мы уже сказали выше. Итогов, конечно, будет не слишком много, потому что и сказано было не так уж много… Но, тем не менее, без них статья была бы какой-то неполной и незаконченной, да и традиция, как ни крути, есть традиция. Итак, во-первых, как мы с вами, надеюсь, все-таки убедились, использовать MathCAD в статистических расчетах — совсем не такая плохая идея, как кому-то могло бы показаться. Во-вторых, работать с комбинаторными вычислениями в MathCAD'е действительно проще простого, и для этого вам даже не потребуется вручную вводить громоздкие формулы с факториалами. В-третьих, что касается разных распределений, то, хотя мы с вами рассмотрели только нормальное (Гауссово), это не означает, что MathCAD знает только его. Список всех остальных распределений и соответствующих им функций можно найти в справочной системе MathCAD'а. Попробуйте сделать примеры с какими-нибудь другими распределениями, и вы убедитесь в том, что MathCAD отлично умеет с ними работать.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 47 за 2008 год в рубрике soft


