MathCAD — это просто! Часть 29. Еще немного о программировании
Казалось бы, все, что может касаться программирования в математической среде MathCAD, о которой мы с вами говорим уже давным-давно на страницах КГ, мы уже разобрали по косточкам и разложили по полочкам. Однако первое впечатление обманчиво, поскольку программирование — настолько же сложная и многогранная дисциплина, насколько сложной и многогранной любая математическая дисциплина может быть. Именно поэтому сегодня мы продолжим (и, вероятно, закончим) разговор о программировании в MathCAD'е. Надеюсь, после того, как я подробно изложу вам оставшиеся вопросы данной темы, не останется никаких вопросов и неясностей.
В прошлый раз, напомню, мы говорили об отладке в MathCAD'е и об отладке написанных в этой среде программ в частности. А еще до этого мы с вами говорили о том, как бороться с ошибками. На самом деле, хотя мы уже много всего знаем о том, как это делать, есть еще некоторые моменты, которые по причине ограниченности размеров газетных полос остались за кадром. Вот на них мы с вами сейчас и обратим свои взоры.
Перехват ошибок в программах
Конечно, отладка — это замечательный способ поиска ошибок в программах, однако он замечательно работает только в тех случаях, когда ошибка статична и связана с тем, как именно написана сама программа. Однако это не до конца решает проблему ошибок динамических, то есть таких, которые проявляются в зависимости от каких-то внешних данных, с которыми работают программы. Если не совсем понятно, о чем я говорю, то приведу простой пример — к счастью, за ним далеко ходить не понадобится. Есть у нас, скажем, программа, которая обрабатывает данные из какого-то внешнего файла — скажем, в нем записаны значения сигнала какого-то измерительного прибора. И в процессе работы программа делит что-то на эти значения и затем еще каким-то образом далее, при этом нам, само собой, очень важен и интересен результат работы этой программы. При этом мы, сами понимаете, не можем никоим образом гарантировать отсутствие нулевых значений среди всего их спектра, который находится во внешнем файле. Таким образом, при встрече нашей программы с нулевым значением среди входных данных произойдет именно то, что всегда и происходит (и должно, в общем-то, происходить) при попытке деления на ноль — математическая среда MathCAD выдаст ошибку.
 Конечно, вы можете сказать, что это совсем не проблема, и можно вполне бороться с такими нулями с помощью обычных условных операторов if и otherwise, уже знакомых нам с вами. Что ж, если вы так скажете, то действительно будете совершенно правы, поскольку условные операторы позволяют самым что ни на есть удобным образом решить данную проблему. Однако это все будет хорошо, красиво и вообще действенно ровно до тех пор, пока мы будем в курсе, какие именно данные будут вызывать ошибку в программе. Ведь логика той же обработки данных может быть построена и таким образом, что ненулевые значения также могут вызвать сбой в дальнейших расчетах. Неужели необходимо предвидеть все ошибки, которые могут возникнуть, заранее? К счастью, есть способ избежать такого неприятного занятия, как перебор всех возможных ошибок, которые вообще могут возникнуть буквально на ровном месте. Поскольку существует специальный оператор, который позволяет эффективно с ними бороться, не прибегая к каким-то очень трудоемким методам. Называется этот оператор on error, и именно его использование мы с вами сейчас и обсудим.
Конечно, вы можете сказать, что это совсем не проблема, и можно вполне бороться с такими нулями с помощью обычных условных операторов if и otherwise, уже знакомых нам с вами. Что ж, если вы так скажете, то действительно будете совершенно правы, поскольку условные операторы позволяют самым что ни на есть удобным образом решить данную проблему. Однако это все будет хорошо, красиво и вообще действенно ровно до тех пор, пока мы будем в курсе, какие именно данные будут вызывать ошибку в программе. Ведь логика той же обработки данных может быть построена и таким образом, что ненулевые значения также могут вызвать сбой в дальнейших расчетах. Неужели необходимо предвидеть все ошибки, которые могут возникнуть, заранее? К счастью, есть способ избежать такого неприятного занятия, как перебор всех возможных ошибок, которые вообще могут возникнуть буквально на ровном месте. Поскольку существует специальный оператор, который позволяет эффективно с ними бороться, не прибегая к каким-то очень трудоемким методам. Называется этот оператор on error, и именно его использование мы с вами сейчас и обсудим.
Вы можете найти этот оператор на панели операторов, используемых при написании программ в MathCAD'е, рядом с оператором return. Однако с этим оператором тот, о котором мы сейчас с вами ведем разговор, имеет довольно мало общего. По своей работе оператор on error больше всего похож на условный оператор if — у него тоже есть два места для записи в них того, что должно происходить в различных случаях, и по своей структуре и функциям они практически идентичны аналогичным для оператора if. Слева от обсуждаемого оператора мы должны записать действие, которое должно быть выполнено в том, случае, если возникла ошибка, которая может возникнуть при выполнении действия, которое мы с вами должны записать с правой стороны от оператора. Как видите, общего с оператором if действительно много, однако отличие, являющееся принципиальным и кардинальным, заключается в том, что оператор on error выполняет записанное перед ним условие исключительно и только в тех случаях, когда обнаруживается какая- то ошибка в вычислении того выражения, которое записано после него. Давайте посмотрим на небольшой пример — программу, которая как раз и вычисляет обратные записанным в векторе величины и в случае появления нулевого значения пишет в результат бесконечность:
 Что ж, эта программа — действительно хороший пример того, какую пользу может принести оператор on error. Ведь без него ее выполнение остановилось бы уже на третьем элементе нашего вектора по той простой причине, что он является нулем. В принципе, можно придумать и более универсальный пример с самыми разными вычислительными ошибками, где оператор on error окажется еще полезнее, однако мы с вами этого делать сейчас не будем, потому что для того, чтобы изучить особенности применения данного оператора нам этого не требуется. Мы же лучше перейдем к еще одной теме, касающейся программирования в MathCAD'е, которая будет более чем полезной в практических расчетах с помощью этой мощной и удобной математической среды.
Что ж, эта программа — действительно хороший пример того, какую пользу может принести оператор on error. Ведь без него ее выполнение остановилось бы уже на третьем элементе нашего вектора по той простой причине, что он является нулем. В принципе, можно придумать и более универсальный пример с самыми разными вычислительными ошибками, где оператор on error окажется еще полезнее, однако мы с вами этого делать сейчас не будем, потому что для того, чтобы изучить особенности применения данного оператора нам этого не требуется. Мы же лучше перейдем к еще одной теме, касающейся программирования в MathCAD'е, которая будет более чем полезной в практических расчетах с помощью этой мощной и удобной математической среды.
Немного о рекурсии
В математике довольно часто используются рекуррентные соотношения, при которых n+1-й член какой-то последовательности вычисляется через n-й или даже несколько предыдущих. Классический пример рекуррентного соотношения — изучаемая еще в школе геометрическая прогрессия, где an + 1 = an.q, где q — знаменатель данной геометрической прогрессии. К чему я заговорил о рекуррентных соотношениях? А к тому, что в программировании принцип, лежащий в их основе, используется тоже весьма и весьма часто. Прием этот здесь называют рекурсией (как, впрочем, и везде). Как говорят программисты, чтобы понять рекурсию, нужно сначала понять рекурсию. Очень удачное выражение, целиком и полностью объясняющее суть рекурсии как понятия и метода. Это, кстати, называется лингвистической рекурсией. Но мы с вами, понятно, будем иметь дело совсем не с ней. Под рекурсией понимают такой способ написания программного кода, когда какая-то функция вызывает саму себя. Это может происходить не только прямо, но и опосредованно, то есть одна функция может вызывать другую, которая, в свою очередь, будет при этом вызывать первую. Такой случай принято называть сложной рекурсией. Приходилось слышать мнения, что использование рекурсии при написании программ снижает их стабильность, но, как правило, при грамотном использовании рекурсия способна существенно улучшить время, за которое выполняется программа, а также повысить читаемость программного кода. Впрочем, думаю, что нас с вами с точки зрения программирования в MathCAD'е рекурсия будет интересовать вовсе не по причине своих качеств в плане повышения читаемости кода, а именно по той самой причине, что она очень и очень удобна при написании некоторых программ и реализации рекуррентных алгоритмов. В общем-то, в практической реализации рекурсии нет совершенно ничего сложного, поскольку и сама по себе концепция рекурсивного программирования совершенно проста. Тем не менее, для того, чтобы эффективно и успешно работать с рекурсией в плане практическом, необходимо свыкнуться с тем, что функция вполне может вызвать саму себя в процессе собственного выполнения, и от этого ни она сама, ни кто-либо другой не станет чувствовать себя сильно хуже.
Давайте рассмотрим хрестоматийный пример, с которого, как правило, и начинается знакомство тех, кто изучает программирование, с рекурсией. Это вычисление факториала. Напомню на всякий случай, что факториал — это произведение последовательно стоящих натуральных чисел от единицы до n (например, 3! = 1.2.3). Рекурсивно факториал выражается так: n! = n.(n-1)!. Почему мы с вами будем рассматривать именно факториал? Дело в том, что эта функция просто отлично реализуется рекурсивно и при этом достаточно проста, чтобы не отвлекать вас от самой рекурсии на математические детали реализуемой функции. Давайте вместе взглянем на то, как реализуется функция вычисления факториала рекурсивным способом, а потом я дам несколько комментариев:
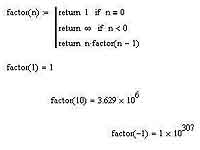 Итак, что мы видим? Мы рассматриваем в нашей программе, по большому счету, три различных варианта. Первый — это когда аргумент нашей функции равен нулю (по определению 0! = 1). Второй — это когда он равен отрицательному числу. В этом случае, понятное дело, мы факториал вычислить не можем и в качестве сигнала об ошибке возвращаем значение функции, равное бесконечности. Наконец, третий вариант — это положительный аргумент. Для него мы возвращаем значение согласно рекурсивной формуле n! = n.(n-1)!. Таким образом, наша программа будет вычислять, скажем, 3!, не как 1.2.3, а как 3.2.1. Когда она дойдет по цепочке от 3!, 2!, 1! до 0!, то выполнение закончится. Кстати, обратите внимание, что с помощью подобной реализации рекурсивного вычисления факториала мы избавляемся от необходимости проверять вычисление факториала дробного числа, поскольку при такой попытке наша программа неизбежно проскочит нужное ей для успешного завершения вычислений значение 0! и попытается вычислить факториал отрицательного числа, а этот случай мы уже проверили. Как видите, рекурсия просто замечательно подходит для замены циклических вычислений, местами позволяя решать их более изящно, чем при использовании более привычных пока что для вас циклов. Поэтому к рекурсии стоит привыкнуть, чтобы активно ею пользоваться — это замечательное средство, помогающее действительно быстро и эффективно решать очень многие, в том числе и довольно серьезные, задачи.
Итак, что мы видим? Мы рассматриваем в нашей программе, по большому счету, три различных варианта. Первый — это когда аргумент нашей функции равен нулю (по определению 0! = 1). Второй — это когда он равен отрицательному числу. В этом случае, понятное дело, мы факториал вычислить не можем и в качестве сигнала об ошибке возвращаем значение функции, равное бесконечности. Наконец, третий вариант — это положительный аргумент. Для него мы возвращаем значение согласно рекурсивной формуле n! = n.(n-1)!. Таким образом, наша программа будет вычислять, скажем, 3!, не как 1.2.3, а как 3.2.1. Когда она дойдет по цепочке от 3!, 2!, 1! до 0!, то выполнение закончится. Кстати, обратите внимание, что с помощью подобной реализации рекурсивного вычисления факториала мы избавляемся от необходимости проверять вычисление факториала дробного числа, поскольку при такой попытке наша программа неизбежно проскочит нужное ей для успешного завершения вычислений значение 0! и попытается вычислить факториал отрицательного числа, а этот случай мы уже проверили. Как видите, рекурсия просто замечательно подходит для замены циклических вычислений, местами позволяя решать их более изящно, чем при использовании более привычных пока что для вас циклов. Поэтому к рекурсии стоит привыкнуть, чтобы активно ею пользоваться — это замечательное средство, помогающее действительно быстро и эффективно решать очень многие, в том числе и довольно серьезные, задачи.
Выводы
Давайте по нашей доброй традиции подытожим все то, что было сказано выше. Сказано всего умного и не очень, конечно, было много (как, впрочем, и обычно), однако все, на самом деле, довольно просто, и при некоторой практике вы легко сможете со всем этим управиться в реальных задачах. Особое внимание в своих практических упражнения с MathCAD'ом, если вы твердо решили овладеть в совершенстве этой математической средой, мне кажется, стоит уделить именно рекурсии, поскольку это такой прием, без которого, на самом-то деле, жить местами бывает сложно, поэтому постарайтесь понять рекурсию, чтобы понять рекурсию. Ну, а в целом, конечно же, удачи вам в вашей работе с MathCAD'ом!
SF, spaceflyer@tut.by
В прошлый раз, напомню, мы говорили об отладке в MathCAD'е и об отладке написанных в этой среде программ в частности. А еще до этого мы с вами говорили о том, как бороться с ошибками. На самом деле, хотя мы уже много всего знаем о том, как это делать, есть еще некоторые моменты, которые по причине ограниченности размеров газетных полос остались за кадром. Вот на них мы с вами сейчас и обратим свои взоры.
Перехват ошибок в программах
Конечно, отладка — это замечательный способ поиска ошибок в программах, однако он замечательно работает только в тех случаях, когда ошибка статична и связана с тем, как именно написана сама программа. Однако это не до конца решает проблему ошибок динамических, то есть таких, которые проявляются в зависимости от каких-то внешних данных, с которыми работают программы. Если не совсем понятно, о чем я говорю, то приведу простой пример — к счастью, за ним далеко ходить не понадобится. Есть у нас, скажем, программа, которая обрабатывает данные из какого-то внешнего файла — скажем, в нем записаны значения сигнала какого-то измерительного прибора. И в процессе работы программа делит что-то на эти значения и затем еще каким-то образом далее, при этом нам, само собой, очень важен и интересен результат работы этой программы. При этом мы, сами понимаете, не можем никоим образом гарантировать отсутствие нулевых значений среди всего их спектра, который находится во внешнем файле. Таким образом, при встрече нашей программы с нулевым значением среди входных данных произойдет именно то, что всегда и происходит (и должно, в общем-то, происходить) при попытке деления на ноль — математическая среда MathCAD выдаст ошибку.

Вы можете найти этот оператор на панели операторов, используемых при написании программ в MathCAD'е, рядом с оператором return. Однако с этим оператором тот, о котором мы сейчас с вами ведем разговор, имеет довольно мало общего. По своей работе оператор on error больше всего похож на условный оператор if — у него тоже есть два места для записи в них того, что должно происходить в различных случаях, и по своей структуре и функциям они практически идентичны аналогичным для оператора if. Слева от обсуждаемого оператора мы должны записать действие, которое должно быть выполнено в том, случае, если возникла ошибка, которая может возникнуть при выполнении действия, которое мы с вами должны записать с правой стороны от оператора. Как видите, общего с оператором if действительно много, однако отличие, являющееся принципиальным и кардинальным, заключается в том, что оператор on error выполняет записанное перед ним условие исключительно и только в тех случаях, когда обнаруживается какая- то ошибка в вычислении того выражения, которое записано после него. Давайте посмотрим на небольшой пример — программу, которая как раз и вычисляет обратные записанным в векторе величины и в случае появления нулевого значения пишет в результат бесконечность:

Немного о рекурсии
В математике довольно часто используются рекуррентные соотношения, при которых n+1-й член какой-то последовательности вычисляется через n-й или даже несколько предыдущих. Классический пример рекуррентного соотношения — изучаемая еще в школе геометрическая прогрессия, где an + 1 = an.q, где q — знаменатель данной геометрической прогрессии. К чему я заговорил о рекуррентных соотношениях? А к тому, что в программировании принцип, лежащий в их основе, используется тоже весьма и весьма часто. Прием этот здесь называют рекурсией (как, впрочем, и везде). Как говорят программисты, чтобы понять рекурсию, нужно сначала понять рекурсию. Очень удачное выражение, целиком и полностью объясняющее суть рекурсии как понятия и метода. Это, кстати, называется лингвистической рекурсией. Но мы с вами, понятно, будем иметь дело совсем не с ней. Под рекурсией понимают такой способ написания программного кода, когда какая-то функция вызывает саму себя. Это может происходить не только прямо, но и опосредованно, то есть одна функция может вызывать другую, которая, в свою очередь, будет при этом вызывать первую. Такой случай принято называть сложной рекурсией. Приходилось слышать мнения, что использование рекурсии при написании программ снижает их стабильность, но, как правило, при грамотном использовании рекурсия способна существенно улучшить время, за которое выполняется программа, а также повысить читаемость программного кода. Впрочем, думаю, что нас с вами с точки зрения программирования в MathCAD'е рекурсия будет интересовать вовсе не по причине своих качеств в плане повышения читаемости кода, а именно по той самой причине, что она очень и очень удобна при написании некоторых программ и реализации рекуррентных алгоритмов. В общем-то, в практической реализации рекурсии нет совершенно ничего сложного, поскольку и сама по себе концепция рекурсивного программирования совершенно проста. Тем не менее, для того, чтобы эффективно и успешно работать с рекурсией в плане практическом, необходимо свыкнуться с тем, что функция вполне может вызвать саму себя в процессе собственного выполнения, и от этого ни она сама, ни кто-либо другой не станет чувствовать себя сильно хуже.
Давайте рассмотрим хрестоматийный пример, с которого, как правило, и начинается знакомство тех, кто изучает программирование, с рекурсией. Это вычисление факториала. Напомню на всякий случай, что факториал — это произведение последовательно стоящих натуральных чисел от единицы до n (например, 3! = 1.2.3). Рекурсивно факториал выражается так: n! = n.(n-1)!. Почему мы с вами будем рассматривать именно факториал? Дело в том, что эта функция просто отлично реализуется рекурсивно и при этом достаточно проста, чтобы не отвлекать вас от самой рекурсии на математические детали реализуемой функции. Давайте вместе взглянем на то, как реализуется функция вычисления факториала рекурсивным способом, а потом я дам несколько комментариев:
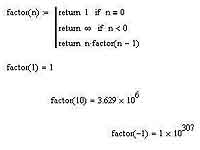
Выводы
Давайте по нашей доброй традиции подытожим все то, что было сказано выше. Сказано всего умного и не очень, конечно, было много (как, впрочем, и обычно), однако все, на самом деле, довольно просто, и при некоторой практике вы легко сможете со всем этим управиться в реальных задачах. Особое внимание в своих практических упражнения с MathCAD'ом, если вы твердо решили овладеть в совершенстве этой математической средой, мне кажется, стоит уделить именно рекурсии, поскольку это такой прием, без которого, на самом-то деле, жить местами бывает сложно, поэтому постарайтесь понять рекурсию, чтобы понять рекурсию. Ну, а в целом, конечно же, удачи вам в вашей работе с MathCAD'ом!
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 45 за 2008 год в рубрике soft


