MathCAD — это просто! Часть 25. Программирование в MathCAD: практика
В прошлый раз мы с вами начали разговор о таком полезном для каждого пользователя среды MathCAD навыке, как программирование. Начать-то, начали, да вот поговорить толком о нем, в общем-то, чего уж там скрывать, практически не успели. Это не очень здорово, потому что программирование вряд ли можно отнести к тем дисциплинам, в которых для успешной работы достаточно чисто теоретических знаний. Хотя, конечно, есть ли вообще такие дисциплины? Лично я в этом сомневаюсь — даже в теоретической физике есть много практических задач. Да и Маркс, которого многие из читателей наверняка изучали в ВУЗах, говорил, помнится, в свое время, что практика — критерий истины. Если мы будем только говорить о программировании, то такие разговоры вряд ли принесут хоть какую-то пользу. Поэтому гораздо полезнее рассмотреть программирование в такой мощной математической среде, как MathCAD, на конкретных примерах, чем долго рассказывать в общих чертах, что и как можно сделать. В общем, именно практикой мы с вами сейчас и займемся. Надеюсь, это будет для вас не только полезно, но и очень интересно.
Решение квадратного уравнения
Одна из первых программ, которую пишет человек, изучающий тот или иной язык программирования, — это программа, решающая квадратное уравнение. С одной стороны, алгоритм решения квадратных уравнений достаточно прост для того, чтобы не отвлекаться на него и сосредоточиться на особенностях изучаемого языка программирования; с другой стороны, этот алгоритм все же не сводится в тому, чтобы просто выполнить одну- единственную арифметическую операцию, которая сразу же даст нам результат. Конечно, программировать собственный алгоритм решения квадратных уравнений в одной из мощнейших математических сред может показаться безумством, ну, или, по крайней мере, это вряд ли будет достаточно рациональная трата времени. Что ж, если вы думаете так, то, наверное, стоит напомнить, что мы с вами вместе учимся работать в MathCAD, и время, потраченное на такую учебу, вряд ли можно будет назвать выкинутым на ветер. И, естественно, никто не предлагает всерьез писать альтернативную реализацию решателя квадратных уравнений — думаю, вы уже в курсе, что универсальная система решения алгебраических уравнений, встроенная в MathCAD, способна справиться и с куда более сложными задачами. В общем, давайте сначала посмотрим на то, как можно решать в MathCAD'е квадратные уравнения, прибегнув к программированию, а потом уже обсудим детали этого решения:
Итак, давайте будем разбираться. Как видите, для удобства коэффициенты объявлены в виде обычных переменных MathCAD'а. Такие переменные могут использоваться как в самой программе, так и вне ее — по этой причине они называются внешними. Когда переменные объявляются в самой программе, то для нее они являются внутренними и, как несложно догадаться, за ее рамками никакой силы не имеют. В нашей программе всего две строки. Первая из них, как несложно догадаться, выполнится в том случае, если коэффициент при старшем члене в нашем уравнении будет равен нулю. Тогда оно из квадратного обратится в линейное, и решать его нужно будет уже с использованием совсем других формул. Обратите внимание, что в MathCAD'е результат выполнения условия записывается до самого условия — это, вообще говоря, совсем не характерно для большинства языков программирования, однако благодаря этому текст программы смотрится естественнее с точки зрения английского языка. Оператор return используется для того, чтобы вывести какое-либо выражение как результат выполнения нашей программы — если бы мы его не использовали, то и после знака равно ничего бы не было выведено. Вторая строка программы содержит в себе решение именно квадратного уравнения, то есть в ней рассматривается случай, когда коэффициент при старшем члене не равен нулю. Заметьте, пожалуйста, что оператор otherwise используется только после условной конструкции с оператором if, при отсутствии которой он становится совершенно бессмысленным. Этот оператор относится к последней условной конструкции, если иное не указано с помощью расстановки иерархии операторов в программе.
Здесь следует также заметить, что операторы необходимо вводить с помощью соответствующей панели инструментов, о которой я довольно-таки подробно рассказывал в предыдущей статье серии "MathCAD — это просто!", либо же с помощью соответствующих им горячих клавиатурных комбинаций клавиш. Дело в том, что, если вы попробуете вводить операторы в программе, просто набирая их на клавиатуре (тот же if, в принципе, набрать по буквам даже и быстрее), то MathCAD воспримет их как переменные и не будет с ними работать должным образом. Собственно говоря, как вы видите, внизу для контроля правильности написанной нами программы используется оператор solve, решающий точно такое же квадратное уравнение. Чтобы убедиться в том, что наша мини-программа успешно справляется с уравнениями и в тех случаях, когда они вырождаются в линейные, и что все работает именно так, как первоначально и было задумано, изменим значение переменной a на нулевое и посмотрим, что из этого у нас с вами получится: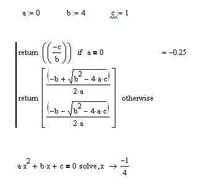
Что ж, как видите, все получилось очень даже и неплохо, и все работает именно так, как мы с вами, собственно говоря, и предполагали. Однако решение квадратных уравнений, каким бы удачным примером оно ни было, не охватывает всех операторов на панели программирования MathCAD, которые могут пригодиться вам в дальнейшем. Поэтому, пожалуй, имеет смысл заканчивать разбираться с дифференциальными уравнениями и переходить к следующим программам — таким же простым, но не менее познавательным, чем та, которую мы с вами только что успешно рассмотрели.
Транспонирование матриц
Давайте рассмотрим еще один просто-таки предельно простой пример, который также проще простого реализуется с помощью встроенных операторов MathCAD. Тем не менее, транспонирование матриц позволяет очень удобным образом проиллюстрировать те приемы программирования, которые мы не затрагивали еще в нашем с вами первом примере с решением квадратного уравнения. Как водится, давайте для начала посмотрим на программный код, с помощью которого можно реализовать в MathCAD'е транспонирование матрицы, а затем уже будем разбираться, что и как он делает: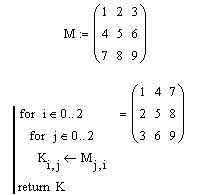
Что ж, как видите, уже с самого начала программный код преподносит нам некоторые сюрпризы — в нем сходу встречается доселе неизвестная нам конструкция for. Но на самом деле она очень проста и крайне часто употребляема, а потому бояться ее совсем не нужно — нужно разобраться. Что она делает? Никакого секрета, собственного говоря, из этого никто не делает. Эта конструкция используется для организации цикла с заранее заданным числом итераций (сиречь повторений). Конструкция эта очень распространена и с небольшим числом вариаций используется практически во всех более- менее распространенных языках программирования. Благодаря ей в ходе выполнения программы переменная, которая указана в этой конструкции (в нашем случае такими переменными будут i и j) "пробегает" весь диапазон значений, указанный также в этой конструкции, с единичным шагом. Обратите также внимание, что нумерация элементов матрицы начинается не с единицы, а с нуля — то есть верхний левый элемент имеет индекс 0, 0, а не 1, 1. Поскольку наши конструкции for являются вложенными, то для каждой итерации переменной i выполняется три итерации переменной j. Вложенность в MathCAD'е, как несложно, в общем-то, заметить, отображается с помощью отступов. В каждой итерации для переменной j выполняется собственно операция транспонирования — то есть каждому i,j-му элементу матрицы K присваивается j,i-й элемент нашей исходной матрицы M. Здесь мы встречаемся с еще одним доселе незнакомым нам с вами приемом программирования — операцией присваивания значения. Во многих языках программирования для того, чтобы присвоить переменной какое-либо значение, требуется сначала ее объявить. В общем-то, в "большом" программирование это требование вполне обоснованно, однако программирование в MathCAD, сами понимаете, имеет свою специфику, а потому тип переменной, если она не задана нигде выше, определяется автоматически. Как видите, нам не пришлось нигде и никак объяснять MathCAD'у, что K — это матрица; более того, нам даже не пришлось указывать нигде ее размеры. Разработчики этой мощной математической среды сумели сделать ее по-настоящему удобной для людей, далеких от программирования, даже тогда, когда к нему все же приходится обращаться.
Стоит сказать несколько слов и по поводу того, какими особенностями обладает операция присваивания. Присвоить можно что угодно и как угодно при условии совпадения типов присваиваемого значения и той переменной, которой вы его желаете присвоить. Поэтому совершенно нормальной (и, более того, отнюдь не редкой) является ситуация, когда конструкция вида a < a + 1 кажется совершенно бессмысленной для новичка в программировании. К счастью, в MathCAD'е для обозначения присваивания не используется знак равенства, поскольку в тех языках программирования, где используется именно он, подобная конструкция выглядит поначалу совершенно дико. Еще одна особенность кода этой программы состоит в том, что, если вы попробуете использовать переменную K после самой программы, то результат будет не вполне ожидаемым: вы можете наблюдать его на соответствующей иллюстрации. Так происходит по той причине, что переменная K является внутренней переменной для той программы, о которой мы сейчас ведем разговор, а потому вне программы мы и не можем никак ее использовать — фактически K в программе и K вне ее являются с точки зрения MathCAD'а в данном случае разными переменными.
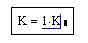
Выводы
Давайте подытожим то, о чем мы сегодня говорили. Как видите, MathCAD — настолько мощная среда, что в ней даже такие простые операции, как транспонирование матриц и решение квадратных уравнений, можно выполнить несколькими способами. Конечно, в этих случаях прибегать к программированию не совсем целесообразно, однако моей задачей было познакомить вас с основными операторами, используемыми при программировании в MathCAD'е, и именно потому я обратился к столь простым примерам. Надеюсь, вам они тоже не показались сложными, и вы извлечете из них пользу. Программирование — замечательное занятие, и, если вы не умеете программировать, думаю, стоит найти немного свободного времени, чтобы его изучить. Пусть те простые задачи, которые мы обсуждаем, разговаривая о программировании в MathCAD'е, откроют вам дверь в удивительный мир программирования!
SF, spaceflyer@tut.by
Решение квадратного уравнения
Одна из первых программ, которую пишет человек, изучающий тот или иной язык программирования, — это программа, решающая квадратное уравнение. С одной стороны, алгоритм решения квадратных уравнений достаточно прост для того, чтобы не отвлекаться на него и сосредоточиться на особенностях изучаемого языка программирования; с другой стороны, этот алгоритм все же не сводится в тому, чтобы просто выполнить одну- единственную арифметическую операцию, которая сразу же даст нам результат. Конечно, программировать собственный алгоритм решения квадратных уравнений в одной из мощнейших математических сред может показаться безумством, ну, или, по крайней мере, это вряд ли будет достаточно рациональная трата времени. Что ж, если вы думаете так, то, наверное, стоит напомнить, что мы с вами вместе учимся работать в MathCAD, и время, потраченное на такую учебу, вряд ли можно будет назвать выкинутым на ветер. И, естественно, никто не предлагает всерьез писать альтернативную реализацию решателя квадратных уравнений — думаю, вы уже в курсе, что универсальная система решения алгебраических уравнений, встроенная в MathCAD, способна справиться и с куда более сложными задачами. В общем, давайте сначала посмотрим на то, как можно решать в MathCAD'е квадратные уравнения, прибегнув к программированию, а потом уже обсудим детали этого решения:

Итак, давайте будем разбираться. Как видите, для удобства коэффициенты объявлены в виде обычных переменных MathCAD'а. Такие переменные могут использоваться как в самой программе, так и вне ее — по этой причине они называются внешними. Когда переменные объявляются в самой программе, то для нее они являются внутренними и, как несложно догадаться, за ее рамками никакой силы не имеют. В нашей программе всего две строки. Первая из них, как несложно догадаться, выполнится в том случае, если коэффициент при старшем члене в нашем уравнении будет равен нулю. Тогда оно из квадратного обратится в линейное, и решать его нужно будет уже с использованием совсем других формул. Обратите внимание, что в MathCAD'е результат выполнения условия записывается до самого условия — это, вообще говоря, совсем не характерно для большинства языков программирования, однако благодаря этому текст программы смотрится естественнее с точки зрения английского языка. Оператор return используется для того, чтобы вывести какое-либо выражение как результат выполнения нашей программы — если бы мы его не использовали, то и после знака равно ничего бы не было выведено. Вторая строка программы содержит в себе решение именно квадратного уравнения, то есть в ней рассматривается случай, когда коэффициент при старшем члене не равен нулю. Заметьте, пожалуйста, что оператор otherwise используется только после условной конструкции с оператором if, при отсутствии которой он становится совершенно бессмысленным. Этот оператор относится к последней условной конструкции, если иное не указано с помощью расстановки иерархии операторов в программе.
Здесь следует также заметить, что операторы необходимо вводить с помощью соответствующей панели инструментов, о которой я довольно-таки подробно рассказывал в предыдущей статье серии "MathCAD — это просто!", либо же с помощью соответствующих им горячих клавиатурных комбинаций клавиш. Дело в том, что, если вы попробуете вводить операторы в программе, просто набирая их на клавиатуре (тот же if, в принципе, набрать по буквам даже и быстрее), то MathCAD воспримет их как переменные и не будет с ними работать должным образом. Собственно говоря, как вы видите, внизу для контроля правильности написанной нами программы используется оператор solve, решающий точно такое же квадратное уравнение. Чтобы убедиться в том, что наша мини-программа успешно справляется с уравнениями и в тех случаях, когда они вырождаются в линейные, и что все работает именно так, как первоначально и было задумано, изменим значение переменной a на нулевое и посмотрим, что из этого у нас с вами получится:

Что ж, как видите, все получилось очень даже и неплохо, и все работает именно так, как мы с вами, собственно говоря, и предполагали. Однако решение квадратных уравнений, каким бы удачным примером оно ни было, не охватывает всех операторов на панели программирования MathCAD, которые могут пригодиться вам в дальнейшем. Поэтому, пожалуй, имеет смысл заканчивать разбираться с дифференциальными уравнениями и переходить к следующим программам — таким же простым, но не менее познавательным, чем та, которую мы с вами только что успешно рассмотрели.
Транспонирование матриц
Давайте рассмотрим еще один просто-таки предельно простой пример, который также проще простого реализуется с помощью встроенных операторов MathCAD. Тем не менее, транспонирование матриц позволяет очень удобным образом проиллюстрировать те приемы программирования, которые мы не затрагивали еще в нашем с вами первом примере с решением квадратного уравнения. Как водится, давайте для начала посмотрим на программный код, с помощью которого можно реализовать в MathCAD'е транспонирование матрицы, а затем уже будем разбираться, что и как он делает:
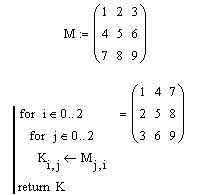
Что ж, как видите, уже с самого начала программный код преподносит нам некоторые сюрпризы — в нем сходу встречается доселе неизвестная нам конструкция for. Но на самом деле она очень проста и крайне часто употребляема, а потому бояться ее совсем не нужно — нужно разобраться. Что она делает? Никакого секрета, собственного говоря, из этого никто не делает. Эта конструкция используется для организации цикла с заранее заданным числом итераций (сиречь повторений). Конструкция эта очень распространена и с небольшим числом вариаций используется практически во всех более- менее распространенных языках программирования. Благодаря ей в ходе выполнения программы переменная, которая указана в этой конструкции (в нашем случае такими переменными будут i и j) "пробегает" весь диапазон значений, указанный также в этой конструкции, с единичным шагом. Обратите также внимание, что нумерация элементов матрицы начинается не с единицы, а с нуля — то есть верхний левый элемент имеет индекс 0, 0, а не 1, 1. Поскольку наши конструкции for являются вложенными, то для каждой итерации переменной i выполняется три итерации переменной j. Вложенность в MathCAD'е, как несложно, в общем-то, заметить, отображается с помощью отступов. В каждой итерации для переменной j выполняется собственно операция транспонирования — то есть каждому i,j-му элементу матрицы K присваивается j,i-й элемент нашей исходной матрицы M. Здесь мы встречаемся с еще одним доселе незнакомым нам с вами приемом программирования — операцией присваивания значения. Во многих языках программирования для того, чтобы присвоить переменной какое-либо значение, требуется сначала ее объявить. В общем-то, в "большом" программирование это требование вполне обоснованно, однако программирование в MathCAD, сами понимаете, имеет свою специфику, а потому тип переменной, если она не задана нигде выше, определяется автоматически. Как видите, нам не пришлось нигде и никак объяснять MathCAD'у, что K — это матрица; более того, нам даже не пришлось указывать нигде ее размеры. Разработчики этой мощной математической среды сумели сделать ее по-настоящему удобной для людей, далеких от программирования, даже тогда, когда к нему все же приходится обращаться.
Стоит сказать несколько слов и по поводу того, какими особенностями обладает операция присваивания. Присвоить можно что угодно и как угодно при условии совпадения типов присваиваемого значения и той переменной, которой вы его желаете присвоить. Поэтому совершенно нормальной (и, более того, отнюдь не редкой) является ситуация, когда конструкция вида a < a + 1 кажется совершенно бессмысленной для новичка в программировании. К счастью, в MathCAD'е для обозначения присваивания не используется знак равенства, поскольку в тех языках программирования, где используется именно он, подобная конструкция выглядит поначалу совершенно дико. Еще одна особенность кода этой программы состоит в том, что, если вы попробуете использовать переменную K после самой программы, то результат будет не вполне ожидаемым: вы можете наблюдать его на соответствующей иллюстрации. Так происходит по той причине, что переменная K является внутренней переменной для той программы, о которой мы сейчас ведем разговор, а потому вне программы мы и не можем никак ее использовать — фактически K в программе и K вне ее являются с точки зрения MathCAD'а в данном случае разными переменными.
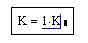
Выводы
Давайте подытожим то, о чем мы сегодня говорили. Как видите, MathCAD — настолько мощная среда, что в ней даже такие простые операции, как транспонирование матриц и решение квадратных уравнений, можно выполнить несколькими способами. Конечно, в этих случаях прибегать к программированию не совсем целесообразно, однако моей задачей было познакомить вас с основными операторами, используемыми при программировании в MathCAD'е, и именно потому я обратился к столь простым примерам. Надеюсь, вам они тоже не показались сложными, и вы извлечете из них пользу. Программирование — замечательное занятие, и, если вы не умеете программировать, думаю, стоит найти немного свободного времени, чтобы его изучить. Пусть те простые задачи, которые мы обсуждаем, разговаривая о программировании в MathCAD'е, откроют вам дверь в удивительный мир программирования!
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 39 за 2008 год в рубрике soft


