MathCAD — это просто! Часть 20. Страх и ужас: дифференциальные уравнения
Если вы спросите студентов естественнонаучных и технических специальностей, какую часть высшей математики они "любят" больше всего, то в трех четвертях случаев в ответ услышите именно "дифференциальные уравнения". И действительно, именно диффуры становятся нередко тем самым гранитом науки, который студентам приходится в буквальном смысле грызть. Впрочем, грызть его в силу применения диффуров в различных практических отраслях человеческой деятельности приходится и специалистам, ВУЗ уже давно закончившим. Но им, в отличие от студентов, можно немного облегчить себе жизнь — даже, пожалуй, не немного, а весьма ощутимо — благодаря тому, что такой мощный математический пакет, как MathCAD, поддерживает решение дифференциальных уравнений ничуть не хуже, чем многие другие операции, о которых мы с вами говорили. Студентам, конечно, MathCAD тоже может помочь, но, увы, не при изучении дифференциальных уравнений — вряд ли преподаватели будут в восторге, если принести распечатанное решение такого уравнения в MathCAD'е. Впрочем, не суть важно, студент вы или нет, ведь если вы решили постичь премудрости работы с дифференциальными уравнениями в среде MathCAD — значит, вам зачем-то это нужно…
Краткий ликбез
Как и в прошлый раз, когда мы говорили с вами о такой важной части математики, как комплексные числа, я позволю себе небольшое отступление от темы работы в MathCAD'е для рассказа о том, что же такое, собственно говоря, эти самые дифференциальные уравнения, и почему они вызывают ужас у студентов. В справочнике по математике можно найти определение вроде: "дифференциальным уравнением называют уравнение вида f(y1, y2, …, yn, ?y1/?x1, …, ?y1/?xm, … ?myn/?x1…?xm, x1, …, xm) = 0, где ?jyi/?xk…?xk+j — производная функции yi под аргументам xk…xk+j". На самом же деле, несмотря на то, что написанное выше определение может быть не слишком удобным для восприятия — все довольно просто. Дифференциальное уравнение — это такое уравнение, в котором есть одна или несколько функций и их производные. И задача того, кто решает такое уравнение, — найти все функции, при котором бы оно превращалось в тождество (было справедливым при любом значении аргумента).
Выделяют два больших класса дифференциальных уравнений: обыкновенные дифференциальные уравнения и уравнения в частных производных. В обыкновенных дифференциальных уравнениях фигурируют функции одной переменной, а потому все производные в них полные. Дифференциальные уравнения в частных производных, напротив, содержат в себе функции нескольких переменных и частные производные этих функций по разным переменным. Понятно, что решать обыкновенные дифференциальные уравнения куда проще, но встречаются они, к сожалению, реже, потому что все более-менее важные обыкновенные дифференциальные уравнения давным-давно решены, а их решения записаны в справочники и учебники по математике и физике. Разработаны специальные приемы, которые позволяют хорошо и быстро решать отдельные типы дифференциальных уравнений. Тем не менее, несмотря на то, что эти уравнения известны человечеству уже не одну сотню лет, до сих пор не существует универсального способа, позволяющего аналитически решить любое дифференциальное уравнение. Поэтому при решении этих уравнений в среде MathCAD лучше тоже заранее подготовиться к тому, что далеко не все из того, что вы захотите решить с помощью этого математического пакета, и в самом деле будет решаться. Сейчас мы с вами рассмотрим разные типы дифференциальных уравнений, которые решаются аналитически с применением к ним различных подходов. А в следующий раз посмотрим на то, как можно численно решать дифференциальные уравнения, не теряя времени на определение того, к какому именно типу они принадлежат.
Интегрирование
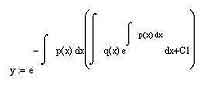 В конечном счете решение дифференциального уравнения рано или поздно так или иначе явно или неявно, но сводится к интегрированию каких-либо функций. А потому во многих случаях имеет смысл сразу, с места в карьер, приступать к интегрированию. Давайте рассмотрим уравнение вида dy/dx = p(x)*y + q(x), где p и q — некоторые интегрируемые функции. Общее решение подобного вида уравнений вы можете увидеть на приведенной ниже формуле:
В конечном счете решение дифференциального уравнения рано или поздно так или иначе явно или неявно, но сводится к интегрированию каких-либо функций. А потому во многих случаях имеет смысл сразу, с места в карьер, приступать к интегрированию. Давайте рассмотрим уравнение вида dy/dx = p(x)*y + q(x), где p и q — некоторые интегрируемые функции. Общее решение подобного вида уравнений вы можете увидеть на приведенной ниже формуле:
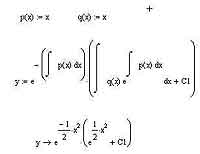 Собственно, эта формула — уже фактически готовое решение дифференциального уравнения (напомню, что C1 — это некоторая константа, которая обозначена так потому, что идентификаторы C и c уже заняты стандартными переменными среды MathCAD). Если вместо p(x) и q(x) мы подставим какие- либо конкретные значения коэффициентов, фигурирующих в уравнении, то, если все интегралы окажутся берущимися, среда MathCAD самостоятельно сможет рассчитать решение этого уравнения. Давайте посмотрим на примере, как это может выглядеть:
Собственно, эта формула — уже фактически готовое решение дифференциального уравнения (напомню, что C1 — это некоторая константа, которая обозначена так потому, что идентификаторы C и c уже заняты стандартными переменными среды MathCAD). Если вместо p(x) и q(x) мы подставим какие- либо конкретные значения коэффициентов, фигурирующих в уравнении, то, если все интегралы окажутся берущимися, среда MathCAD самостоятельно сможет рассчитать решение этого уравнения. Давайте посмотрим на примере, как это может выглядеть:
Аналогичным образом можно поступить, найдя в справочнике формулы для некоторых других видов дифференциальных уравнений. Правда, стоит помнить, что результаты интегрирования, выдаваемые символьным процессором MathCAD'а, стоит перепроверять — но сделать это совсем не сложно путем простой подстановки. А сейчас мы поговорим о другом способе аналитического решения уравнений, который более универсален и требует применения некоторых операторов символьного вычисления, о которых мы с вами не так давно говорили.
Операционное исчисление
Не так давно мы говорили о прямом и обратном преобразованиях Лапласа, которые очень активно применяются при решении дифференциальных уравнений методами операционного исчисления. Операционное исчисление, конечно же, тоже не гарантирует вам того, что ваше уравнение обязательно решится, однако это более универсальный способ, чем использование отдельных формул, специфических для каждого из видов обыкновенных дифференциальных уравнений. Хотя я уже рассказывал о сути операционного исчисления, тем не менее, полагаю, что, если повторю свой рассказ, вряд ли это кому-то повредит. Преобразованием Лапласа мы получаем новые функции комплексных переменных, которые называются изображениями (в то время, как старые функции действительных переменных называются оригиналами). Новые функции образуют между собой новое уравнение, называемое операторным — в отличие от старого, дифференциального, оно алгебраическое. После решения операторного уравнения, которое решить значительно проще, чем исходное, можно вернуться к старым переменным, и получить решение исходного дифференциального уравнения.
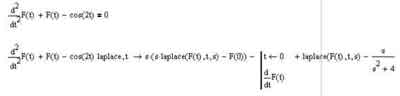 Стоит, конечно же, сказать, что операционное исчисление — тоже совсем не панацея, поскольку оно накладывает ряд ограничений на функцию, подвергаемую преобразованию Лапласа. Первое из этих ограничений — необходимость непрерывности функции (допускается наличие только конечного числа разрывов первого рода). Второе ограничение — функция должна иметь нулевые значения для всех отрицательных значений аргумента. Ну и, наконец, функция должна возрастать медленнее экспоненты (впрочем, последнее условие выполнить сравнительно несложно, поскольку на самом деле оно несколько сложнее, чем я его вам изложил). Что ж, давайте посмотрим, как мы можем применить операционное исчисление к дифференциальным уравнениям в MathCAD'е. Для начала выберем уравнение, которое будем решать. Пусть это будет, например, d2F(t)/dx2 + F(t) — cos(2t) = 0. Левую часть этого уравнения нужно подвергнуть преобразованию Лапласа, то есть, говоря по-русски, действию оператора laplace. То, что получится в итоге, можно увидеть ниже.
Стоит, конечно же, сказать, что операционное исчисление — тоже совсем не панацея, поскольку оно накладывает ряд ограничений на функцию, подвергаемую преобразованию Лапласа. Первое из этих ограничений — необходимость непрерывности функции (допускается наличие только конечного числа разрывов первого рода). Второе ограничение — функция должна иметь нулевые значения для всех отрицательных значений аргумента. Ну и, наконец, функция должна возрастать медленнее экспоненты (впрочем, последнее условие выполнить сравнительно несложно, поскольку на самом деле оно несколько сложнее, чем я его вам изложил). Что ж, давайте посмотрим, как мы можем применить операционное исчисление к дифференциальным уравнениям в MathCAD'е. Для начала выберем уравнение, которое будем решать. Пусть это будет, например, d2F(t)/dx2 + F(t) — cos(2t) = 0. Левую часть этого уравнения нужно подвергнуть преобразованию Лапласа, то есть, говоря по-русски, действию оператора laplace. То, что получится в итоге, можно увидеть ниже.
Это не совсем подходящее выражение для его последующего "скармливания" оператору solve, а потому надо кое-что поменять. А именно — записать в человеческом виде начальные значения функции F и ее производной F(0) и F'(0) (мы их запишем как F0 и Fd0 соответственно). Также нужно записать как-то покороче выражение laplace(F(t),t,s), которое мы, следуя традициям операционных методов, назовем буквой z. Это выражение — та переменная, относительно которой мы будем решать операторное уравнение. Вот так и должно выглядеть его решение, если вы сделали все так, как я вам говорил:
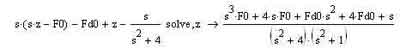 Теперь дело за малым — нам нужно выполнить обратное преобразование Лапласа для того, чтобы от изображения перейти назад к оригиналу, то есть фактически и получить решение нашего исходного дифференциального уравнения d2F(t)/dx2 + F(t) — cos(2t) = 0. Для этого, если вы помните, нужно использовать оператор invlaplace, о котором мы говорили тогда же, когда разбирали и все остальные операторы символьных преобразований. Вот что у нас с вами должно получиться после того, как мы это сделаем:
Теперь дело за малым — нам нужно выполнить обратное преобразование Лапласа для того, чтобы от изображения перейти назад к оригиналу, то есть фактически и получить решение нашего исходного дифференциального уравнения d2F(t)/dx2 + F(t) — cos(2t) = 0. Для этого, если вы помните, нужно использовать оператор invlaplace, о котором мы говорили тогда же, когда разбирали и все остальные операторы символьных преобразований. Вот что у нас с вами должно получиться после того, как мы это сделаем:
 Конечно, полученное решение с большой натяжкой можно назвать не то что изящным, но даже и просто сколь-нибудь приличным, потому что к нему стоит применить еще некоторые операторы. Какие? Этот вопрос оставим вам на самостоятельное изучение — вернее сказать, даже не на изучение, а на повторение, поскольку обо всех операторах символьных вычислений, какие только могут вам потребоваться, я уже рассказывал в серии "MathCAD — это просто!". Так что, если вы внимательно читали каждую из статей, то у вас не будет проблем с дальнейшим приведением этого выражения в приличный вид.
Конечно, полученное решение с большой натяжкой можно назвать не то что изящным, но даже и просто сколь-нибудь приличным, потому что к нему стоит применить еще некоторые операторы. Какие? Этот вопрос оставим вам на самостоятельное изучение — вернее сказать, даже не на изучение, а на повторение, поскольку обо всех операторах символьных вычислений, какие только могут вам потребоваться, я уже рассказывал в серии "MathCAD — это просто!". Так что, если вы внимательно читали каждую из статей, то у вас не будет проблем с дальнейшим приведением этого выражения в приличный вид.
Выводы
Что ж, как видите, MathCAD в очередной раз оказался силен — именно поэтому я не устаю петь дифирамбы этому пакету как мощному математическому инструменту, удобному, ко всему прочему, в практической работе. Решать дифференциальные уравнения с помощь MathCAD'а, как я уже говорил, совсем и не сложно — даже если сейчас вам показалось, что процесс их решения занимает много времени, уверяю вас, это мелочи по сравнению с тем временем, которое вы бы затратили на то, чтобы решить их вручную. Конечно, аналитический способ решения не дает вам 100- процентной гарантии успеха, как, впрочем, и всегда, но зато можно воспользоваться решением численным. Но это, как говорится, уже совсем другая история…
SF, spaceflyer@tut.by
Краткий ликбез
Как и в прошлый раз, когда мы говорили с вами о такой важной части математики, как комплексные числа, я позволю себе небольшое отступление от темы работы в MathCAD'е для рассказа о том, что же такое, собственно говоря, эти самые дифференциальные уравнения, и почему они вызывают ужас у студентов. В справочнике по математике можно найти определение вроде: "дифференциальным уравнением называют уравнение вида f(y1, y2, …, yn, ?y1/?x1, …, ?y1/?xm, … ?myn/?x1…?xm, x1, …, xm) = 0, где ?jyi/?xk…?xk+j — производная функции yi под аргументам xk…xk+j". На самом же деле, несмотря на то, что написанное выше определение может быть не слишком удобным для восприятия — все довольно просто. Дифференциальное уравнение — это такое уравнение, в котором есть одна или несколько функций и их производные. И задача того, кто решает такое уравнение, — найти все функции, при котором бы оно превращалось в тождество (было справедливым при любом значении аргумента).
Выделяют два больших класса дифференциальных уравнений: обыкновенные дифференциальные уравнения и уравнения в частных производных. В обыкновенных дифференциальных уравнениях фигурируют функции одной переменной, а потому все производные в них полные. Дифференциальные уравнения в частных производных, напротив, содержат в себе функции нескольких переменных и частные производные этих функций по разным переменным. Понятно, что решать обыкновенные дифференциальные уравнения куда проще, но встречаются они, к сожалению, реже, потому что все более-менее важные обыкновенные дифференциальные уравнения давным-давно решены, а их решения записаны в справочники и учебники по математике и физике. Разработаны специальные приемы, которые позволяют хорошо и быстро решать отдельные типы дифференциальных уравнений. Тем не менее, несмотря на то, что эти уравнения известны человечеству уже не одну сотню лет, до сих пор не существует универсального способа, позволяющего аналитически решить любое дифференциальное уравнение. Поэтому при решении этих уравнений в среде MathCAD лучше тоже заранее подготовиться к тому, что далеко не все из того, что вы захотите решить с помощью этого математического пакета, и в самом деле будет решаться. Сейчас мы с вами рассмотрим разные типы дифференциальных уравнений, которые решаются аналитически с применением к ним различных подходов. А в следующий раз посмотрим на то, как можно численно решать дифференциальные уравнения, не теряя времени на определение того, к какому именно типу они принадлежат.
Интегрирование
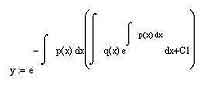
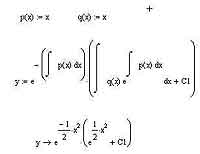
Аналогичным образом можно поступить, найдя в справочнике формулы для некоторых других видов дифференциальных уравнений. Правда, стоит помнить, что результаты интегрирования, выдаваемые символьным процессором MathCAD'а, стоит перепроверять — но сделать это совсем не сложно путем простой подстановки. А сейчас мы поговорим о другом способе аналитического решения уравнений, который более универсален и требует применения некоторых операторов символьного вычисления, о которых мы с вами не так давно говорили.
Операционное исчисление
Не так давно мы говорили о прямом и обратном преобразованиях Лапласа, которые очень активно применяются при решении дифференциальных уравнений методами операционного исчисления. Операционное исчисление, конечно же, тоже не гарантирует вам того, что ваше уравнение обязательно решится, однако это более универсальный способ, чем использование отдельных формул, специфических для каждого из видов обыкновенных дифференциальных уравнений. Хотя я уже рассказывал о сути операционного исчисления, тем не менее, полагаю, что, если повторю свой рассказ, вряд ли это кому-то повредит. Преобразованием Лапласа мы получаем новые функции комплексных переменных, которые называются изображениями (в то время, как старые функции действительных переменных называются оригиналами). Новые функции образуют между собой новое уравнение, называемое операторным — в отличие от старого, дифференциального, оно алгебраическое. После решения операторного уравнения, которое решить значительно проще, чем исходное, можно вернуться к старым переменным, и получить решение исходного дифференциального уравнения.
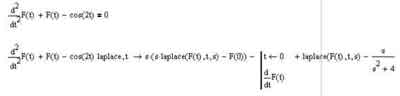
Это не совсем подходящее выражение для его последующего "скармливания" оператору solve, а потому надо кое-что поменять. А именно — записать в человеческом виде начальные значения функции F и ее производной F(0) и F'(0) (мы их запишем как F0 и Fd0 соответственно). Также нужно записать как-то покороче выражение laplace(F(t),t,s), которое мы, следуя традициям операционных методов, назовем буквой z. Это выражение — та переменная, относительно которой мы будем решать операторное уравнение. Вот так и должно выглядеть его решение, если вы сделали все так, как я вам говорил:
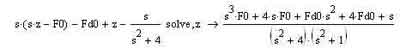

Выводы
Что ж, как видите, MathCAD в очередной раз оказался силен — именно поэтому я не устаю петь дифирамбы этому пакету как мощному математическому инструменту, удобному, ко всему прочему, в практической работе. Решать дифференциальные уравнения с помощь MathCAD'а, как я уже говорил, совсем и не сложно — даже если сейчас вам показалось, что процесс их решения занимает много времени, уверяю вас, это мелочи по сравнению с тем временем, которое вы бы затратили на то, чтобы решить их вручную. Конечно, аналитический способ решения не дает вам 100- процентной гарантии успеха, как, впрочем, и всегда, но зато можно воспользоваться решением численным. Но это, как говорится, уже совсем другая история…
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 34 за 2008 год в рубрике soft


