MathCAD — это просто! Часть 17. Снова символьные вычисления
Уже третью статью подряд мы с вами будем заниматься символьными вычислениями. Среда MathCAD, как вы сами уже имели возможность убедиться, имеет очень гибкие и мощные средства организации подобного рода вычислений. И вычисления эти в математике бывают важны и используются очень часто — именно поэтому мы с вами говорим о них столь подробно. Сегодня мы познакомимся с некоторыми новыми аспектами организации символьных вычислений в MathCAD'е, которые наверняка пригодятся вам при последующей работе с этой мощной математической средой.
Разложение на дроби
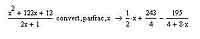 Мы уже говорили с вами о работе с дробями — точнее, о приведении суммы нескольких маленьких дробей к одной, но большой дроби. Теперь пришло время поговорить о процессе, диаметрально противоположном этому — о разложении одной дроби на сумму нескольких. Для решения этой задачи в MathCAD'е есть специальный оператор, который называется parfrac (от английского partial fraction — частные дроби). Использование этого оператора чрезвычайно простое, как, впрочем, и всех остальных операторов, которые можно найти на панели Symbolic. Достаточно, записав дробь, которую вы хотите разложить на сумму простых, затем выбрать на этой панели кнопку parfrac и указать имя переменной, для которой будет проводиться разложение. Когда вы добавите оператор parfrac, то перед ним автоматически добавится и оператор convert. Можете попробовать использовать их раздельно — уже на первой же дроби вы сможете собственноручно убедиться, что ничего ни хорошего, ни плохого из этого не выйдет — MathCAD просто не приемлет эти два оператора по отдельности.
Мы уже говорили с вами о работе с дробями — точнее, о приведении суммы нескольких маленьких дробей к одной, но большой дроби. Теперь пришло время поговорить о процессе, диаметрально противоположном этому — о разложении одной дроби на сумму нескольких. Для решения этой задачи в MathCAD'е есть специальный оператор, который называется parfrac (от английского partial fraction — частные дроби). Использование этого оператора чрезвычайно простое, как, впрочем, и всех остальных операторов, которые можно найти на панели Symbolic. Достаточно, записав дробь, которую вы хотите разложить на сумму простых, затем выбрать на этой панели кнопку parfrac и указать имя переменной, для которой будет проводиться разложение. Когда вы добавите оператор parfrac, то перед ним автоматически добавится и оператор convert. Можете попробовать использовать их раздельно — уже на первой же дроби вы сможете собственноручно убедиться, что ничего ни хорошего, ни плохого из этого не выйдет — MathCAD просто не приемлет эти два оператора по отдельности.
Тот же самый результат, не используя оператор parfrac, можно получить, выбрав в меню Symbolics пункт Variable, а в нем — Convert to Partial Fraction. В этом случае, правда, если что-то нужно будет изменить в исходном выражении, операцию придется повторить, поэтому лучше все же использовать оператор parfrac.
Оператор collect
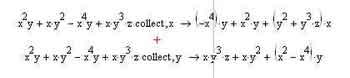 Мы уже говорили о работе со скобками в различных выражениях. Оператор collect является еще одним весьма и весьма полезным оператором, помогающим в работе со скобками — если конкретнее, то для вынесения из-за скобок общих множителей для полиномиальных выражений. Думаю, вы оцените все преимущества использования этого простого, но крайне эффективного оператора, если вам когда-нибудь будет нужно в реальных расчетах заниматься подобными вещами в практических целях. В общем-то, конечно, кто-то может сказать (и будет, пожалуй, прав), что поиск и вынесение за скобки общего множителя — не самая трудоемкая задача, а потому особой нужды в том, чтобы напрягать для ее решения MathCAD, пожалуй, что и нет. Однако на самом деле гибкость оператора collect позволяет проводить поиск даже самых замысловатых общих множителей, что вручную все-таки бывает не всегда удобно. Способ применения оператора collect действительно предельно прост. Мы, как обычно, записываем выражение, которое нужно преобразовать, а затем ищем на привычной уже нам панели Symbolic нужный нам оператор. После запятой в качестве параметра указывается имя переменной, которую мы будем выносить за скобки. Можно указывать не отдельную переменную, а какую-то функцию либо выражение — например, синус или логарифм. Правда, вынесение общих множителей реализовано довольно своеобразно — программа работает только с одной степенью переменной. То есть, если у вас будет запись вида x2+x, то она останется неизменной после применения оператора collect по переменной x.
Мы уже говорили о работе со скобками в различных выражениях. Оператор collect является еще одним весьма и весьма полезным оператором, помогающим в работе со скобками — если конкретнее, то для вынесения из-за скобок общих множителей для полиномиальных выражений. Думаю, вы оцените все преимущества использования этого простого, но крайне эффективного оператора, если вам когда-нибудь будет нужно в реальных расчетах заниматься подобными вещами в практических целях. В общем-то, конечно, кто-то может сказать (и будет, пожалуй, прав), что поиск и вынесение за скобки общего множителя — не самая трудоемкая задача, а потому особой нужды в том, чтобы напрягать для ее решения MathCAD, пожалуй, что и нет. Однако на самом деле гибкость оператора collect позволяет проводить поиск даже самых замысловатых общих множителей, что вручную все-таки бывает не всегда удобно. Способ применения оператора collect действительно предельно прост. Мы, как обычно, записываем выражение, которое нужно преобразовать, а затем ищем на привычной уже нам панели Symbolic нужный нам оператор. После запятой в качестве параметра указывается имя переменной, которую мы будем выносить за скобки. Можно указывать не отдельную переменную, а какую-то функцию либо выражение — например, синус или логарифм. Правда, вынесение общих множителей реализовано довольно своеобразно — программа работает только с одной степенью переменной. То есть, если у вас будет запись вида x2+x, то она останется неизменной после применения оператора collect по переменной x.
Коэффициенты многочленов
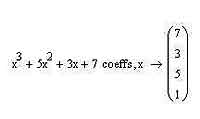 Иногда бывает полезно вынести коэффициенты многочлена в специальный столбец для того, чтобы потом ими оперировать. Конечно, для большинства распространенных задач полиномы не превышают третьей степени, и сделать это не так уж и сложно вручную. Однако зачем выполнять вручную то, что можно сделать одним оператором? Я думаю, вы согласитесь с тем, что это будет не слишком рациональным использованием времени, а потому имеет смысл применить оператор coeffs для того, чтобы получить готовый столбец коэффициентов. В общем-то, я думаю, вы уже догадались, как применять этот оператор. Нужно записать многочлен, а затем воспользоваться панелью Symbolic (еще раз напомню, что название оператора, который нужно в данном случае использовать, coeffs). Обращу ваше внимание на то, что столбец записывается снизу вверх от высших степеней многочлена к высшим. Также, конечно же, можно использовать именованные функции или другие выражения, которые возведены в различные степени.
Иногда бывает полезно вынести коэффициенты многочлена в специальный столбец для того, чтобы потом ими оперировать. Конечно, для большинства распространенных задач полиномы не превышают третьей степени, и сделать это не так уж и сложно вручную. Однако зачем выполнять вручную то, что можно сделать одним оператором? Я думаю, вы согласитесь с тем, что это будет не слишком рациональным использованием времени, а потому имеет смысл применить оператор coeffs для того, чтобы получить готовый столбец коэффициентов. В общем-то, я думаю, вы уже догадались, как применять этот оператор. Нужно записать многочлен, а затем воспользоваться панелью Symbolic (еще раз напомню, что название оператора, который нужно в данном случае использовать, coeffs). Обращу ваше внимание на то, что столбец записывается снизу вверх от высших степеней многочлена к высшим. Также, конечно же, можно использовать именованные функции или другие выражения, которые возведены в различные степени.
Ограничения на переменные в вычислениях
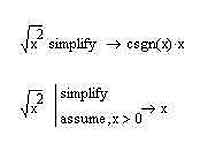 Иногда при использовании символьных вычислений есть необходимость выставить определенные ограничения в вычислениях, которые могут коренным образом упростить итоговое выражение. Действительно, весьма и весьма часто при решении прикладных задач по условиям этих самых задач на переменные накладываются определенные ограничения — например, очень часто переменные можно считать неотрицательными или даже строго больше нуля. Как рассказать MathCAD'у, что переменные ограничены определенным диапазоном значений? Естественно, для этого в этом мощном математическом пакете существует специальный оператор. И имя ему — assume. Оператор assume используется вместе с остальными операторами (особенно часто в сочетании с оператором simplify). Я уже рассказывал в прошлый раз о том, как изменяется внешний вид операторов символьных вычислений в MathCAD, а потому это не должно стать для вас сюрпризом.
Иногда при использовании символьных вычислений есть необходимость выставить определенные ограничения в вычислениях, которые могут коренным образом упростить итоговое выражение. Действительно, весьма и весьма часто при решении прикладных задач по условиям этих самых задач на переменные накладываются определенные ограничения — например, очень часто переменные можно считать неотрицательными или даже строго больше нуля. Как рассказать MathCAD'у, что переменные ограничены определенным диапазоном значений? Естественно, для этого в этом мощном математическом пакете существует специальный оператор. И имя ему — assume. Оператор assume используется вместе с остальными операторами (особенно часто в сочетании с оператором simplify). Я уже рассказывал в прошлый раз о том, как изменяется внешний вид операторов символьных вычислений в MathCAD, а потому это не должно стать для вас сюрпризом.
 В качестве ограничений, накладываемых на переменные, могут выступать не только минимальное и максимальное значения этой самой переменной. Для того, чтобы увидеть полный список всех возможных ограничений, нажмите на панели Symbolic кнопку Modifiers. Она, в отличие от большинства других кнопок на этой панели, не добавляет никаких новых операторов в рабочий лист MathCAD, а всего лишь показывает или прячет панель с модификаторами (modifiers) — эта панель как раз и пригодится нам для выставления различных ограничений на переменные при упрощении выражений и других символьных операциях.
В качестве ограничений, накладываемых на переменные, могут выступать не только минимальное и максимальное значения этой самой переменной. Для того, чтобы увидеть полный список всех возможных ограничений, нажмите на панели Symbolic кнопку Modifiers. Она, в отличие от большинства других кнопок на этой панели, не добавляет никаких новых операторов в рабочий лист MathCAD, а всего лишь показывает или прячет панель с модификаторами (modifiers) — эта панель как раз и пригодится нам для выставления различных ограничений на переменные при упрощении выражений и других символьных операциях.
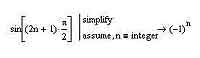 Как видите, модификаторов в панели не так уж много, а потому мы поговорим о каждом из них. Первый — это, как вы можете заметить, уже довольно неплохо знакомый нам с вами assume. Не буду повторяться — о его использовании я рассказывал всего парой абзацев выше. Второй по счету модификатор — это real. Поскольку MathCAD может оперировать и комплексными числами (об этой полезной возможности мы с вами еще обязательно поговорим), то местами в подобных вычислениях полезно наложить на переменную ограничение и определить ее как действительную. RealRange — третий по счету модификатор на панели Modifiers — это двустороннее ограничение на действительную переменную на определенном отрезке (то есть, обратите внимание, концы этого отрезка также попадут в область значений нашей переменной). Четвертый модификатор имеет название trig, и он обозначает переменную как тригонометрическую величину. Этот модификатор используется по сравнению с остальными совсем не часто, поскольку при работе с тригонометрическими функциями все же предпочтительнее использовать их общепринятые обозначения, которые, будучи совсем не длинными, сильно упрощают чтение проекта и уменьшают вероятность в нем запутаться. Последний модификатор, который можно найти на панели, — это модификатор integer. Он используется для задания целочисленных переменных. Используются модификаторы для указания выражений в операторе assume. То есть, например, если мы хотим указать при вычислении какого-либо символьного выражения, что переменная n у нас будет целочисленной, то мы должны записать после оператора assume следующее: n = integer. Совершенно аналогично и для всех остальных модификаторов, которые были описаны выше.
Как видите, модификаторов в панели не так уж много, а потому мы поговорим о каждом из них. Первый — это, как вы можете заметить, уже довольно неплохо знакомый нам с вами assume. Не буду повторяться — о его использовании я рассказывал всего парой абзацев выше. Второй по счету модификатор — это real. Поскольку MathCAD может оперировать и комплексными числами (об этой полезной возможности мы с вами еще обязательно поговорим), то местами в подобных вычислениях полезно наложить на переменную ограничение и определить ее как действительную. RealRange — третий по счету модификатор на панели Modifiers — это двустороннее ограничение на действительную переменную на определенном отрезке (то есть, обратите внимание, концы этого отрезка также попадут в область значений нашей переменной). Четвертый модификатор имеет название trig, и он обозначает переменную как тригонометрическую величину. Этот модификатор используется по сравнению с остальными совсем не часто, поскольку при работе с тригонометрическими функциями все же предпочтительнее использовать их общепринятые обозначения, которые, будучи совсем не длинными, сильно упрощают чтение проекта и уменьшают вероятность в нем запутаться. Последний модификатор, который можно найти на панели, — это модификатор integer. Он используется для задания целочисленных переменных. Используются модификаторы для указания выражений в операторе assume. То есть, например, если мы хотим указать при вычислении какого-либо символьного выражения, что переменная n у нас будет целочисленной, то мы должны записать после оператора assume следующее: n = integer. Совершенно аналогично и для всех остальных модификаторов, которые были описаны выше.
 Кстати, при преобразовании выражений наподобие того, что приведено на иллюстрации чуть выше, совершенно не обязательно использовать assume вместе с simplify. Если вы уберете оператор simplify, то сможете сами убедиться в том, что без него выражение будет вычислено ничуть не хуже. Правда, если пойти дальше и убрать еще и assume, оставив при этом n = integer, то MathCAD выдаст ошибку с сообщением о неверном синтаксисе команды.
Кстати, при преобразовании выражений наподобие того, что приведено на иллюстрации чуть выше, совершенно не обязательно использовать assume вместе с simplify. Если вы уберете оператор simplify, то сможете сами убедиться в том, что без него выражение будет вычислено ничуть не хуже. Правда, если пойти дальше и убрать еще и assume, оставив при этом n = integer, то MathCAD выдаст ошибку с сообщением о неверном синтаксисе команды.
Оператор float
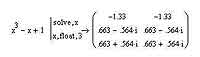 Напоследок мы с вами поговорим о еще одном весьма полезном операторе, который, будучи оператором символьных вычислений, используется для получения конкретного результата в виде числа. Оператор float используется тогда, когда нужно получить результат символьных вычислений не в виде формулы, а в виде числа. Вполне понятно, что применять его можно исключительно в тех случаях, когда все числа в выражении заданы не в общем виде (т.е. не какими-то именованными константами), а конкретными значениями. В противном случае MathCAD ошибки не выдаст, однако использование оператора float будет напрочь лишено смысла. Для того, чтобы проиллюстрировать использование этого оператора, обратимся к примеру кубического уравнения, который рассматривался в предыдущей части нашей серии статей по MathCAD'у. Решения кубических уравнений в виде формул занимают очень много места и отличаются громоздкостью, а потому их целесообразно упрощать с помощью оператора float. Можете сравнить формульные результаты, полученные нами в прошлый раз, с тем, как они записываются с помощью этого оператора: разница, как говорится, налицо.
Напоследок мы с вами поговорим о еще одном весьма полезном операторе, который, будучи оператором символьных вычислений, используется для получения конкретного результата в виде числа. Оператор float используется тогда, когда нужно получить результат символьных вычислений не в виде формулы, а в виде числа. Вполне понятно, что применять его можно исключительно в тех случаях, когда все числа в выражении заданы не в общем виде (т.е. не какими-то именованными константами), а конкретными значениями. В противном случае MathCAD ошибки не выдаст, однако использование оператора float будет напрочь лишено смысла. Для того, чтобы проиллюстрировать использование этого оператора, обратимся к примеру кубического уравнения, который рассматривался в предыдущей части нашей серии статей по MathCAD'у. Решения кубических уравнений в виде формул занимают очень много места и отличаются громоздкостью, а потому их целесообразно упрощать с помощью оператора float. Можете сравнить формульные результаты, полученные нами в прошлый раз, с тем, как они записываются с помощью этого оператора: разница, как говорится, налицо.
Думаю, синтаксис использования этого оператора вполне понятен из примера: в качестве первого параметра (до оператора) — выражение, которое нужно вычислить (в приведенном примере его, конечно, лучше опускать, потому что иначе это приводит, как показано на иллюстрации, к дублированию результата), а в качестве второго (после оператора) — точность, т.е. количество значимых цифр после запятой, остающихся после вычислений. Что ж, пока что, я так думаю, хватит на этот раз — нехорошо было бы перегружать вас, уважаемые читатели, информацией, тем более, что тема символьных вычислений в MathCAD'е явно не относится к тем, которые можно обсуждать практически бесконечно за чашкой чая или кофе. Я думаю, что те операторы, которые мы сегодня рассмотрели, наверняка пригодятся вам в повседневных буднях вычислений в MathCAD'е, и вы еще не раз будете добрым словом поминать разработчиков этого всесторонне замечательного математического пакета, предусмотревших для вас все эти возможности.
SF, spaceflyer@tut.by
Разложение на дроби
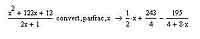
Тот же самый результат, не используя оператор parfrac, можно получить, выбрав в меню Symbolics пункт Variable, а в нем — Convert to Partial Fraction. В этом случае, правда, если что-то нужно будет изменить в исходном выражении, операцию придется повторить, поэтому лучше все же использовать оператор parfrac.
Оператор collect
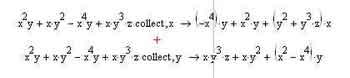
Коэффициенты многочленов
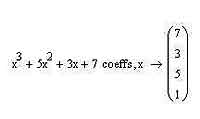
Ограничения на переменные в вычислениях
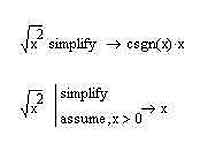

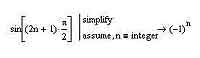

Оператор float
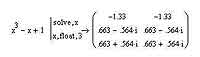
Думаю, синтаксис использования этого оператора вполне понятен из примера: в качестве первого параметра (до оператора) — выражение, которое нужно вычислить (в приведенном примере его, конечно, лучше опускать, потому что иначе это приводит, как показано на иллюстрации, к дублированию результата), а в качестве второго (после оператора) — точность, т.е. количество значимых цифр после запятой, остающихся после вычислений. Что ж, пока что, я так думаю, хватит на этот раз — нехорошо было бы перегружать вас, уважаемые читатели, информацией, тем более, что тема символьных вычислений в MathCAD'е явно не относится к тем, которые можно обсуждать практически бесконечно за чашкой чая или кофе. Я думаю, что те операторы, которые мы сегодня рассмотрели, наверняка пригодятся вам в повседневных буднях вычислений в MathCAD'е, и вы еще не раз будете добрым словом поминать разработчиков этого всесторонне замечательного математического пакета, предусмотревших для вас все эти возможности.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 30 за 2008 год в рубрике soft


