MathCAD — это просто! Часть 15. Знакомство с символьными вычислениями
Мы с вами уже неоднократно употребляли такой термин, как символьный процессор MathCAD. Даже говорили о том, что некоторые вещи (скажем, те же определенные интегралы, которые мы с вами совсем недавно весьма и весьма подробно обсуждали) можно вычислять в MathCAD двумя принципиально отличающимися друг от друга путями: символьным и численным. Однако подробного и обстоятельного разговора о символьных вычислениях в MathCAD у нас еще до сих пор не было. Тем не менее, поскольку символьные вычисления являются очень важным аспектом использования на практике этой математической среды, то и поговорить о них мы, как бы то ни было, в любом случае рано или поздно должны. И лучше это не откладывать на потом, а заняться таким полезным делом, как символьные вычисления, прямо сейчас. Конечно, в одной статье, даже довольно большой, невозможно будет уместить рассказ не то что обо всех возможностях символьного процессора MathCAD'а, но даже хотя бы о самой существенной их части. Именно поэтому эта статья и называется "Знакомство с символьными вычислениями".
Символьный процессор
 Символьные вычисления выполняются встроенным в MathCAD символьным процессором, который уже упоминался неоднократно в предыдущих статьях. Стоит отметить, что символьный процессор — это та часть MathCAD'а, которая написана не самой компанией MathSoft, создавшей этот замечательный математический пакет, а фирмой Waterloo Maple Software. Об этом свидетельствует окно About, которое можно вызвать в меню Help. Waterloo Maple Software — компания, разрабатывающая другой известный математический пакет, который называется Maple. Однако это вовсе не означает, что возможности символьного вычисления в MathCAD полностью соответствуют его возможностям в Maple. Дело в том, что в MathCAD используется несколько урезанная версия символьного процессора Maple. Однако это не значит, что символьные вычисления в MathCAD реализованы хуже — вы убедитесь сами, что с помощью встроенного в MathCAD символьного процессора можно делать очень много всяческих полезных вещей.
Символьные вычисления выполняются встроенным в MathCAD символьным процессором, который уже упоминался неоднократно в предыдущих статьях. Стоит отметить, что символьный процессор — это та часть MathCAD'а, которая написана не самой компанией MathSoft, создавшей этот замечательный математический пакет, а фирмой Waterloo Maple Software. Об этом свидетельствует окно About, которое можно вызвать в меню Help. Waterloo Maple Software — компания, разрабатывающая другой известный математический пакет, который называется Maple. Однако это вовсе не означает, что возможности символьного вычисления в MathCAD полностью соответствуют его возможностям в Maple. Дело в том, что в MathCAD используется несколько урезанная версия символьного процессора Maple. Однако это не значит, что символьные вычисления в MathCAD реализованы хуже — вы убедитесь сами, что с помощью встроенного в MathCAD символьного процессора можно делать очень много всяческих полезных вещей.
Итак, давайте определимся: для какого рода вычислений используется символьный процессор? С этим, к счастью, все просто. Если вы хотите получить не число в результате преобразования какого-либо выражения либо решения уравнения, а аналитическую формулу, то это и называется символьными вычислениями. Именно таким родом вычислений и занимается символьный процессор. Стоит еще заметить, что, к сожалению, далеко не всегда символьный процессор способен выдавать результат именно в том виде, в каком его ожидаете увидеть вы. И даже более того: сам по себе результат в каком бы то ни было виде тоже далеко не всегда может быть найден. Дело здесь, в общем-то, не столько в каких-то внутренних дефектах или ограничениях символьного процессора MathCAD'а, сколько в том, что компьютерам, вообще говоря, не слишком свойственно креативное мышление, которое и является залогом успешного решения любой математической задачи. Очень часто компьютер может элементарно "не догадываться" о тех или иных приемах, которые представляются элементарными знакомому с математикой человеку, и глупо на него за это обижаться. Лучше заранее быть готовым к ограниченности символьного процессора и иметь в запасе бумажку с ручкой, чтобы самостоятельно преобразовать выражение к тому виду, который уже будет понятен символьному процессору, и с которым тот уже будет в состоянии разобраться. Символьные алгоритмы, в отличие от численных, принципиально довольно сложны, а потому мы не будем рассматривать подноготную символьного процессора, как это делали с численными методами расчета определенных интегралов.
Упрощение выражений
 Упрощение аналитических выражений — это, пожалуй, одна из самых частых задач, с которыми сталкивается любой человек, работающий с формулами. Чем проще выражение, тем проще вычислять какие-либо конкретные значения тех или иных величин с его использованием, и тем проще анализировать его, что немаловажно, когда перед нами стоит задача анализа не просто абстрактной математической формулы, а некой физической, экономической или иной статистической закономерности, которая скрывается за ней. Потому нет ничего удивительного в том, что упрощение выражений является одной из самых важных способностей символьного процессора, встроенного в математическую среду MathCAD. В общем-то, поскольку сам MathCAD часто и сам выдает результаты других видов символьных преобразований в несколько, мягко говоря, неудобном для нормального человеческого восприятия виде, то упрощение выражений может использоваться в проектах MathCAD особенно часто.
Упрощение аналитических выражений — это, пожалуй, одна из самых частых задач, с которыми сталкивается любой человек, работающий с формулами. Чем проще выражение, тем проще вычислять какие-либо конкретные значения тех или иных величин с его использованием, и тем проще анализировать его, что немаловажно, когда перед нами стоит задача анализа не просто абстрактной математической формулы, а некой физической, экономической или иной статистической закономерности, которая скрывается за ней. Потому нет ничего удивительного в том, что упрощение выражений является одной из самых важных способностей символьного процессора, встроенного в математическую среду MathCAD. В общем-то, поскольку сам MathCAD часто и сам выдает результаты других видов символьных преобразований в несколько, мягко говоря, неудобном для нормального человеческого восприятия виде, то упрощение выражений может использоваться в проектах MathCAD особенно часто.
Для упрощения выражений используется оператор simplify. Его можно найти на панели Symbolic, которая отличается от других рассмотренных нами панелей главного окна MathCAD тем, что на ней используются не пиктограммы (так называемые "иконки"), а полные варианты написания операторов (за исключением нескольких операторов для работы с матрицами, о которых мы с вами уже говорили, когда разбирались с матричными вычислениями в среде MathCAD).
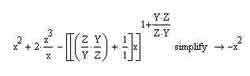 Использовать оператор упрощения выражений в MathCAD чрезвычайно просто. Достаточно записать выражение, которое вам нужно упростить, нажать на панели символьных вычислений кнопку, отвечающую за вставку оператора символьного упрощения выражения, и, в общем-то, на этом ваша работа по упрощению выражения, если вам повезет, закончится — дальше за вас все будет делать MathCAD. Если же не повезет, то, как я уже говорил выше, запасной вариант — это ручка, бумага и справочник с формулами.
Использовать оператор упрощения выражений в MathCAD чрезвычайно просто. Достаточно записать выражение, которое вам нужно упростить, нажать на панели символьных вычислений кнопку, отвечающую за вставку оператора символьного упрощения выражения, и, в общем-то, на этом ваша работа по упрощению выражения, если вам повезет, закончится — дальше за вас все будет делать MathCAD. Если же не повезет, то, как я уже говорил выше, запасной вариант — это ручка, бумага и справочник с формулами.
Разложение выражений на множители
Иногда, впрочем, может быть полезен (и мало того, что полезен, но и вовсе необходим для успешного решения задачи) процесс, целиком и полностью обратный упрощению выражений. Процесс этот, конечно, называется не усложнением выражений, а их разложением. Разложение может быть разным, потому что термин этот в математике, надо сказать, весьма и весьма емкий. Можно раскладывать выражение на слагаемые (например, дробь — на сумму простых дробей), можно раскладывать функцию в ряд Фурье или Тейлора, а можно раскладывать многочлен на произведения… В общем, раскладывать нам придется много всего разного. Постараемся поговорить обо всех аспектах этого вида символьных преобразований. Для начала рассмотрим такой процесс, при котором выражение раскладывается на множители — он носит название факторизации и используется самым что ни на есть широким образом в современной криптографии. Для факторизации используется оператор factor, найти который, как вы, наверное, уже догадались, можно на панели Symbolic (там же, где и все остальные операторы символьных вычислений). В случае большинства выражений пользоваться оператором factor ничуть не сложнее, чем оператором simplify. То есть достаточно записать выражение и сам оператор, после чего MathCAD, если это вообще возможно, разложит записанное выражение на множители.
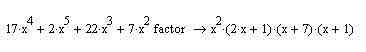 Однако есть случаи, когда такой простой вид оператора factor может оказаться недостаточным. Наверное, когда вы вводили этот оператор в рабочую область MathCAD, то уже успели обратить внимание на то, что по умолчанию программа предлагает ввести после него еще один дополнительный параметр. Что это за параметр, и что именно он делает? Предложу вам сначала взглянуть на иллюстрацию, на которой оператор факторизации используется именно с этим параметром и без него, и сравнить, чем отличаются результаты. После я отдельно прокомментирую его использование, и вы сможете сравнить ваши выводы с правильным ответом. Думаю, он вас удивит.
Однако есть случаи, когда такой простой вид оператора factor может оказаться недостаточным. Наверное, когда вы вводили этот оператор в рабочую область MathCAD, то уже успели обратить внимание на то, что по умолчанию программа предлагает ввести после него еще один дополнительный параметр. Что это за параметр, и что именно он делает? Предложу вам сначала взглянуть на иллюстрацию, на которой оператор факторизации используется именно с этим параметром и без него, и сравнить, чем отличаются результаты. После я отдельно прокомментирую его использование, и вы сможете сравнить ваши выводы с правильным ответом. Думаю, он вас удивит.
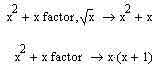 В справочной системе MathCAD говорится, что параметр (или, говоря более точно терминами самого MathCAD'а, второй маркер ввода) требуется для разложения корней. Т.е. если мы хотим сказать MathCAD, чтобы он раскладывал все до определенной дробной степени переменных, то должны, если верить справке, указывать наши пожелания именно в этом параметре. К сожалению, в данном случае справочная система MathCAD'а несколько подмачивает свою репутацию, поскольку вводит нас в заблуждение. Дело в том, что, как вы можете увидеть из иллюстрации, при попытке указать подобные вещи алгоритму факторизации тот вообще перестает работать. Если вы попробуете перебирать различные варианты параметров или обратитесь к примерам MathCAD'а (т.н. Quicksheets), то увидите, что все, что приведено в Quicksheets, прекрасно работает и без использования второго параметра. Поэтому, если вы подумали, что он нужен для того, чтобы факторизация перестала работать, то поздравляю, ваш ответ верен — на сегодняшний день все обстоит именно так. Поэтому, работая с оператором factor, сразу удаляйте запятую и пустое место для параметра после нее.
В справочной системе MathCAD говорится, что параметр (или, говоря более точно терминами самого MathCAD'а, второй маркер ввода) требуется для разложения корней. Т.е. если мы хотим сказать MathCAD, чтобы он раскладывал все до определенной дробной степени переменных, то должны, если верить справке, указывать наши пожелания именно в этом параметре. К сожалению, в данном случае справочная система MathCAD'а несколько подмачивает свою репутацию, поскольку вводит нас в заблуждение. Дело в том, что, как вы можете увидеть из иллюстрации, при попытке указать подобные вещи алгоритму факторизации тот вообще перестает работать. Если вы попробуете перебирать различные варианты параметров или обратитесь к примерам MathCAD'а (т.н. Quicksheets), то увидите, что все, что приведено в Quicksheets, прекрасно работает и без использования второго параметра. Поэтому, если вы подумали, что он нужен для того, чтобы факторизация перестала работать, то поздравляю, ваш ответ верен — на сегодняшний день все обстоит именно так. Поэтому, работая с оператором factor, сразу удаляйте запятую и пустое место для параметра после нее.
Ну, а если вдруг найдете какой-нибудь экзотический случай, в котором эта запятая полезна, то, пожалуйста, не поленитесь написать мне о нем. Вполне возможно, что подобная странность оператора factor связана с происхождением MathCAD'овского символьного процессора. Дополнительный параметр мог использоваться в Maple, а разработчики MathCAD'а просто механически перенесли его описание в документацию, забыв проверить, каким образом он работает в их программе. Однако, конечно, это все домыслы, и как все было на самом деле, знают только работники MathSoft. Что ж, успели мы с вами рассмотреть не так уж много, однако упрощение выражений и их факторизация играют весьма и весьма существенную роль в символьных вычислениях, а потому лучше разобраться с ними как можно полнее и внимательнее. Конечно, точно так же, как и формульные выражения, вы можете преобразовывать и числа (факторизуются, конечно, только целые числа, не являющиеся простыми). И, несмотря на некоторые странности в своей работе, символьный процессор — действительно очень полезная часть MathCAD.
SF, spaceflyer@tut.by
Символьный процессор

Итак, давайте определимся: для какого рода вычислений используется символьный процессор? С этим, к счастью, все просто. Если вы хотите получить не число в результате преобразования какого-либо выражения либо решения уравнения, а аналитическую формулу, то это и называется символьными вычислениями. Именно таким родом вычислений и занимается символьный процессор. Стоит еще заметить, что, к сожалению, далеко не всегда символьный процессор способен выдавать результат именно в том виде, в каком его ожидаете увидеть вы. И даже более того: сам по себе результат в каком бы то ни было виде тоже далеко не всегда может быть найден. Дело здесь, в общем-то, не столько в каких-то внутренних дефектах или ограничениях символьного процессора MathCAD'а, сколько в том, что компьютерам, вообще говоря, не слишком свойственно креативное мышление, которое и является залогом успешного решения любой математической задачи. Очень часто компьютер может элементарно "не догадываться" о тех или иных приемах, которые представляются элементарными знакомому с математикой человеку, и глупо на него за это обижаться. Лучше заранее быть готовым к ограниченности символьного процессора и иметь в запасе бумажку с ручкой, чтобы самостоятельно преобразовать выражение к тому виду, который уже будет понятен символьному процессору, и с которым тот уже будет в состоянии разобраться. Символьные алгоритмы, в отличие от численных, принципиально довольно сложны, а потому мы не будем рассматривать подноготную символьного процессора, как это делали с численными методами расчета определенных интегралов.
Упрощение выражений

Для упрощения выражений используется оператор simplify. Его можно найти на панели Symbolic, которая отличается от других рассмотренных нами панелей главного окна MathCAD тем, что на ней используются не пиктограммы (так называемые "иконки"), а полные варианты написания операторов (за исключением нескольких операторов для работы с матрицами, о которых мы с вами уже говорили, когда разбирались с матричными вычислениями в среде MathCAD).
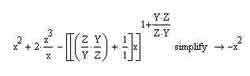
Разложение выражений на множители
Иногда, впрочем, может быть полезен (и мало того, что полезен, но и вовсе необходим для успешного решения задачи) процесс, целиком и полностью обратный упрощению выражений. Процесс этот, конечно, называется не усложнением выражений, а их разложением. Разложение может быть разным, потому что термин этот в математике, надо сказать, весьма и весьма емкий. Можно раскладывать выражение на слагаемые (например, дробь — на сумму простых дробей), можно раскладывать функцию в ряд Фурье или Тейлора, а можно раскладывать многочлен на произведения… В общем, раскладывать нам придется много всего разного. Постараемся поговорить обо всех аспектах этого вида символьных преобразований. Для начала рассмотрим такой процесс, при котором выражение раскладывается на множители — он носит название факторизации и используется самым что ни на есть широким образом в современной криптографии. Для факторизации используется оператор factor, найти который, как вы, наверное, уже догадались, можно на панели Symbolic (там же, где и все остальные операторы символьных вычислений). В случае большинства выражений пользоваться оператором factor ничуть не сложнее, чем оператором simplify. То есть достаточно записать выражение и сам оператор, после чего MathCAD, если это вообще возможно, разложит записанное выражение на множители.
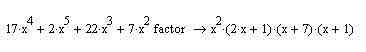
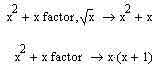
Ну, а если вдруг найдете какой-нибудь экзотический случай, в котором эта запятая полезна, то, пожалуйста, не поленитесь написать мне о нем. Вполне возможно, что подобная странность оператора factor связана с происхождением MathCAD'овского символьного процессора. Дополнительный параметр мог использоваться в Maple, а разработчики MathCAD'а просто механически перенесли его описание в документацию, забыв проверить, каким образом он работает в их программе. Однако, конечно, это все домыслы, и как все было на самом деле, знают только работники MathSoft. Что ж, успели мы с вами рассмотреть не так уж много, однако упрощение выражений и их факторизация играют весьма и весьма существенную роль в символьных вычислениях, а потому лучше разобраться с ними как можно полнее и внимательнее. Конечно, точно так же, как и формульные выражения, вы можете преобразовывать и числа (факторизуются, конечно, только целые числа, не являющиеся простыми). И, несмотря на некоторые странности в своей работе, символьный процессор — действительно очень полезная часть MathCAD.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 28 за 2008 год в рубрике soft


