MathCAD — это просто! Часть 14. Глубины интегрирования и другие интересные вещи
Изучая MathCAD с помощью серии статей "MathCAD — это просто", мы с вами добрались до такого непростого вопроса, как интегрирование функций. Поговорив с вами о таких полезных вещах, как полные и частные производные, мы, если вы помните, перебрались сначала к неопределенным, а потом — и к определенным интегралам. Говоря об определенных интегралах, мы выяснили, что вычислять их можно двумя (как это обычно и водится в MathCAD'е) способами: аналитически, препоручая наш интеграл заботам символьного процессора, или численно. Второй способ вычисления интегралов позволяет вычислять даже так называемые неберущиеся интегралы — то есть такие, которые не могут быть проинтегрированы в виде неопределенного интеграла таким образом, чтобы результат мог быть получен в виде композиции элементарных функций. Однако здесь, что называется, зарыта собака, способная напрочь испортить все то хорошее, что мы имеем, применяя численные методы интегрирования. Вот об этой злокозненной собаке, а также о некоторых других интересных и полезных вещах мы с вами прямо сейчас и станем говорить.
Несобственные интегралы
Перед тем, как углубляться во внутренние процессы вычисления интегралов численными методами, стоит немного поговорить о вычислении несобственных интегралов. Тема эта, впрочем, совсем не сложная, а потому и говорить о них мы с вами будем совсем чуть-чуть.
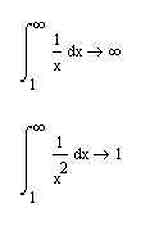 Напомню, что несобственным называется определенный интеграл, у которого хотя бы одна из границ интегрирования равняется бесконечности. Несобственные интегралы могут быть сходящимися или расходящимися, то есть не равными или равными бесконечности. Например, значения несобственного интеграла от нуля до плюс бесконечности для любой возрастающей функции всегда будет бесконечным. Для убывающих функций, как правило, подобные интегралы сходятся, хотя это тоже не всегда так — для этого функция, помимо убывания, должна удовлетворять еще ряду критериев, найти которые можно в любом учебнике по математическому анализу. Что касается вычисления несобственных интегралов в среде MathCAD, то здесь, в общем-то, особой разницы между несобственными и всеми остальными определенными интегралами нет. Для вычисления несобственного интеграла достаточно установить в качестве граничного значения бесконечность (напомню: для этого достаточно воспользоваться соответствующей кнопкой на панели Calculus), и MathCAD посчитает вам несобственный интеграл.
Напомню, что несобственным называется определенный интеграл, у которого хотя бы одна из границ интегрирования равняется бесконечности. Несобственные интегралы могут быть сходящимися или расходящимися, то есть не равными или равными бесконечности. Например, значения несобственного интеграла от нуля до плюс бесконечности для любой возрастающей функции всегда будет бесконечным. Для убывающих функций, как правило, подобные интегралы сходятся, хотя это тоже не всегда так — для этого функция, помимо убывания, должна удовлетворять еще ряду критериев, найти которые можно в любом учебнике по математическому анализу. Что касается вычисления несобственных интегралов в среде MathCAD, то здесь, в общем-то, особой разницы между несобственными и всеми остальными определенными интегралами нет. Для вычисления несобственного интеграла достаточно установить в качестве граничного значения бесконечность (напомню: для этого достаточно воспользоваться соответствующей кнопкой на панели Calculus), и MathCAD посчитает вам несобственный интеграл.
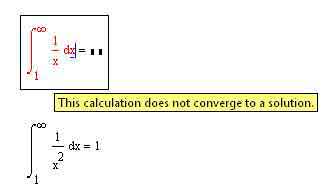 Как и в случае с остальными определенными интегралами, лучше по возможности считать их с помощью символьного процессора, то есть аналитически. Если это по какой-либо причине невозможно, то тогда уже придется обратиться к численному расчету. Однако здесь многих может ожидать довольно неприятная неожиданность: несходящиеся интегралы при численном интегрировании MathCAD считает чем-то вроде природной аномалии. Потому, если у вас при численном вычислении несобственного интеграла MathCAD выдает ошибку (см. соответствующую иллюстрацию к статье), то знайте, что вы, скорее всего, все сделали правильно, просто значение этого интеграла равно бесконечности.
Как и в случае с остальными определенными интегралами, лучше по возможности считать их с помощью символьного процессора, то есть аналитически. Если это по какой-либо причине невозможно, то тогда уже придется обратиться к численному расчету. Однако здесь многих может ожидать довольно неприятная неожиданность: несходящиеся интегралы при численном интегрировании MathCAD считает чем-то вроде природной аномалии. Потому, если у вас при численном вычислении несобственного интеграла MathCAD выдает ошибку (см. соответствующую иллюстрацию к статье), то знайте, что вы, скорее всего, все сделали правильно, просто значение этого интеграла равно бесконечности.
Кухня численного интегрирования
В общем и целом вычисление интегралов численными методами — это фактически использование математического определения (простите за тавтологию) определенного интеграла. Что это значит? Давайте попробуем вспомнить, как трактуются определенные интегралы с точки зрения математического анализа.
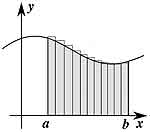 Для иллюстрации понятия определенного интеграла чаще всего прибегают к прикладной задаче, легко решаемой с помощью интегрирования — определению площади фигуры под кривой, заданной какой-либо функцией. Для вычисления этой площади используется следующий подход: участок оси OX от a до b (см. иллюстрацию) разбивается на несколько мелких участков, для каждого из которых рассчитывается площадь прямоугольника, ограниченного прямыми, проведенными до пересечения с графиком функции, который ограничивает фигуру. Если мы просуммируем потом площади этих прямоугольников, то как раз и получится величина, приблизительно равная площади фигуры под графиком. Для того, чтобы от приблизительного равенства перейти к точному, надо устремить к нулю длину каждого из отрезков, на которые мы разбиваем участок оси OX от a до b, и тогда определенный интеграл будет равен пределу суммы площадей получившихся в результате прямоугольников. Такой определенный интеграл математики называют определенным интегралом в римановом смысле, или интегралом в смысле Римана.
Для иллюстрации понятия определенного интеграла чаще всего прибегают к прикладной задаче, легко решаемой с помощью интегрирования — определению площади фигуры под кривой, заданной какой-либо функцией. Для вычисления этой площади используется следующий подход: участок оси OX от a до b (см. иллюстрацию) разбивается на несколько мелких участков, для каждого из которых рассчитывается площадь прямоугольника, ограниченного прямыми, проведенными до пересечения с графиком функции, который ограничивает фигуру. Если мы просуммируем потом площади этих прямоугольников, то как раз и получится величина, приблизительно равная площади фигуры под графиком. Для того, чтобы от приблизительного равенства перейти к точному, надо устремить к нулю длину каждого из отрезков, на которые мы разбиваем участок оси OX от a до b, и тогда определенный интеграл будет равен пределу суммы площадей получившихся в результате прямоугольников. Такой определенный интеграл математики называют определенным интегралом в римановом смысле, или интегралом в смысле Римана.
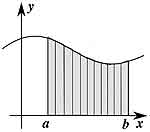 Фактически большая часть численных методов вычисления определенных интегралов использует как раз риманово определение. Конечно, отрезки берутся не бесконечно малыми, но, тем не менее, довольно мелкими. Однако именно конечные размеры отрезков разбиения являются, по существу, основным источником ошибок и погрешностей при численном интегрировании. С ними (погрешностями) борются. Конечно, здесь тоже есть вариации. Например, если вы внимательно посмотрите на иллюстрацию к определению интеграла в римановом смысле, то легко сможете заметить, что использование прямоугольников в качестве базовых фигур для расчета площади — далеко не лучший из возможных вариантов. Если мы воспользуемся трапециями, верхние стороны которых будут соединять пересечения прямых, проведенных из концов отрезков разбиения, с графиком функции, то итоговое значение площади фигуры получится куда более точным, чем в том случае, когда мы использовали прямоугольники. Еще большей точности можно добиться, используя вместо прямых линий графики полиномов, однако это уже может существенно замедлить процесс вычисления значения определенного интеграла.
Фактически большая часть численных методов вычисления определенных интегралов использует как раз риманово определение. Конечно, отрезки берутся не бесконечно малыми, но, тем не менее, довольно мелкими. Однако именно конечные размеры отрезков разбиения являются, по существу, основным источником ошибок и погрешностей при численном интегрировании. С ними (погрешностями) борются. Конечно, здесь тоже есть вариации. Например, если вы внимательно посмотрите на иллюстрацию к определению интеграла в римановом смысле, то легко сможете заметить, что использование прямоугольников в качестве базовых фигур для расчета площади — далеко не лучший из возможных вариантов. Если мы воспользуемся трапециями, верхние стороны которых будут соединять пересечения прямых, проведенных из концов отрезков разбиения, с графиком функции, то итоговое значение площади фигуры получится куда более точным, чем в том случае, когда мы использовали прямоугольники. Еще большей точности можно добиться, используя вместо прямых линий графики полиномов, однако это уже может существенно замедлить процесс вычисления значения определенного интеграла.
В MathCAD основным алгоритмом, используемым при численном интегрировании, является алгоритм, основанный как раз на использовании трапеций — этот метод вычисления определенных интегралов называется методом Ромберга. Есть в MathCAD и другой численный метод, используемый для вычисления интегралов от быстро изменяющихся функций — его разработчики этого математического пакета называли адаптивным. Его отличие от метода Ромберга заключается в том, что шаг разбиения интервала, на котором производится интегрирование, изменяется в соответствии со скоростью изменения значения самой функции, что позволяет дополнительно минимизировать погрешность. Еще одно преимущество этого метода интегрирования заключается в том, что мы можем с его помощью хорошо управляться с разрывами первого рода, которые при использовании метода Ромберга часто вообще приводят к тому, что функцию становится невозможным проинтегрировать численно. Напомню, что разрывом первого рода называется точка, для которой правосторонний и левосторонний пределы функции не равны друг другу, но при этом конечны. Если же хотя бы один из пределов бесконечен, то тогда точка называется разрывом второго рода.
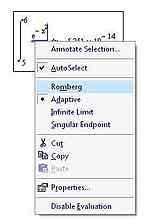 MathCAD по умолчанию использует именно адаптивный метод вычисления определенных интегралов, поскольку он, как я уже говорил, более гибок в отношении различных типов функций. Впрочем, вы можете воспользоваться и методом Ромберга, если в этом возникнет необходимость. Для этого кликните правой кнопкой мыши по тому интегралу, метод вычисления которого вы желаете изменить, и выберите в появившемся контекстном меню пункт Romberg. Впрочем, наилучшим вариантом все же будет используемый по умолчанию Auto Select, поскольку тогда сам MathCAD определит метод, согласно которому будет вычисляться данный интеграл. А метод он подбирает обычно правильно, то есть, если вы предоставите выбирать все самому MathCAD'у, то это будет, пожалуй, самым удачным решением.
MathCAD по умолчанию использует именно адаптивный метод вычисления определенных интегралов, поскольку он, как я уже говорил, более гибок в отношении различных типов функций. Впрочем, вы можете воспользоваться и методом Ромберга, если в этом возникнет необходимость. Для этого кликните правой кнопкой мыши по тому интегралу, метод вычисления которого вы желаете изменить, и выберите в появившемся контекстном меню пункт Romberg. Впрочем, наилучшим вариантом все же будет используемый по умолчанию Auto Select, поскольку тогда сам MathCAD определит метод, согласно которому будет вычисляться данный интеграл. А метод он подбирает обычно правильно, то есть, если вы предоставите выбирать все самому MathCAD'у, то это будет, пожалуй, самым удачным решением.
Вы наверняка заметили, что, кроме метода Ромберга и адаптивного метода вычисления интегралов, в контекстном меню можно выбрать еще два других метода — Infinite Limit и Singular Endpoint. Эти методы используются для вычисления несобственных интегралов. Метод Singular Endpoint — это еще одна разновидность метода Ромберга, специально предназначенная для несобственных интегралов, а про Infinite Limit разработчики MathCAD распространяться по каким-то одним им известным причинам не захотели.
Интегралы с параметрами
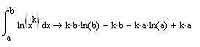 Напоследок еще совсем чуть-чуть поговорим про интегралы с параметрами. Почему чуть-чуть? Да потому, что работать с ними в MathCAD'е ничуть не сложнее, чем со всеми остальными типами интегралов, с которыми мы с вами уже сталкивались. Параметры могут стоять как в подынтегральном выражении, так и (для определенных интегралов) в границах интегрирования. Вы можете применять любые обозначения для параметров (лучше, конечно, чтобы они не конфликтовали со встроенными переменными среды MathCAD — но в случае конфликта MathCAD вам сам об этом сообщит). Для работы с интегралами с параметрами вам, конечно же, придется использовать только аналитические способы интегрирования.
Напоследок еще совсем чуть-чуть поговорим про интегралы с параметрами. Почему чуть-чуть? Да потому, что работать с ними в MathCAD'е ничуть не сложнее, чем со всеми остальными типами интегралов, с которыми мы с вами уже сталкивались. Параметры могут стоять как в подынтегральном выражении, так и (для определенных интегралов) в границах интегрирования. Вы можете применять любые обозначения для параметров (лучше, конечно, чтобы они не конфликтовали со встроенными переменными среды MathCAD — но в случае конфликта MathCAD вам сам об этом сообщит). Для работы с интегралами с параметрами вам, конечно же, придется использовать только аналитические способы интегрирования.
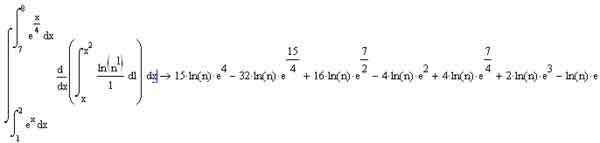 Мощь среды MathCAD позволяет вам в процессе интегрирования использовать самые разнообразные операторы для получения значений интегралов — вы можете использовать интегралы для вычисления границ интегрирования других интегралов, дифференцировать подынтегральные выражения и делать многое другое, вычисляя при этом интегралы и с использованием параметров. На иллюстрации видно, что MathCAD легко справился с "трехэтажным" интегралом, который содержит в себе все эти элементы.
Мощь среды MathCAD позволяет вам в процессе интегрирования использовать самые разнообразные операторы для получения значений интегралов — вы можете использовать интегралы для вычисления границ интегрирования других интегралов, дифференцировать подынтегральные выражения и делать многое другое, вычисляя при этом интегралы и с использованием параметров. На иллюстрации видно, что MathCAD легко справился с "трехэтажным" интегралом, который содержит в себе все эти элементы.
Что ж, вот мы с вами, пожалуй, и разобрались с таким важным аспектом применения среды MathCAD, как работа с производными, пределами, рядами, интегралами — словом, со всем тем, что в ВУЗовском курсе математики зовется математическим анализом. Как видите, MathCAD способен сильно облегчить жизнь студенту, который борется с интегралами для написания курсовой, или даже профессору, который использует методы математического анализа в своей научной работе.
SF, spaceflyer@tut.by
Несобственные интегралы
Перед тем, как углубляться во внутренние процессы вычисления интегралов численными методами, стоит немного поговорить о вычислении несобственных интегралов. Тема эта, впрочем, совсем не сложная, а потому и говорить о них мы с вами будем совсем чуть-чуть.
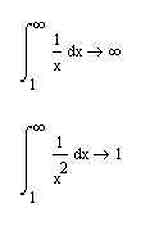

Кухня численного интегрирования
В общем и целом вычисление интегралов численными методами — это фактически использование математического определения (простите за тавтологию) определенного интеграла. Что это значит? Давайте попробуем вспомнить, как трактуются определенные интегралы с точки зрения математического анализа.


В MathCAD основным алгоритмом, используемым при численном интегрировании, является алгоритм, основанный как раз на использовании трапеций — этот метод вычисления определенных интегралов называется методом Ромберга. Есть в MathCAD и другой численный метод, используемый для вычисления интегралов от быстро изменяющихся функций — его разработчики этого математического пакета называли адаптивным. Его отличие от метода Ромберга заключается в том, что шаг разбиения интервала, на котором производится интегрирование, изменяется в соответствии со скоростью изменения значения самой функции, что позволяет дополнительно минимизировать погрешность. Еще одно преимущество этого метода интегрирования заключается в том, что мы можем с его помощью хорошо управляться с разрывами первого рода, которые при использовании метода Ромберга часто вообще приводят к тому, что функцию становится невозможным проинтегрировать численно. Напомню, что разрывом первого рода называется точка, для которой правосторонний и левосторонний пределы функции не равны друг другу, но при этом конечны. Если же хотя бы один из пределов бесконечен, то тогда точка называется разрывом второго рода.

Вы наверняка заметили, что, кроме метода Ромберга и адаптивного метода вычисления интегралов, в контекстном меню можно выбрать еще два других метода — Infinite Limit и Singular Endpoint. Эти методы используются для вычисления несобственных интегралов. Метод Singular Endpoint — это еще одна разновидность метода Ромберга, специально предназначенная для несобственных интегралов, а про Infinite Limit разработчики MathCAD распространяться по каким-то одним им известным причинам не захотели.
Интегралы с параметрами
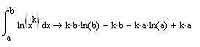
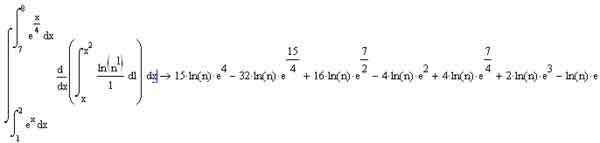
Что ж, вот мы с вами, пожалуй, и разобрались с таким важным аспектом применения среды MathCAD, как работа с производными, пределами, рядами, интегралами — словом, со всем тем, что в ВУЗовском курсе математики зовется математическим анализом. Как видите, MathCAD способен сильно облегчить жизнь студенту, который борется с интегралами для написания курсовой, или даже профессору, который использует методы математического анализа в своей научной работе.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 27 за 2008 год в рубрике soft


