MathCAD — это просто! Часть 13. Продолжаем бороться с дифференциальным исчислением
В прошлый раз мы с вами научились использовать возможности мощнейшей математической среды MathCAD для вычисления различных вещей, относящихся к дифференциальному исчислению: пределов, производных, сумм сходящихся числовых и функциональных рядов. Сегодня мы с вами продолжим знакомство с тем, как в MathCAD вычислять многие важные вещи из ВУЗовского курса математического анализа. Надеюсь, что это будет для вас достаточно интересно.
Вычисление частных производных
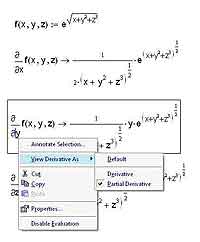 Напомню на всякий случай, что частными называются производные от функций нескольких переменных, берущиеся по одной или нескольким переменным. Для вычисления частных производных в MathCAD'е используются те же самые операторы, которые мы с вами уже весьма успешно применяли для вычисления полных производных. Единственное отличие — это, конечно же, оформление оператора взятия производной. В математическом анализе для отличия частных производных от полных используется специальная запись, в которой буква d, обозначающая производную, и сверху, и снизу пишется наклонной. MathCAD, как и во всех остальных случаях, позволяет пользователю применять привычную запись. Для того, чтобы изменить внешний вид оператора производной, выделите выражение и кликните по нему правой кнопкой мыши. В появившемся контекстном меню нужно выбрать пункт View Derivative As (Показывать производную как…), а в нем — Partial Derivative (Частная производная). Вы всегда можете вернуться к обычному отображению оператора производной, выбрав в том же самом меню пункт Derivative (Производная), который устанавливает для оператора производной вид оператора полной производной. Обратите внимание на то, что установка вида одного оператора взятия производной никак не влияет на все остальные операторы, как уже имеющиеся в вашей рабочей области, так и на те, которые будут добавлены в нее позднее.
Напомню на всякий случай, что частными называются производные от функций нескольких переменных, берущиеся по одной или нескольким переменным. Для вычисления частных производных в MathCAD'е используются те же самые операторы, которые мы с вами уже весьма успешно применяли для вычисления полных производных. Единственное отличие — это, конечно же, оформление оператора взятия производной. В математическом анализе для отличия частных производных от полных используется специальная запись, в которой буква d, обозначающая производную, и сверху, и снизу пишется наклонной. MathCAD, как и во всех остальных случаях, позволяет пользователю применять привычную запись. Для того, чтобы изменить внешний вид оператора производной, выделите выражение и кликните по нему правой кнопкой мыши. В появившемся контекстном меню нужно выбрать пункт View Derivative As (Показывать производную как…), а в нем — Partial Derivative (Частная производная). Вы всегда можете вернуться к обычному отображению оператора производной, выбрав в том же самом меню пункт Derivative (Производная), который устанавливает для оператора производной вид оператора полной производной. Обратите внимание на то, что установка вида одного оператора взятия производной никак не влияет на все остальные операторы, как уже имеющиеся в вашей рабочей области, так и на те, которые будут добавлены в нее позднее.
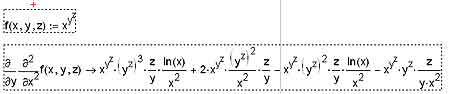 Что касается такой весьма и весьма немаловажной вещи, как взятие смешанных производных, то она реализуется с помощью последовательного взятия частных производных по разным переменным. Хотя, конечно, в результате могут получаться и довольно громоздкие выражения, как, например, на иллюстрации, демонстрирующей применение нескольких операторов взятия производной для вычисления смешанных производных.
Что касается такой весьма и весьма немаловажной вещи, как взятие смешанных производных, то она реализуется с помощью последовательного взятия частных производных по разным переменным. Хотя, конечно, в результате могут получаться и довольно громоздкие выражения, как, например, на иллюстрации, демонстрирующей применение нескольких операторов взятия производной для вычисления смешанных производных.
Неопределенные интегралы
Дифференцирование в математическом анализе неразрывно связано с интегрированием. Эти обратные друг другу действия — две стороны одной медали, а потому и мы с вами, поговорив об одном из них, перейдем к разговору о втором. У математиков есть шутка, что дифференцирование — это ремесло, а интегрирование — это искусство. MathCAD позволяет и интегрирование свести к уровню ремесла — если, конечно же, представлять себе, что в принципе может быть решаемо с помощью этой программы, а что нужно довести до того вида, в котором задачу уже можно "скармливать" MathCAD'у. Задача вычисления неопределенного интеграла обратна задаче нахождения производной функции. Неопределенный интеграл имеет также название первообразной, которое по ряду причин используется реже. Для вычисления неопределенных интегралов в среде MathCAD используется оператор, который можно легко найти на панели Calculus. Под знаком интеграла пользователь должен ввести функцию, для которой он хочет найти первообразную, а после знака дифференциала — переменную, по которой будет производиться интегрирование. Как видите, и здесь MathCAD верен себе, то есть дает пользователю возможность использовать, опять-таки, знакомые по математическому анализу обозначения неопределенных интегралов. Нужно отметить также, что для неопределенных интегралов необходимо применять символьное вычисление выражений, то есть знак "стрелочки", а не знак равенства.
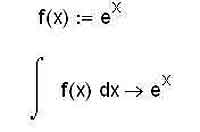 Следует, впрочем, помнить, что многие интегралы просто принципиально не выражаются в элементарных функциях. В том случае, если вы подсунули MathCAD'у один из таких весьма распространенных интегралов, ситуация может иметь два различных финала: либо MathCAD успешно проинтегрирует выражение и выдаст результат с использованием каких-либо специальных функций, либо же честно признается, что его такое интегрировать не учили. Во втором случае вы увидите после "стрелочки", стоящей за интегралом, запись вида indef_int(f(x), x). Естественно, вместо f(x) и x будут соответственно стоять подынтегральная функция и та переменная, по которой вы хотели провести интегрирование. Оба возможных варианта продемонстрированы на иллюстрации ниже.
Следует, впрочем, помнить, что многие интегралы просто принципиально не выражаются в элементарных функциях. В том случае, если вы подсунули MathCAD'у один из таких весьма распространенных интегралов, ситуация может иметь два различных финала: либо MathCAD успешно проинтегрирует выражение и выдаст результат с использованием каких-либо специальных функций, либо же честно признается, что его такое интегрировать не учили. Во втором случае вы увидите после "стрелочки", стоящей за интегралом, запись вида indef_int(f(x), x). Естественно, вместо f(x) и x будут соответственно стоять подынтегральная функция и та переменная, по которой вы хотели провести интегрирование. Оба возможных варианта продемонстрированы на иллюстрации ниже.
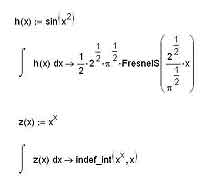 Со специальными функциями тоже все не так просто. Синтаксис, используемый для их записи в MathCAD'е, все же несколько отличается от принятого в математике, а потому, вполне вероятно, для того, чтобы разобраться в том, что за специальные функции скрываются за той или иной записью, придется воспользоваться справочной системой среды MathCAD. Для этого нажмите F1, в появившемся окне выберите вкладку Search, в поле рядом с кнопкой Go введите имя функции, информацию по которой вам нужно найти, а затем нажмите эту самую кнопку. Среди результатов поиска может оказаться и несколько разделов, и имеет смысл просмотреть их все.
Со специальными функциями тоже все не так просто. Синтаксис, используемый для их записи в MathCAD'е, все же несколько отличается от принятого в математике, а потому, вполне вероятно, для того, чтобы разобраться в том, что за специальные функции скрываются за той или иной записью, придется воспользоваться справочной системой среды MathCAD. Для этого нажмите F1, в появившемся окне выберите вкладку Search, в поле рядом с кнопкой Go введите имя функции, информацию по которой вам нужно найти, а затем нажмите эту самую кнопку. Среди результатов поиска может оказаться и несколько разделов, и имеет смысл просмотреть их все.
 В общем-то, даже в том случае, если MathCAD поднимает белый флаг при виде неопределенного интеграла, это не значит, что его вовсе невозможно вычислить в элементарных или специальных функциях. Вполне возможно, что с помощью каких-либо преобразований вам удастся привести его к виду, пригодному для решения в MathCAD. Также имеет смысл поискать решение в старых печатных справочниках или "погуглить" в интернете. Вполне возможно, что у MathCAD'а просто не хватило творческого воображения на то, чтобы до конца "раскрутить" ваш сложный интеграл.
В общем-то, даже в том случае, если MathCAD поднимает белый флаг при виде неопределенного интеграла, это не значит, что его вовсе невозможно вычислить в элементарных или специальных функциях. Вполне возможно, что с помощью каких-либо преобразований вам удастся привести его к виду, пригодному для решения в MathCAD. Также имеет смысл поискать решение в старых печатных справочниках или "погуглить" в интернете. Вполне возможно, что у MathCAD'а просто не хватило творческого воображения на то, чтобы до конца "раскрутить" ваш сложный интеграл.
Определенные интегралы
Неопределенные интегралы — это, конечно же, хорошо, но все же на практике куда как чаще используются интегралы определенные. И, думаю, для вас не окажется неожиданностью тот факт, что MathCAD прекрасно умеет справляться и с этим видом интегралов. Определенный интеграл, как вы понимаете, отличается от неопределенного наличием пределов интегрирования. Фактически неопределенный интеграл — это функция (первообразная подынтегральной функции), в то время как определенный интеграл — это просто какое-то число. То есть его мы можем вычислить не только аналитически, но и численно, что позволяет нам рассчитывать значения определенных интегралов даже тогда, когда первообразная рассчитана быть не может. Оператор для расчета определенных интегралов в MathCAD'е находится на панели Calculus недалеко от оператора расчета неопределенных интегралов и отличается от него, как я уже совсем недавно говорил, наличием пределов сверху и снизу от символа интеграла. После того, как вы запишете подынтегральное выражение, переменную интегрирования и собственно пределы, можно ставить знак равенства или стрелочку для вычисления определенного интеграла. В первом случае интеграл будет вычислен численно, во втором — аналитически.
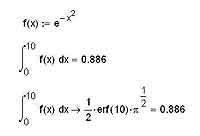 Вопрос о том, какой способ вычисления интегралов использовать: численный или аналитический, — не такой надуманный и праздный, как может сначала показаться. Дело в том, что аналитически определенные интегралы вычисляются, во-первых, точнее, а во-вторых, быстрее, нежели численно. Правда, может возникнуть ситуация, аналогичная той, которую вы можете увидеть на иллюстрации выше — то есть символьный процессор не доведет процесс вычислений до конца, а оставит интеграл в виде смеси численных значений и функций. Впрочем, с этим всегда довольно просто справиться, как видите. Для вычисления кратных интегралов используется тот же прием, что и для вычисления смешанных частных производных для функций многих переменных. То есть мы последовательно интегрируем несколько раз функцию с заданными пределами, и в результате получаем именно то, что, в общем- то, и рассчитывали получить. Стоит отметить, что, поскольку при интегрировании кратных интегралов мы теряем при численном интегрировании особенно много времени, то здесь особенно желательно использовать именно аналитический способ вычисления интегралов.
Вопрос о том, какой способ вычисления интегралов использовать: численный или аналитический, — не такой надуманный и праздный, как может сначала показаться. Дело в том, что аналитически определенные интегралы вычисляются, во-первых, точнее, а во-вторых, быстрее, нежели численно. Правда, может возникнуть ситуация, аналогичная той, которую вы можете увидеть на иллюстрации выше — то есть символьный процессор не доведет процесс вычислений до конца, а оставит интеграл в виде смеси численных значений и функций. Впрочем, с этим всегда довольно просто справиться, как видите. Для вычисления кратных интегралов используется тот же прием, что и для вычисления смешанных частных производных для функций многих переменных. То есть мы последовательно интегрируем несколько раз функцию с заданными пределами, и в результате получаем именно то, что, в общем- то, и рассчитывали получить. Стоит отметить, что, поскольку при интегрировании кратных интегралов мы теряем при численном интегрировании особенно много времени, то здесь особенно желательно использовать именно аналитический способ вычисления интегралов.
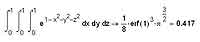 В применении системы MathCAD для расчета определенных интегралов есть немало тонких моментов, которые не возникали при расчете интегралов неопределенных. Особенно это касается численных методов расчета интегралов. Как я уже говорил, эти методы позволяют рассчитать даже такие интегралы, которые не поддаются аналитическому вычислению. Однако за все надо платить, а потому использование численных методов интегрирования способно приводить к значительным погрешностям в результате, что, сами понимаете, при решении весьма значительного по своей распространенности класса задач не просто нежелательно, а часто даже совершенно недопустимо. О погрешностях при численном интегрировании в MathCAD'е и о том, как избежать того, чтобы они стали совсем уж гигантскими, мы с вами поговорим в следующий раз. А пока что давайте подведем итоги тому, о чем мы говорили сегодня.
В применении системы MathCAD для расчета определенных интегралов есть немало тонких моментов, которые не возникали при расчете интегралов неопределенных. Особенно это касается численных методов расчета интегралов. Как я уже говорил, эти методы позволяют рассчитать даже такие интегралы, которые не поддаются аналитическому вычислению. Однако за все надо платить, а потому использование численных методов интегрирования способно приводить к значительным погрешностям в результате, что, сами понимаете, при решении весьма значительного по своей распространенности класса задач не просто нежелательно, а часто даже совершенно недопустимо. О погрешностях при численном интегрировании в MathCAD'е и о том, как избежать того, чтобы они стали совсем уж гигантскими, мы с вами поговорим в следующий раз. А пока что давайте подведем итоги тому, о чем мы говорили сегодня.
Как видите, MathCAD с легкостью справляется с интегралами — пусть не со всеми, но с их значительной частью. Тех возможностей этой великолепной среды, о которых мы с вами уже успели поговорить в цикле статей "MathCAD — это просто!", на мой взгляд, как раз достаточно для того, чтобы прибавить вам энтузиазма в дальнейшем изучении этой программы.
SF, spaceflyer@tut.by
Вычисление частных производных

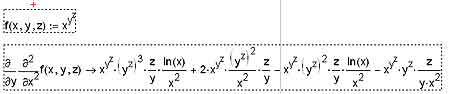
Неопределенные интегралы
Дифференцирование в математическом анализе неразрывно связано с интегрированием. Эти обратные друг другу действия — две стороны одной медали, а потому и мы с вами, поговорив об одном из них, перейдем к разговору о втором. У математиков есть шутка, что дифференцирование — это ремесло, а интегрирование — это искусство. MathCAD позволяет и интегрирование свести к уровню ремесла — если, конечно же, представлять себе, что в принципе может быть решаемо с помощью этой программы, а что нужно довести до того вида, в котором задачу уже можно "скармливать" MathCAD'у. Задача вычисления неопределенного интеграла обратна задаче нахождения производной функции. Неопределенный интеграл имеет также название первообразной, которое по ряду причин используется реже. Для вычисления неопределенных интегралов в среде MathCAD используется оператор, который можно легко найти на панели Calculus. Под знаком интеграла пользователь должен ввести функцию, для которой он хочет найти первообразную, а после знака дифференциала — переменную, по которой будет производиться интегрирование. Как видите, и здесь MathCAD верен себе, то есть дает пользователю возможность использовать, опять-таки, знакомые по математическому анализу обозначения неопределенных интегралов. Нужно отметить также, что для неопределенных интегралов необходимо применять символьное вычисление выражений, то есть знак "стрелочки", а не знак равенства.
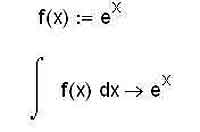
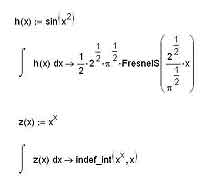

Определенные интегралы
Неопределенные интегралы — это, конечно же, хорошо, но все же на практике куда как чаще используются интегралы определенные. И, думаю, для вас не окажется неожиданностью тот факт, что MathCAD прекрасно умеет справляться и с этим видом интегралов. Определенный интеграл, как вы понимаете, отличается от неопределенного наличием пределов интегрирования. Фактически неопределенный интеграл — это функция (первообразная подынтегральной функции), в то время как определенный интеграл — это просто какое-то число. То есть его мы можем вычислить не только аналитически, но и численно, что позволяет нам рассчитывать значения определенных интегралов даже тогда, когда первообразная рассчитана быть не может. Оператор для расчета определенных интегралов в MathCAD'е находится на панели Calculus недалеко от оператора расчета неопределенных интегралов и отличается от него, как я уже совсем недавно говорил, наличием пределов сверху и снизу от символа интеграла. После того, как вы запишете подынтегральное выражение, переменную интегрирования и собственно пределы, можно ставить знак равенства или стрелочку для вычисления определенного интеграла. В первом случае интеграл будет вычислен численно, во втором — аналитически.
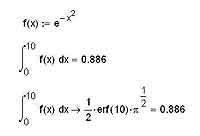
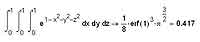
Как видите, MathCAD с легкостью справляется с интегралами — пусть не со всеми, но с их значительной частью. Тех возможностей этой великолепной среды, о которых мы с вами уже успели поговорить в цикле статей "MathCAD — это просто!", на мой взгляд, как раз достаточно для того, чтобы прибавить вам энтузиазма в дальнейшем изучении этой программы.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 26 за 2008 год в рубрике soft


