MathCAD — это просто! Часть 9. Неравенства
Неравенства бывают разные — это всем известно еще со школьной скамьи. Есть социальные и расовые неравенства, неравенство полов и возрастов, неравенство возможностей и целей. Но мы с вами будем говорить о совсем других неравенствах, которые не имеют ничего общего с упомянутыми выше явлениями. То есть дело мы сейчас с вами будем иметь, как вы, должно быть, уже догадались, с неравенствами алгебраическими.
Я хотел рассказать о неравенствах уже давно, но как-то переключился на графики, а потому ушел немного в сторону. Сейчас мы с вами как бы вернемся немного назад, к уравнениям, и посмотрим, насколько решение неравенств в MathCAD'е отличается от решения уравнений. Надеюсь, что вы еще не совсем забыли, каким именно образом мы их решали — впрочем, даже если и так, всегда можно поднять подшивку КГ и посмотреть, что именно рассказывалось в любой из предыдущих частей серии "MathCAD — это просто". Ну и, конечно же, некоторые вещи я буду напоминать прямо по ходу дела. Так что не будем больше откладывать дело в долгий ящик, а примемся вместо этого, засучив рукава, упоенно решать, решать, решать неравенства.
Решение неравенств
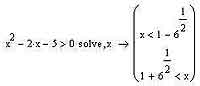 Неравенство, вообще говоря, вещь более сложная, чем уравнение, в силу того простого факта, что мы часто имеем дело с необходимостью исследования функции на всей числовой оси. Поэтому особенно соблазнительно переложить на MathCAD столь нудную и неприятную работу. Думаю, для вас не станет откровением то, что использовать для решения неравенств можно solve — точно так же, как и для решения уравнений. Порядок действий совершенно аналогичен уже изученному нами ранее: записываем собственно неравенство (к примеру, пусть это будет x2+2x-5>0), нажимаем solve на панели Symbolic и, как говорится, наслаждаемся полученным результатом. На рисунке вы можете увидеть, что, как и следовало ожидать, то неравенство, которым мы загрузили MathCAD, он разгрыз как орешек.
Неравенство, вообще говоря, вещь более сложная, чем уравнение, в силу того простого факта, что мы часто имеем дело с необходимостью исследования функции на всей числовой оси. Поэтому особенно соблазнительно переложить на MathCAD столь нудную и неприятную работу. Думаю, для вас не станет откровением то, что использовать для решения неравенств можно solve — точно так же, как и для решения уравнений. Порядок действий совершенно аналогичен уже изученному нами ранее: записываем собственно неравенство (к примеру, пусть это будет x2+2x-5>0), нажимаем solve на панели Symbolic и, как говорится, наслаждаемся полученным результатом. На рисунке вы можете увидеть, что, как и следовало ожидать, то неравенство, которым мы загрузили MathCAD, он разгрыз как орешек.
Пожалуй, единственный минус, который можно назвать — это то, что функция solve выдает ответы в несколько непривычном виде. То есть результат она записывает в виде вектора элементарных неравенств в то время, как удобнее бывает его записать в виде двойного неравенства или в виде интервала. Однако, глядя на рисунок, думаю, вы согласитесь со мной в том, что привести результат в удобный для человеческого глаза вид не составит никакого труда. Нужно только иметь в виду, что, если в результате вычисления решения MathCAD пришел к выводу, что данному неравенству удовлетворяет любое рациональное число, то в ответе напишет просто обозначение той переменной, относительно которой мы решали неравенство — то есть в нашем случае MathCAD написал бы, если бы было нужно, просто x. При интерпретации решений нужно внимательно следить за тем, какой именно знак (знак точного неравенства или приблизительного, то есть с возможностью равенства) используется системой в ответе: даже если из всей числовой оси не подходит всего лишь одна-единственная точка, MathCAD не выдаст вам ответ в виде x?a, а напишет в столбик два неравенства: x<a и x>a.
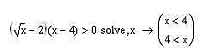 Но если бы вывод результатов был единственным минусом всего процесса решения неравенств в MathCAD'е, то о нем, пожалуй, не стоило бы даже и вспоминать. К сожалению, есть вещи гораздо более серьезные, которые не позволяют использовать результаты решения неравенств в MathCAD'е без их предварительной проверки. Дело в том, что MathCAD не умеет грамотно работать с областью определения той переменной, которая используется в неравенстве. Это, конечно, бывает не во всех случаях — например, когда область определения ограничивается тем фактом, что неравенство у нас записано в виде дроби, но при этом и числитель, и знаменатель содержат многочлены целых степеней, то MathCAD вполне успешно справляется с такими задачами. Однако уже наличие корней в неравенстве ставит MathCAD в тупик: программа вполне может выдать результат, для которого под корнем оказываются отрицательные значения переменных в то время, как на множестве рациональных чисел вычисление корня отрицательной величины не определено. За примером подобного случая далеко ходить не надо: давайте попробуем подсунуть функции solve неравенство (x1/2-2)(x-4)>0. В качестве результата MathCAD безо всяких зазрений совести выдает ответ, который можно записать как x?4 (см. иллюстрацию). Если бы в нашем неравенстве не было корня, то этот ответ, конечно, был бы совершенно верен, однако, поскольку корень все-таки присутствует, то и ответ этот верным считать, к сожалению, никоим образом не удается.
Но если бы вывод результатов был единственным минусом всего процесса решения неравенств в MathCAD'е, то о нем, пожалуй, не стоило бы даже и вспоминать. К сожалению, есть вещи гораздо более серьезные, которые не позволяют использовать результаты решения неравенств в MathCAD'е без их предварительной проверки. Дело в том, что MathCAD не умеет грамотно работать с областью определения той переменной, которая используется в неравенстве. Это, конечно, бывает не во всех случаях — например, когда область определения ограничивается тем фактом, что неравенство у нас записано в виде дроби, но при этом и числитель, и знаменатель содержат многочлены целых степеней, то MathCAD вполне успешно справляется с такими задачами. Однако уже наличие корней в неравенстве ставит MathCAD в тупик: программа вполне может выдать результат, для которого под корнем оказываются отрицательные значения переменных в то время, как на множестве рациональных чисел вычисление корня отрицательной величины не определено. За примером подобного случая далеко ходить не надо: давайте попробуем подсунуть функции solve неравенство (x1/2-2)(x-4)>0. В качестве результата MathCAD безо всяких зазрений совести выдает ответ, который можно записать как x?4 (см. иллюстрацию). Если бы в нашем неравенстве не было корня, то этот ответ, конечно, был бы совершенно верен, однако, поскольку корень все-таки присутствует, то и ответ этот верным считать, к сожалению, никоим образом не удается.
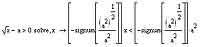 Другая проблема, которая может возникнуть при решении неравенств (как, впрочем, и в решении уравнений) — это громоздкость выдаваемых системой в ответе выражений. Правда, для тех случаев, когда мы записываем все коэффициенты в выражениях непосредственно в числовом виде, это менее заметно, поскольку и ответ система выдает в виде чисел. Однако, если перейти от конкретных чисел к общему виду неравенств, то получится все как-то уже не так весело и жизнерадостно. Чтобы не быть голословным, приведу, как издавна уже у нас с вами повелось, пример, иллюстрирующий последние высказывания. Эта иллюстрация показывает, как MathCAD решал неравенство x1/2-a>0.
Другая проблема, которая может возникнуть при решении неравенств (как, впрочем, и в решении уравнений) — это громоздкость выдаваемых системой в ответе выражений. Правда, для тех случаев, когда мы записываем все коэффициенты в выражениях непосредственно в числовом виде, это менее заметно, поскольку и ответ система выдает в виде чисел. Однако, если перейти от конкретных чисел к общему виду неравенств, то получится все как-то уже не так весело и жизнерадостно. Чтобы не быть голословным, приведу, как издавна уже у нас с вами повелось, пример, иллюстрирующий последние высказывания. Эта иллюстрация показывает, как MathCAD решал неравенство x1/2-a>0.
 Выражение, выдаваемое MathCAD'ом результате борьбы с этим неравенством, настолько громоздкое, что даже сложно сходу оценить его правильность. В будущем мы с вами посмотрим, как можно бороться с громоздкостью выражений, используя мощь символьного процессора, встроенного в MathCAD его разработчиками, но заранее хочу сказать, что серьезно упростить с его помощью удается сравнительно небольшое число разнообразных выражений. Что это значит? Это значит, что с неравенствами лучше не увлекаться получением решения в общем виде, а решать, используя конкретные значения коэффициентов, и тогда работать с результатами решений, выдаваемыми MathCAD'ом, будет существенно проще и удобнее. Но самого грустного в песне о решении неравенств мы еще не касались. Оно же состоит в том, что даже не со всеми элементарными функциями MathCAD справляется успешно, не говоря уже о функциях специальных. Так, скажем, символьный процессор MathCAD, который и использует функция solve, "не дружит" с тригонометрическими функциями. Верится с трудом, но это так — при всей своей мощи MathCAD не может решить даже элементарное школьное неравенство sin(x)<0 (см. иллюстрацию). С неравенством sin(x)>0 у системы, как вы понимаете, тоже возникают немалые проблемы.
Выражение, выдаваемое MathCAD'ом результате борьбы с этим неравенством, настолько громоздкое, что даже сложно сходу оценить его правильность. В будущем мы с вами посмотрим, как можно бороться с громоздкостью выражений, используя мощь символьного процессора, встроенного в MathCAD его разработчиками, но заранее хочу сказать, что серьезно упростить с его помощью удается сравнительно небольшое число разнообразных выражений. Что это значит? Это значит, что с неравенствами лучше не увлекаться получением решения в общем виде, а решать, используя конкретные значения коэффициентов, и тогда работать с результатами решений, выдаваемыми MathCAD'ом, будет существенно проще и удобнее. Но самого грустного в песне о решении неравенств мы еще не касались. Оно же состоит в том, что даже не со всеми элементарными функциями MathCAD справляется успешно, не говоря уже о функциях специальных. Так, скажем, символьный процессор MathCAD, который и использует функция solve, "не дружит" с тригонометрическими функциями. Верится с трудом, но это так — при всей своей мощи MathCAD не может решить даже элементарное школьное неравенство sin(x)<0 (см. иллюстрацию). С неравенством sin(x)>0 у системы, как вы понимаете, тоже возникают немалые проблемы.
Возможно, вас несколько утешит мысль о том, что с показательными и логарифмическими неравенствами MathCAD справляется все-таки неплохо (правда, и здесь есть ограничение — случаи, когда переменная, стоящая в основании степенной функции, в том или ином виде попадает и в показатель). Однако и с тригонометрическими неравенствами ведь что-то нужно делать, не так ли? Действительно, способ решить сложное тригонометрическое неравенство существует — это преобразовать его таким образом, чтобы оно содержало одноименные тригонометрические функции (обычно синусы или косинусы, хотя, возможно, также и тангенсы или котангенсы — это уже зависит от вашего вкуса и от вида конкретного неравенства), а затем уже решать, но не относительно x, а относительно той функции, которая является для вашего получившегося неравенства базовой. О преобразовании выражений встроенными средствами MathCAD мы, как я уже, кажется, обещал выше, поговорим, а пока просто имейте в виду, что можно применять такой прием борьбы с тригонометрическими неравенствами. Но, к сожалению, неравенства sin(x) > 0 и sin(x) < 0 придется все же решать вручную.
Системы неравенств
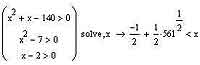 Неравенства могут быть записаны и в виде системы. Если вы помните, как мы справлялись с решением систем уравнений, то и работа с системами неравенств не должна показаться для вас особенно сложной, поскольку в большинстве случаев она совершенно аналогична работе с системами уравнений. Мы записываем систему неравенств виде вектор-столбца, который потом решаем с помощью функции solve совершенно аналогично тому, как решали одиночное неравенство.
Неравенства могут быть записаны и в виде системы. Если вы помните, как мы справлялись с решением систем уравнений, то и работа с системами неравенств не должна показаться для вас особенно сложной, поскольку в большинстве случаев она совершенно аналогична работе с системами уравнений. Мы записываем систему неравенств виде вектор-столбца, который потом решаем с помощью функции solve совершенно аналогично тому, как решали одиночное неравенство.
Этот метод решения систем неравенств, безусловно, подкупает, прежде всего, своей простотой, однако, сами понимаете, у всего на свете есть свои минусы (или, как сказал герой фильма "В джазе только девушки", "У всех свои недостатки"). Бывают случаи, когда solve в бессилии опускает руки перед не самой сложной системой неравенств, и тогда приходится изобретать какие-то специальные методы, которые позволили бы нам получить решение нужной системы. К счастью, ничего экстраординарного изобретать, на самом-то деле, не требуется, поскольку алгебраические неравенства обладают счастливым свойством, позволяющим нам разбить решение на несколько этапов. То есть мы можем решить каждое из неравенств системы по отдельности, а потом просто объединить результаты так, как этому учили еще в школе. То есть мы должны выбрать из всех результатов решения неравенств те промежутки, на которых наша переменная удовлетворяет каждому из наших неравенств. Сделать это, как правило, не так уж и сложно. Возможно, решение системы неравенств вторым, пошаговым, способом можно считать даже более предпочтительным путем, чем "скармливание" функции solve всей системы сразу, потому что путем преобразования мы всегда сможем добиться того, чтобы MathCAD справился с неравенством, а значит, что такой метод подходит для всех неравенств. Функция solve же, к сожалению, творческими задатками не обладает, а потому априори метод действия "в лоб", который мы применяем, используя ее ко всей системе, менее результативен, чем пошаговое решение каждого из неравенств с последующим объединением ответов. Но, конечно, какой из методов использовать сразу — это все остается на ваше собственное усмотрение.
Итак, мы с вами познакомились с методами решения неравенств в среде MathCAD. Как видите, реализация решений их в MathCAD'е, скажем прямо, довольно-таки далека еще от совершенства, но, тем не менее, применяя природную смекалку и некоторые математические хитрости, можно успешно справляться с большинством видов неравенств и их систем (ну, разве что придется решать вручную простые тригонометрические неравенства — но это не так уж и страшно, на самом-то деле). Но в общем и целом, несмотря на все трудности, с которыми столкнется пользователь, пожелавший озадачить MathCAD неравенствами, без MathCAD'а решать их будет, как ни крути, дольше.
SF, spaceflyer@tut.by
Я хотел рассказать о неравенствах уже давно, но как-то переключился на графики, а потому ушел немного в сторону. Сейчас мы с вами как бы вернемся немного назад, к уравнениям, и посмотрим, насколько решение неравенств в MathCAD'е отличается от решения уравнений. Надеюсь, что вы еще не совсем забыли, каким именно образом мы их решали — впрочем, даже если и так, всегда можно поднять подшивку КГ и посмотреть, что именно рассказывалось в любой из предыдущих частей серии "MathCAD — это просто". Ну и, конечно же, некоторые вещи я буду напоминать прямо по ходу дела. Так что не будем больше откладывать дело в долгий ящик, а примемся вместо этого, засучив рукава, упоенно решать, решать, решать неравенства.
Решение неравенств
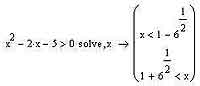
Пожалуй, единственный минус, который можно назвать — это то, что функция solve выдает ответы в несколько непривычном виде. То есть результат она записывает в виде вектора элементарных неравенств в то время, как удобнее бывает его записать в виде двойного неравенства или в виде интервала. Однако, глядя на рисунок, думаю, вы согласитесь со мной в том, что привести результат в удобный для человеческого глаза вид не составит никакого труда. Нужно только иметь в виду, что, если в результате вычисления решения MathCAD пришел к выводу, что данному неравенству удовлетворяет любое рациональное число, то в ответе напишет просто обозначение той переменной, относительно которой мы решали неравенство — то есть в нашем случае MathCAD написал бы, если бы было нужно, просто x. При интерпретации решений нужно внимательно следить за тем, какой именно знак (знак точного неравенства или приблизительного, то есть с возможностью равенства) используется системой в ответе: даже если из всей числовой оси не подходит всего лишь одна-единственная точка, MathCAD не выдаст вам ответ в виде x?a, а напишет в столбик два неравенства: x<a и x>a.
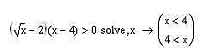


Возможно, вас несколько утешит мысль о том, что с показательными и логарифмическими неравенствами MathCAD справляется все-таки неплохо (правда, и здесь есть ограничение — случаи, когда переменная, стоящая в основании степенной функции, в том или ином виде попадает и в показатель). Однако и с тригонометрическими неравенствами ведь что-то нужно делать, не так ли? Действительно, способ решить сложное тригонометрическое неравенство существует — это преобразовать его таким образом, чтобы оно содержало одноименные тригонометрические функции (обычно синусы или косинусы, хотя, возможно, также и тангенсы или котангенсы — это уже зависит от вашего вкуса и от вида конкретного неравенства), а затем уже решать, но не относительно x, а относительно той функции, которая является для вашего получившегося неравенства базовой. О преобразовании выражений встроенными средствами MathCAD мы, как я уже, кажется, обещал выше, поговорим, а пока просто имейте в виду, что можно применять такой прием борьбы с тригонометрическими неравенствами. Но, к сожалению, неравенства sin(x) > 0 и sin(x) < 0 придется все же решать вручную.
Системы неравенств
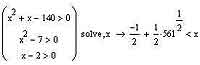
Этот метод решения систем неравенств, безусловно, подкупает, прежде всего, своей простотой, однако, сами понимаете, у всего на свете есть свои минусы (или, как сказал герой фильма "В джазе только девушки", "У всех свои недостатки"). Бывают случаи, когда solve в бессилии опускает руки перед не самой сложной системой неравенств, и тогда приходится изобретать какие-то специальные методы, которые позволили бы нам получить решение нужной системы. К счастью, ничего экстраординарного изобретать, на самом-то деле, не требуется, поскольку алгебраические неравенства обладают счастливым свойством, позволяющим нам разбить решение на несколько этапов. То есть мы можем решить каждое из неравенств системы по отдельности, а потом просто объединить результаты так, как этому учили еще в школе. То есть мы должны выбрать из всех результатов решения неравенств те промежутки, на которых наша переменная удовлетворяет каждому из наших неравенств. Сделать это, как правило, не так уж и сложно. Возможно, решение системы неравенств вторым, пошаговым, способом можно считать даже более предпочтительным путем, чем "скармливание" функции solve всей системы сразу, потому что путем преобразования мы всегда сможем добиться того, чтобы MathCAD справился с неравенством, а значит, что такой метод подходит для всех неравенств. Функция solve же, к сожалению, творческими задатками не обладает, а потому априори метод действия "в лоб", который мы применяем, используя ее ко всей системе, менее результативен, чем пошаговое решение каждого из неравенств с последующим объединением ответов. Но, конечно, какой из методов использовать сразу — это все остается на ваше собственное усмотрение.
Итак, мы с вами познакомились с методами решения неравенств в среде MathCAD. Как видите, реализация решений их в MathCAD'е, скажем прямо, довольно-таки далека еще от совершенства, но, тем не менее, применяя природную смекалку и некоторые математические хитрости, можно успешно справляться с большинством видов неравенств и их систем (ну, разве что придется решать вручную простые тригонометрические неравенства — но это не так уж и страшно, на самом-то деле). Но в общем и целом, несмотря на все трудности, с которыми столкнется пользователь, пожелавший озадачить MathCAD неравенствами, без MathCAD'а решать их будет, как ни крути, дольше.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 21 за 2008 год в рубрике soft


