MathCAD — это просто! Часть 8. Графики векторных полей и анимированные графики

Во многих учебниках по MathCAD'у сведения о визуализации векторных полей по какой-то причине отсутствуют. Сложно сказать, чем руководствовались их авторы — ведь эта тема очень и очень важна для многих пользователей того всесторонне замечательного математического пакета, который мы с вами так усердно изучаем. Вполне возможно, что авторы считают тему не слишком актуальной для технических специалистов — однако хочу заметить, что это совсем не так, ведь для расчета огромного количества реальных вещей используется такая математическая модель, как векторное поле. Достаточно вспомнить об электричестве — ведь все электродинамические расчеты основаны именно на математической теории векторного анализа, оперирующей векторными и скалярными полями. Обширно применяется эта теория и в других отраслях физики — например, в гидродинамике. В общем, как видите, полезность построения графиков трехмерных векторных полей вполне очевидна. Что касается самих методов векторного анализа, то их применительно к MathCAD'у мы рассмотрим все-таки позже.

Векторные поля

Прежде чем говорить о графиках векторных полей, стоит немного рассказать о том, что же представляют собой вот эти сами векторные поля. Если даже вы и хорошо знакомы с этой математической моделью, которая при ближайшем рассмотрении оказывается очень удобной и совсем не сложной, все равно небольшой ликбез никогда не повредит. Итак, векторное поле — это закон, по которому каждой точке пространства сопоставляется некоторый вектор. Обычно эти векторы направлены не хаотически, а образуют в пространстве некоторые фигуры, которые как раз и становятся видны в результате визуализации полей. Эти фигуры обусловлены некоторыми свойствами, характерными для определенных классов векторных полей, используемых более часто, чем векторные поля совершенно произвольные. Потенциальными называются такие векторные поля, которые описываются как градиент некоторой скалярной функции. Ротор (векторная производная) таких полей равна нулю. Существуют также соленоидальные векторные поля, дивергенция (скалярная производная) которых равна нулю. Не будем вдаваться в подробности и в математические формулы — вы легко сможете найти более подробную информацию об этих типах векторных полей практически в любом учебнике по матанализу или по электродинамике. Визуализация векторного поля — это отображение закономерности распределения векторов в нем на экране. Думаю, что не имеет смысла подробно рассказывать о том, как именно все отображается — вы сами все очень быстро поймете, когда увидите, как это делается в MathCAD'е.

Графики векторных полей

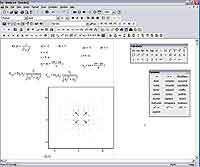Для построения графика векторного поля прежде всего нужно задать функцию, которую этот график будет в дальнейшем визуализировать — здесь, в общем-то, как видите, все так же, как с обычными трехмерными графиками. Функцию задайте скалярную и от двух переменных, которыми будут координаты x и y. Конечно, функцию можно выбрать практически любую, но хрестоматийным примером стала зависимость, аналогичная той, которую имеет напряженность электрического поля, создаваемого точечным зарядом: f(x, y) = 1 / (x2 + y2). Думаю, именно ее мы и будем использовать для построения нашего с вами первого графика векторного поля.

Собственно говоря, на этом сходство с обычным трехмерным графиком как бы и заканчивается, потому что дальше нужно вручную задать базис, в котором будут строиться векторы нашего с вами поля. Только сначала нужно задать сетку разбиения нашей области построения для этого поля (см. иллюстрацию). Она задается границами xa и xb, ya и yb, обозначающими, соответственно, наибольшее и наименьшее значение координат. Далее мы рассчитываем по предельно простым формулам равномерно распределенные между границами опорные точки, и рассчитываем значения векторов в этих точках. Вот на этом-то расчете, я так думаю, имеет смысл остановиться и подробнее. Как вы знаете, должно быть, каждый вектор имеет смысл только будучи построенным в определенном базисе. Базис — это линейно независимая система векторов, через которые может быть выражен любой другой вектор в данном пространстве. Что значит "линейно независимая"? Это значит, что в данной системе один вектор не может быть линейно выражен через другие, то есть сумма остальных векторов, умноженных на любые скалярные коэффициенты, никогда не даст этот самый вектор. В качестве базиса могут использоваться разные векторы. Чаще всего используется прямоугольная декартова система координат, в которой базисом являются векторы единичной длины, направленные вдоль координатных осей x, y и z. Однако все эти соображения никоим образом не помогают понять, каким должен быть базис для векторов, поле которых мы с вами сейчас строим. Ответ прост: в качестве базисных векторов используются линейно независимые векторы из градиента нашей скалярной функции, которую мы задавали в самом начале данного, с позволения сказать, упражнения. Градиент — это векторная производная скалярной функции, направленная в сторону ее убывания. Компоненты градиента направлены параллельно координатным осям, то есть в нашем случае мы можем просто написать в качестве базисных векторов X и Y компоненты градиента. Именно это и отражено на приведенной иллюстрации.

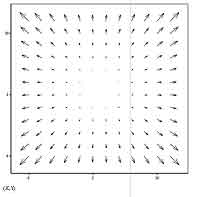К сожалению, по той же иллюстрации видно, что с построением векторного поля существует одна досадная, но практически неустранимая мелочь — векторы, отстоящие достаточно далеко от его силового центра, настолько малы, что MathCAD изображает их даже и не стрелками, а просто точками. Виноват здесь, впрочем, совсем не MathCAD, который просто максимально честно отображает то, что мы его попросили отобразить. Дело в том, что по мере удаления от силового центра (он у нас пришелся на начало координат) поле уменьшается обратно пропорционально квадрату расстояния до этого самого центра, то есть убывает модуль (длина) наших векторов очень и очень быстро. Чуть лучше их будет видно, если растянуть картинку до достаточно больших размеров (фактически лучше всего — на весь экран), но и это не спасает положения в целом. Так что приготовьтесь к тому, что зачастую визуализация векторных полей будет совсем не так хороша, как вам хотелось бы. Можно попробовать несколько улучшить ситуацию, поэкспериментировав с границами отображаемого участка векторного поля, однако и это, как правило, редко дает удовлетворительные результаты. Лучшим выходом будет логарифмирование входной скалярной функции, что будет гораздо лучше, однако в таком случае стоит помнить, что и график у нас получится в логарифмическом масштабе, а не в линейном. В качестве иллюстрации того, что картинка, получаемая в результате визуализации векторного поля больше зависит от функции, которая его задает, чем от размеров области отображения, приведу иллюстрацию векторного поля на участке х = (-50; 50), у = (-50; 50) и с f(x, y) = x2 + y2. Как видите, положение вещей кардинально отличается от того, что мы видели на рисунке, когда f(x, y) была записана как 1/(x2 + y2). Если вы попробуете для любого из этих случаев умножить каждую из границ диапазона отображения на какую-нибудь отличную от нуля произвольную константу, то увидите, что картинка никак не изменится. Думаю, вполне понятно, что это происходит потому, что MathCAD изображает относительную, а не абсолютную величину векторов поля.

Анимированные графики

Статические графики удобны для отображения статических моделей, то есть тех, где переменными величинами служат лишь пространственные координаты. Однако как же быть в том случае, если переменной становится и время? Вполне очевидный ответ — использовать для визуализации график, изменяющийся во времени, то есть анимированный. К счастью, MathCAD позволяет использовать и такие графики, ежели есть такая необходимость — как вы сможете самостоятельно убедиться, это, собственно, и не так сложно, как может показаться с первого взгляда. Для того, чтобы заставить какой- либо график стать анимированным, нужно, чтобы время (по традиции переменная, которая его обозначает, будет называться t) входило в функцию, график которой мы с вами будем строить, как параметр. Причем значение этого параметра следует определить заранее примерно следующим образом: t := FRAME/10. Здесь FRAME — это номер текущего кадра в анимации, а делим мы его на 10 для того, чтобы функция не возрастала очень быстро, и мы не получили ошибки во время ее построения, а также чтобы смотреть за процессом изменения графика во времени было удобнее. Впрочем, то, каким образом задавать зависимость хода времени от номера кадра, зависит исключительно от свойств вашей функции. Поскольку в моем примере время входит в показатель степени (как видите на рисунке, я для иллюстрации анимации выбрал функцию y = xt), то оно должно изменяться достаточно медленно, чтобы, как я уже сказал, все было без ошибок и выглядело презентабельно. Если же время у вас, наоборот, под логарифмом, то можно, напротив, домножать переменную FRAME на какую-нибудь константу, большую, чем единица. Можно, как видите, даже поэкспериментировать и задать нелинейный ход времени — все, как видите, очень легко настраивается, и можно наблюдать за множеством интересных и необычных вещей. Например, если сделать t := exp(FRAME), то вид графика получится в конце концов совсем не таким, какой был при линейной зависимости между временем и номером кадра (догадываетесь, почему так происходит?).

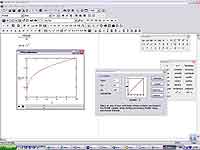Что делать дальше? О, все очень просто! Сначала строим график зависимости нашей функции от x. После заходим в меню Tools, далее в Animate и в появившемся подразделе меню выбираем Record (тот пункт, которой сбоку отмечен маленьким значком видеокамеры). Далее мышкой выделяем область графика и нажимаем на кнопку Animate в появившемся окне. Сначала MathCAD просчитает и отобразит анимацию в маленькой панельке предпросмотра, а потом выдаст на экран уже большое нормальное окно с графиком. Можно менять минимальное значения переменной FRAME в полях From и To соответственно, а в поле At можно менять скорость воспроизведения анимации (количество кадров, отображаемых программой в одну секунду).

Анимированный график в MathCAD можно не только просмотреть, но и сохранить в виде видеоклипа. Для этого используется кнопка Save As все в том же окошке настройки анимации. Настроить параметры выходного AVI-файла можно с помощью изменения настроек в окне, которое появляется на экране при нажатии кнопки Options… Как построить анимированный график векторного поля, отдельно рассказывать не буду — полагаю, объединив вместе сведения, изложенные в первом и втором разделах этой статьи, вы и сами без особых усилий справитесь с данной задачей. Графики векторных полей — это ведь, по сути, просто одна из разновидностей графиков, с которыми инструмент анимации может работать абсолютно аналогично тому, как он работает с анимацией графиков двумерных функций. Кстати, с графиками поверхностей, которые мы с вами разбирали на протяжении двух предыдущих статей, этот инструмент, конечно же, ничуть не хуже, чем с графиками двумерными.

Подводя итог теме графиков, которую мы с вами довольно-таки подробно рассмотрели (хотя, конечно, можно было бы и еще подробнее, но что поделаешь — нет в мире совершенства!), можно сказать, что MathCAD располагает очень мощными средствами для работы с самыми разными видами графиков. И, что весьма немаловажно, для пользователя работа с графиками не осложнена какими-либо многозначностями или запутанными способами их (графиков) создания. Хотя, конечно, есть программы, которые способны создавать куда как более красивые графики, но зато MathCAD позволяет объединить создание графиков с расчетом функций, которые они изображают — о том, как многие из этих функций (интегралы, производные, пределы, ряды, и прочие интересные вещи) рассчитываются, мы, я так думаю, еще поговорим.

SF, spaceflyer@tut.by