MathCAD — это просто! Часть 7. Графики поверхностей и графики кривых в пространстве

Как говорится, снова здравствуйте. Как вы уже неоднократно имели возможность убедиться, MathCAD — чрезвычайно мощный математический пакет, который позволяет пользователю решать огромное число самых что ни на есть разнообразных задач, с которыми тот только может столкнуться. Однако стоит отметить, что за все нужно платить, а потому многие задачи решаются довольно громоздко — хотя, впрочем, это проблемы не столько MathCAD'а, сколько математического аппарата, который эта программа реализует. Построение трехмерных графиков поверхностей, с которым мы с вами знакомились в предыдущей статье цикла, оказалось не такой уж и сложной задачей — большую часть статьи я, если помните, рассказывал о том, как эти графики можно потом раскрасить, чтобы они максимально удачно смотрелись в отчете, реферате или презентации. Однако сегодня мы с вами займемся более серьезным делом, чем раскрашивание трехмерных графиков — хотя с графиками, и именно трехмерными, все равно продолжим работать. Чем же мы будем заниматься? Думаю, вы сможете сами ответить на этот вопрос, если продолжите чтение данной статьи.

Когда график врет, и что следует делать в таких случаях?

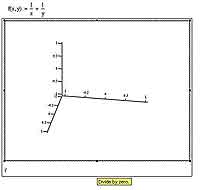Естественно, любой, даже самый точный, график — всего лишь приближенная визуализация некоторой математической функции. Математики даже часто, чтобы это подчеркнуть, говорят не о построении графиков, а об их схематическом изображении. Но, как правило, даже довольно грубого метода построения трехмерных графиков вполне хватает для того, чтобы получить представление о поведении функции в тех или иных областях пространства. На самом деле проблемы, возникающие при построении графиков в MathCAD'е, куда более серьезны и связаны с разрывами функций. Во-первых, MathCAD часто вовсе не захочет строить график тех функций, для которых он найдет неустранимые разрывы в области построения графика. К примеру, попробуйте построить график z = 1/x + 1/y на стандартном для трехмерных графиков интервале от -5 до +5 и посмотрите, что получится. Естественно, вдоль прямых x = 0 и y = 0 график будет уходить в бесконечность. Заранее хочу предупредить, что ничего хорошего получиться не может: неустранимый разрыв на то и неустранимый, что поделать с ним ничего, собственно говоря, попросту невозможно. Поэтому здесь придется как-то изловчаться: искать точку разрыва и строить графики отдельно для областей справа и слева от нее. Если точек разрыва много (например, для периодических функций в знаменателе), то это может оказаться довольно-таки утомительно, но на самом деле какого-либо общего и простого метода решения данной проблемы просто не существует.

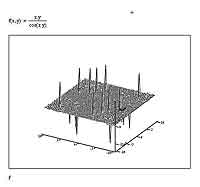Однако на этом напасти с графиками (а точнее, с отображением точек разрыва на них) далеко не заканчиваются — напротив, я бы даже сказал, все только-только начинается. Бывает, что MathCAD вполне успешно (на его собственный взгляд) справляется с такими нехорошими вещами, как разрывы функций. Делает он это, правда, в довольно-таки специфической форме: разрывы эти попросту игнорируются, и их существование на графике никаким образом не отображается. Примером этому может служить построение такого несколько экзотического графика, как z = x*y/cos(x*y). Вполне естественно предположить, что в тех точках, где знаменатель равен нулю (т. е. x*y = pi/2), график будет устремляться к бесконечности. На практике же MathCAD, что называется, "не плюется" на эту функцию, а спокойно строит нечто, что якобы является ее графиком.

Почему такое происходит? В общем-то, секретов нет — нужно только представлять себе, как именно строятся графики в MathCAD'е. Дело в том, что графики MathCAD строит дискретно, вычисляя значения функции в определенных точках, а после соединяя их прямыми. Естественно, чем меньше шаг дискретизации (т.е. расстояние между соседними вычисляемыми значениями функции), тем больше вероятность того, что при построении графика MathCAD столкнется с точкой разрыва — тогда мы получим именно тот самый случай, когда программа откажется напрочь строить такой график. Но бывает и другой случай — как раз такой, который мы сейчас вот здесь с вами рассматривали вторым. Тогда MathCAD просто пропускает точку разрыва, сглаживая ее прямыми — т.е. эта точка попадает между опорными точками, по которым программа строит график нашей поверхности. К сожалению, второй случай проблемы с точками разрыва на практике ничуть не лучше первого (хотя первоначально может показаться, что с ним довольно легко справиться). Если мы уменьшим шаг, с которым MathCAD строит опорные точки графика, то получится как раз первый случай: алгоритм построения графика успешно угодит на точку разрыва и начнет паниковать, подозревая нас в желании заставить его поделить что-нибудь на ноль. Так что, как видите, построение трехмерных графиков — задача, требующая часто творческого подхода к ее решению.

Волшебная функция CreateMesh

Мы с вами уже умеем строить графики поверхностей в трехмерном пространстве, что называется, в лоб. То есть если имеется явная функциональная зависимость координаты z (аппликаты) от x (абсциссы) и y (ординаты). Однако, к сожалению, природа по неведомым ей соображениям не пожелала ограничиться только такими зависимостями — значит, и нам с вами, может так случиться, придется строить график поверхности, заданной не какой-то функцией, а уравнением. К счастью, разработчики MathCAD предусмотрели такую возможность и предложили пользователям функцию, которая будет весьма и весьма полезна при построении подобных пространственных графиков. О ней мы с вами сейчас, конечно же, и поговорим.

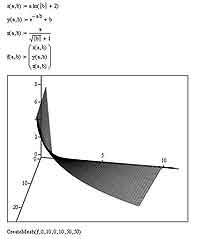Использование функции CreateMesh предполагает параметризацию той поверхности, которую вы хотите визуализировать с использованием MathCAD'а. Поскольку о параметризации я, помнится, не так уж давно рассказывал, думаю, лишний раз подробно останавливаться на том, в чем заключается суть этого процесса, не буду — лучше сразу перейдем к практике использования этой чрезвычайно полезной практически для каждого пользователя функции. Итак, во-первых, нужно задать три функции, описывающие зависимость каждой из координат (x, y, z) от двух параметров. Да, это строгое ограничение: параметров должно быть именно два — с другим числом параметров MathCAD работать не умеет. Правда, стоит отметить, что для построения подавляющего большинства широко распространенных поверхностей этого вполне хватит. Для определенности положим, что параметры у нас будут a и b. После того, как функциональная зависимость задана, функции x(a,b), y(a,b) и z(a,b) нужно сгруппировать в вектор-столбец. Напомню, что для этого нужно создать с помощью кнопки Matrix or Vector, расположенной на панели инструментов Matrix, матрицу размером 3 на 1, в элементы которой и вписать указанные функции. Далее добавляем на рабочую область MathCAD поле трехмерного графика, внизу которого пишем следующее (без кавычек): "CreateMesh(f, 0, 10, 0, 10, 50, 50)". Результаты построение одной из возможных параметрических поверхностей вы можете увидеть на рисунке.

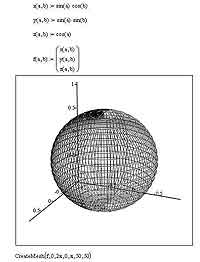Давайте теперь разберемся с параметрами, которые указаны для функции CreateMesh. Каждый из них, как вы наверняка догадываетесь, несет в себе глубокий смысл, а потому менять их местами не представляется возможным. Первым стоит имя нашего вектора с функциями. В принципе, запись, которую вы видите на иллюстрации, можно было бы даже несколько упростить, если бы записать в вектор не x(a,b), y(a,b) и z(a,b), а их непосредственные выражения. Однако я написал все именно в таком виде, чтобы вам было легче понять, что именно где в этом векторе стоит. После имени вектора идут соответственно минимальное и максимальное значения для первого и второго параметров. Здесь у нас границы и для a, и для b принимают, в общем-то, одни и те же значения, но на практике это может быть совершенно не так. Далее идут два параметра, указывающие MathCAD, на сколько шагов разбить указанный диапазон для построения точек, по которым уже будет чертиться собственно график. Все параметры, кроме имени вектора, описывающего поверхность, являются необязательными. И, вообще говоря, есть еще один параметр, который в данном примере опущен — он используется для работы с системами координат, и о нем, я так думаю, мы лучше поговорим как-нибудь в другой раз. Для того, чтобы показать всю простоту и мощь применения CreateMesh, приведу еще один пример, а именно построение с помощью данной функции сферы. Для этого нужно задать следующие уравнения в описанном выше примере: x(a,b) := sin(a)*cos(b); y(a,b) := sin(a)*sin(b); z(a,b) := cos(a). Кроме того, нужно поменять также и диапазоны, в которых будут изменяться a и b: первый параметр будет меняться от нуля до двух пи, второй — от нуля до пи. Результат построения сферы вы также можете увидеть на соответствующем рисунке.

Функция CreateSpace

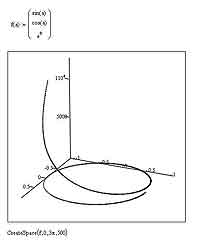Несмотря на все достоинства функции CreateMesh, она не позволяет строить в пространстве отдельных линий, что не есть хорошо. Поэтому для полноты нашего сегодняшнего разговора о разных полезных при построении трехмерных графиков функциях будет неплохо также рассмотреть и такую вещь, как CreateSpace. Фактически эту функцию можно считать аналогом CreateMesh с той лишь разницей (впрочем, оказывающейся довольно существенной), что эту функцию можно использовать для построения кривых в пространстве. Формат записи данных для CreateSpace несколько отличается от аналогичного для CreateMesh. Во-первых, параметр у кривой должен быть только один. Отсюда пляшет и количество параметров у самой функции. Для того, чтобы получить график кривой, а не поверхности, нужно включить в свойствах графика тип Scatter Plot или Data Points; также для удобства просмотра получившихся результатов желательно включить отрисовку не только точек, но и целых линий.

Справедливости ради стоит сказать, что CreateSpace позволяет создавать не только графики кривых, но и графики поверхностей — полагаю, вы уже уловили, что основное отличие этой функции от CreateMesh заключается в том, что она позволяет использовать не два параметра для параметризации поверхности, а только один. Хотя о трехмерных графиках в MathCAD'е мы поговорили уже немало, по-настоящему этот разговор еще только, можно сказать, начинается. Так что готовьте ваши компьютеры к новым интересным вещам, с которыми я вас познакомлю в серии статей "MathCAD — это просто". Ведь действительно же просто, правда?

SF, spaceflyer@tut.by