Flash 8 & Физика. Столкновение точки со стеной
Сегодня мы продолжаем начатый в прошлый раз (см. КГ №14) рассказ о методах интеграции физики во flash. В прошлый раз мы рассмотрели основы векторной математики. Мы узнали, что такое вектор, что такое длина вектора и нормаль к нему и что такое нормализованный вектор. Поняли, как векторы преобразуются в углы, и какой смысл несет скалярное произведение двух векторов. Сегодня мы завершаем рассмотрение этой темы. Нам осталось разобраться с понятием движения по вектору. Также мы рассмотрим механизм определения точки, где два вектора пересекаются. Мы узнали, что вектор задает собой направление движения чего-то. Если вектор состоит из двух компонент (x,y), то это движение на плоскости. Из школьной формулы "расстояние = время * скорость" ясно, что координаты объекта зависят от времени. Во flash есть два стандартных механизма, позволяющих изменять координаты объекта во времени. Прежде всего, если flash основан на понятии временной шкалы, на которой находится множество кадров, сменяющих друг друга, то простейший способ — это ввести код, который срабатывает на событие начала каждого нового кадра. Важно знать, сколько времени занимает один кадр — по умолчанию частота равна 12 кадрам в секунду. Скорость смены кадров определяется настройками документа flash в меню modify -> document.
Для примера создайте любой символ в библиотеке нового документа (я использовал круг, но какой-либо разницы это не имеет). Дайте этому символу имя smb_circle, затем поместите два объекта этого символа на слой Layer1 и дайте им имена obj_circle_1 и obj_circle_2. Введите следующий actionscript код в первом кадре документа.
var v_coords = {start: {x: 10, y: 20}, ort: {x: 0.31, y: 0.94} };
_root.obj_circle_1._x = v_coords.start.x;
_root.obj_circle_1._y = v_coords.start.y;
var count_frames = 0;
// счетчик количества пройденных кадров
_root.onEnterFrame = function (){
count_frames ++;
_root.obj_circle_1._x += v_coords.ort.x * 10;
_root.obj_circle_1._y += v_coords.ort.y * 10;
// или так
_root.obj_circle_2._x = 200+ v_coords.start.x + v_coords.ort.x * 10 * count_frames;
_root.obj_circle_2._y = v_coords.start.y + v_coords.ort.y * 10 * count_frames;
}
Как видите, при запуске ролика падение двух шариков абсолютно идентично, просто второй падает на 200 px правее. Я создал вектор v_coords, задающий начальные координаты шарика, а затем назначил функцию — обработчик события onEnterFrame (при наступлении каждого очередного кадра, т.е. каждую 12 долю секунды), который изменяет значения координат объекта obj_circle на величину произведения соответствующей компоненты нормализованного вектора и числа десяти. Почему я использовал произведение 10, и именно нормализованного вектора. Да просто это смотрится неплохо: шарик медленно ползет сверху вниз — не более того. На самом деле, нужно понимать, что в то время как на экране мы оперируем пикселями, объекты окружающего нас мира задаются в других единицах измерения, и все, что вам нужно — так это задать правила соотношения этих величин. Это достаточно нетривиальная задача — иногда в целях геймплея приходится нарушать эти пропорции. Часть игр, если их делать действительно похожими на реальную жизнь, будут невообразимо скучны или, наоборот, требовать от игрока просто нечеловеческой реакции или усидчивости. В общем, играйтесь коэффициентами, но оставьте базовые законы математики и физики в покое. А теперь отложим в сторону философию и рассмотрим чисто технические сложности подхода, основанного на onEnterFrame. Flash построен на концепции кадров, сменяющихся друг за дружкой. Если вы указываете в свойствах документа некоторую частоту FPS, то это значит, что flash просто будет пытаться поддерживать именно такую скорость выполнения. Но это не означает, что он действительно может выполнить вашу просьбу. На это влияют такие факторы, как загрузка процессора иными задачами, браузером, антивирусом. Возможно, что объем вычислений будет разниться в разных кадрах, а, следовательно, заявленные 12 кадров в секунду могут упасть до меньших значений. Давайте попробуем другой подход, основанный на таймере. Мы можем попросить flash извещать нас каждые, скажем, 100 миллисекунд и выполнять действия по расписанию. Для этого нам следует воспользоваться функцией setInterval. В простейшем случае в качестве параметров этой функции следует указать имя функции, которая будет вызываться по расписанию, затем — значение интервала в миллисекундах, и, наконец, можно передать произвольное количество параметров, которые будут, в свою очередь, переданы функции, вызываемой из таймера. Для демонстрации некоторых неприятных моментов, связанных с реализацией setInterval, давайте модифицируем пример выше.
var v_coords = {start: {x: 10, y: 20}, ort: {x: 0.31, y: 0.94} };
_root.obj_circle_1._x = v_coords.start.x;
_root.obj_circle_1._y = v_coords.start.y;
_root.obj_circle_2._x = 200+ v_coords.start.x;
_root.obj_circle_2._y = v_coords.start.y;
var initialTime_1 = getTimer();
var initialTime_2 = getTimer();
_root.onEnterFrame = function (){
var nowTime = getTimer();
_root.obj_circle_1._x += v_coords.ort.x * 1;
_root.obj_circle_1._y += v_coords.ort.y * 1;
trace ("-- onEnterFrame "+ (nowTime — initialTime_1));
initialTime_1 = getTimer();
}
// функция, выполняющая изменение координат мяча
// параметры _fio, _age, _sex не используются и служат только
// для демонстрации
function fooUpdateBall (_fio, _age, _sex){
var nowTime = getTimer();
_root.obj_circle_2._x += v_coords.ort.x * 1;
_root.obj_circle_2._y += v_coords.ort.y * 1;
trace ("-- setInteral "+ (nowTime — initialTime_2));
initialTime_2 = getTimer();
updateAfterEvent ();
}
// запускаем функцию, срабатывающую каждые 50 мс
setInterval (fooUpdateBall, 50, "Bill", 12, "male");
Для оценки времени я использовал функцию getTimer, которая возвращает величину количества времени, прошедшего с момента запуска ролика. Для удобства я изменил значение частоты кадров до 20 кадров в секунду, или, что то же самое, 50 миллисекунд между отдельными кадрами (именно это число указано вторым параметром функции setInterval). Предположительно два шарика должны двигаться синхронно. Давайте проверим и запустим пример. А вот и нет. Шарики движутся хоть и близко, но не с одинаковой скоростью. Более того, обратите внимание на значения, выводимые функцией trace — разность времени скачет от 45 миллисекунд до 55, и иногда в вызовах setInterval разницы подскакивают до 100 миллисекунд. Теперь изменим параметр "время задержки" с 50 до 60 миллисекунд и соберем статистику (время задержки подскочило до 100 и не опускается ниже), теперь уменьшим время до 10 и снова соберем статистику (здесь числа примерно равны 15). Проще говоря, если вы просите flash вызвать некоторую функцию через определенный интервал, то будьте готовы к погрешности, примерно равной величине времени для одного кадра. С другой стороны, уменьшать время кадра до величин, скажем, 60 кадров в секунду также нельзя, чтобы не привести к катастрофической потере производительности. Нельзя сказать, что недостаток погрешностей характерен только для flash — схожими проблемами страдают любые приложения, ведь в основе лежит квантование времени средствами операционной системы и многозадачность. Единственный выход — смириться и пытаться вести учет времени самим. Так, если вашу функцию вызвали по расписанию, не стоит верить, что это произошло точно через 50 миллисекунд — просто узнайте разницу во времени между прошедшим и текущим вызовом и пользуйтесь школьной формулой S=V*T. Примерно как в примере ниже, хотя там также возникают погрешности, но это лучшее, что можно предложить:
var initialTime_2= getTimer();
function fooUpdateBall (_fio, _age, _sex){
var nowTime = getTimer();
var time: Number = int(( nowTime — initialTime_2) / 60) ;
_root.obj_circle_2._x = 200+ v_coords.start.x + v_coords.ort.x * time;
_root.obj_circle_2._y = v_coords.start.y + v_coords.ort.y * time;
updateAfterEvent ();
}
// обратите внимание на число 60 здесь и на то, что внутри функции fooUpdateBall разницу во времени я делю на него же
setInterval (fooUpdateBall, 60, "Bill", 12, "male");
Да, еще. Напишите письмо adobe, чтобы они наконец-то озаботились поддержкой в flash player многопоточных вычислений, синхронизации и заодно многоядерных машин. А ведь еще есть проблема, связанная с лимитом времени выполнения одного кадра в 15 секунд, и если ваш код сложнее, то крутитесь, как хотите. И последняя рекомендация: в приведенных выше примерах расчет новых значений _x, _y был тривиален — возможно, что в иной ситуации расчет будет требовать условных конструкций, циклов — проще говоря, нужны будут промежуточные вычисления для определения новых координат объекта клипа. Никогда, никогда не используйте для сохранения этих промежуточных значений переменные _x, _y. Как только вы присваиваете новые значения этим переменным, то flash тут же пытается переместить объект в промежуточную точку — только затем, чтобы через долю секунды еще переместить его уже в конечную точку. Теперь разберемся с пересечением объектов. Итак, у нас есть вектор движения материальной точки, и есть вектор, задающий прямую. Необходимо узнать, пересекутся ли они, и если да, то в какой точке. Если два вектора параллельны (т.е. равны направления их движения), то они не пересекаются. Внимание! Я не говорю: "направлены в одну сторону".
// функция, выполняющая проверку параллельности двух векторов
function parallel(vec1, vec2){
return (((vec1.ort.x == vec2.ort.x) and (vec1.ort.y == vec2.ort.y))
or ((vec1.ort.x == -vec2.ort.x) and (vec1.ort.y == -vec2.ort.y)));
}
var vec1 = {start: {x: 10, y: 10}, ort: {x: 0.31, y: 0.94} };
var vec2 = {start: {x: 200, y: 40}, ort: {x: -0.31, y: -0.94} };
// функция, рисующая два вектора для иллюстрации
function drawVector(v, c){
_root.lineStyle(5, c, 100, true, "none", "round", "miter", 1);
_root.moveTo (v.start.x, v.start.y);
_root.lineTo (v.start.x + v.ort.x* 500, v.start.y + v.ort.y*500);
}
// рисуем вектора разными цветами
drawVector (vec1, 0xff00ff);
drawVector (vec2, 0xffff00);
// и проверяем их на пересечение
if (parallel (vec1, vec2))
trace ("parallel");
else
trace ("intersection");
После проверки того, что пересечение между двумя векторами v1 и v2 возможно, остается определить только координаты этой точки. Алгоритм вкратце таков: мы находим новый вектор vec3, который соединяет начало v1 и начало v2. Затем делим между собой скалярное произведение нормали vec3 и vec2 на скалярное произведение нормали vec1 и vec2. Получившееся число задает, насколько далеко в направлении вектора vec1 находится точка пересечения. Если формула вам непонятна, то вы можете пойти альтернативным путем. Например, вы знаете, что по двум точкам вектора (начальной и конечной) возможно задать уравнение, определяющее множество точек, лежащих на прямой (x2-x)(y2-y1)-(y2-y)(x2-x1) = 0. С другой стороны точка пересечения принадлежит обоим векторам, а значит, надо просто решить систему из двух уравнений.
x(y1-y2)+y(x2-x1)+(x1*y2 — x2*y1) = 0
x(b1-b2)+y(a2-a1)+(a1*b2 — a2*b1) = 0
Или, что то же самое, если спрятать формулы под новыми обозначениями:
x*A1+y*B1+C1=0 и x*A2+y*B2+C2=0
Решать уравнения с двумя неизвестными нас всех учили еще в школе. Так что дерзайте.
// создаем два вектора
var vec2 = {start: {x: 0, y: 0}, delta: {x: 10, y: 5} };
var vec3 = {start: {x: 5, y: 0}, delta: {x: 0, y: 5} };
// вычисляем их длины
vec2.len = Math.sqrt(vec2.delta.x*vec2.delta.x + vec2.delta.y*vec2.delta.y);
vec3.len = Math.sqrt(vec3.delta.x*vec3.delta.x + vec3.delta.y*vec3.delta.y);
// вычисляем нормализованные векторы
vec2.ort = {x: vec2.delta.x / vec2.len, y: vec2.delta.y / vec2.len};
vec3.ort = {x: vec3.delta.x / vec3.len, y: vec3.delta.y / vec3.len};
// рисуем векторы
drawVector(vec1,0xff00ff);
drawVector(vec2,0xffff00);
// функция, находящая пересечение двух векторов
function intersection(v1, v2) {
var v3 = {start: {x: v1.x, y: v1.y},
delta: {x: v2.start.x-v1.start.x, y:v2.start.y-v1.start.y}};
// проверяем два вектора на параллельность
if (parallel(v1, v2)) {
// и если они действительно параллельны, то возвращаем особое значение
return {status: false}
}else var t = scalarNV(v3, v2) / scalarNV(v1, v2);
return {status: true, x: v1.start.x+v1.delta.x*t, y: v1.start.y+v1.delta.y*t};
}
// произведение нормали первого вектора и второго
function scalarNV(v1, v2) {
return v1.delta.x*v2.delta.y-v1.delta.y*v2.delta.x;
}
var vi = intersection (vec3,vec2 );
// в поле "статус возвращенного объекта" хранится признак того, было ли пересечение
if (vi.status)
// и если да — пересечение было, то выводим его координаты
trace ('intersection was at ' + vi.x + ", " + vi.y);
else
trace ('vectors are parallels');
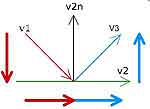
Теперь рассмотрим, как определить новый вектор движения точки после удара о стену. Рассмотрите рис. 1 (на нем обозначены v1 — вектор движения точки до удара о стену, v2 — вектор стены, v2n — нормаль стены и v3 — вектор отраженной точки; также смотрите на проекции векторов до и после удара) и обратите внимание на проекции векторов движения точки до и после удара на нормаль стены и вектор самой стены. План действий вкратце таков: найти точку пересечения вектора стены и вектора движения точки — возможно, они вообще не пересекаются, тогда нам ничего делать не нужно. Если же пересечение все-таки было, то нужно найти нормаль стены — как это сделать, смотри в прошлой части статьи; затем нужно спроецировать вектор движения точки v1 на вектор стены v2 и на его нормаль v2n. Затем получившуюся проекцию на нормаль мы перевернем (перевернем обе компоненты, как x, так и y — рисунок показывает ситуацию падения на горизонтальную плоскость, мы же выводим универсальную формулу для произвольно ориентированной стены). И последний шаг: нужно на основании полученных проекций (в том числе и перевернутой) сформировать новый вектор, который будет равен сумме этих проекций, и исходить из точки, найденной с помощью алгоритма поиска пересечения.
// код функций scalarNV, intersection берем из предыдущего примера
function len (v){
return Math.sqrt(v.delta.x*v.delta.x + v.delta.y*v.delta.y);
}
// обновленная функция, рисующая два вектора для иллюстрации
function drawVector(v, c){
_root.lineStyle(5, c, 100, true, "none", "round", "miter", 1);
_root.moveTo (v.start.x, v.start.y);
_root.lineTo (v.start.x + v.delta.x, v.start.y + v.delta.y);
}
// функция, находящая скалярное произведение двух векторов
function dot (v1, v2){
return v1.delta.x*v2.delta.x + v1.delta.y * v2.delta.y;}
// функция, выполняющая расчет отражения точки от стены
function makeBounce (){
// очищаем сцену от ранее нарисованных объектов
_root.clear();
// создаем два вектора
var v1 = {start: {x: 100, y: 100}, delta: {x: 100, y: 300} };
// v1 — задает направление падения точки
var v2 = {start: {x: 10, y: 300}, delta: {x: 400, y: 200} };
// случайным образом изменяем направление движения падающей точки
v1.delta.x += (0.5 — Math.random())*500;
v1.delta.y += (0.5 — Math.random())*500;
// v2 — задает стену
// выполним подготовительные операции для векторов — вычисляем их длины
v1.len = len(v1)
v2.len = len(v2)
// вычисляем нормализованные векторы
v1.ort = {x: v1.delta.x / v1.len,y: v1.delta.y / v1.len};
v2.ort = {x: v2.delta.x / v2.len,y: v2.delta.y / v2.len};
// рисуем векторы
drawVector(v1,0xff00ff);
drawVector(v2,0xffff00);
var vi = intersection (v1,v2 );
if (vi.status){
// и если пересечение было, то выводим его координаты
trace ('intersection was at ' + vi.x + ", " + vi.y);
// находим левую нормаль к вектору стены
v2.left = {delta: {x: v2.delta.y, y: — v2.delta.x } };
// находим длину нормали вектора стены — вообще-то она должна быть равна длине исходного вектора стены v2
v2.left.len = len (v2.left);
// находим нормализованный вектор левой нормали стены
v2.left.ort = {x: v2.left.delta.x / v2.left.len,y: v2.left.delta.y / v2.left.len};
// находим скалярные произведения — они нужны для расчета проекций векторов
var dot_v1_v2 = dot (v1, v2);
var dot_v1_v2left = dot (v1, v2.left);
// теперь сами проекции
var projectV2 = {delta: {x: dot_v1_v2*v2.ort.x/(v2.len), y: dot_v1_v2*v2.ort.y/v2.len} };
var projectV2left = {delta: {x: dot_v1_v2left*v2.left.ort.x/v2.left.len, y: dot_v1_v2left*v2.left.ort.y/v2.left.len} };
// переворачиваем проекцию на нормаль стены
projectV2left.delta.x *= -1;
projectV2left.delta.y *= -1;
// и, наконец, складываем две проекции вектора, получая исходящий вектор движения отраженной точки
var v3 = {delta: {x: projectV2.delta.x + projectV2left.delta.x, y: projectV2.delta.y + projectV2left.delta.y} };
// теперь, зная направление движения вектора, необходимо задать его начальную точку
// это будет точка пересечения
v3.start = vi;
// проверяем, чтобы длина входного вектора была равна длине исходящего вектора,
// если у вас эти цифры не совпали, то где-то находится ошибка
trace (len(v3)+ ", "+ len(v1));
drawVector(v3,0x00ffff);
}
else
trace ('vectors are parallels');
}
// запускаем таймер многократного повторения имитации столкновения
setInterval (makeBounce, 2000);
На сегодня все. В следующий раз мы разберем поведение более сложных объектов, чем точка и линия.
black zorro, black-zorro@tut.by
Для примера создайте любой символ в библиотеке нового документа (я использовал круг, но какой-либо разницы это не имеет). Дайте этому символу имя smb_circle, затем поместите два объекта этого символа на слой Layer1 и дайте им имена obj_circle_1 и obj_circle_2. Введите следующий actionscript код в первом кадре документа.
var v_coords = {start: {x: 10, y: 20}, ort: {x: 0.31, y: 0.94} };
_root.obj_circle_1._x = v_coords.start.x;
_root.obj_circle_1._y = v_coords.start.y;
var count_frames = 0;
// счетчик количества пройденных кадров
_root.onEnterFrame = function (){
count_frames ++;
_root.obj_circle_1._x += v_coords.ort.x * 10;
_root.obj_circle_1._y += v_coords.ort.y * 10;
// или так
_root.obj_circle_2._x = 200+ v_coords.start.x + v_coords.ort.x * 10 * count_frames;
_root.obj_circle_2._y = v_coords.start.y + v_coords.ort.y * 10 * count_frames;
}
var v_coords = {start: {x: 10, y: 20}, ort: {x: 0.31, y: 0.94} };
_root.obj_circle_1._x = v_coords.start.x;
_root.obj_circle_1._y = v_coords.start.y;
_root.obj_circle_2._x = 200+ v_coords.start.x;
_root.obj_circle_2._y = v_coords.start.y;
var initialTime_1 = getTimer();
var initialTime_2 = getTimer();
_root.onEnterFrame = function (){
var nowTime = getTimer();
_root.obj_circle_1._x += v_coords.ort.x * 1;
_root.obj_circle_1._y += v_coords.ort.y * 1;
trace ("-- onEnterFrame "+ (nowTime — initialTime_1));
initialTime_1 = getTimer();
}
// функция, выполняющая изменение координат мяча
// параметры _fio, _age, _sex не используются и служат только
// для демонстрации
function fooUpdateBall (_fio, _age, _sex){
var nowTime = getTimer();
_root.obj_circle_2._x += v_coords.ort.x * 1;
_root.obj_circle_2._y += v_coords.ort.y * 1;
trace ("-- setInteral "+ (nowTime — initialTime_2));
initialTime_2 = getTimer();
updateAfterEvent ();
}
// запускаем функцию, срабатывающую каждые 50 мс
setInterval (fooUpdateBall, 50, "Bill", 12, "male");
var initialTime_2= getTimer();
function fooUpdateBall (_fio, _age, _sex){
var nowTime = getTimer();
var time: Number = int(( nowTime — initialTime_2) / 60) ;
_root.obj_circle_2._x = 200+ v_coords.start.x + v_coords.ort.x * time;
_root.obj_circle_2._y = v_coords.start.y + v_coords.ort.y * time;
updateAfterEvent ();
}
// обратите внимание на число 60 здесь и на то, что внутри функции fooUpdateBall разницу во времени я делю на него же
setInterval (fooUpdateBall, 60, "Bill", 12, "male");
Да, еще. Напишите письмо adobe, чтобы они наконец-то озаботились поддержкой в flash player многопоточных вычислений, синхронизации и заодно многоядерных машин. А ведь еще есть проблема, связанная с лимитом времени выполнения одного кадра в 15 секунд, и если ваш код сложнее, то крутитесь, как хотите. И последняя рекомендация: в приведенных выше примерах расчет новых значений _x, _y был тривиален — возможно, что в иной ситуации расчет будет требовать условных конструкций, циклов — проще говоря, нужны будут промежуточные вычисления для определения новых координат объекта клипа. Никогда, никогда не используйте для сохранения этих промежуточных значений переменные _x, _y. Как только вы присваиваете новые значения этим переменным, то flash тут же пытается переместить объект в промежуточную точку — только затем, чтобы через долю секунды еще переместить его уже в конечную точку. Теперь разберемся с пересечением объектов. Итак, у нас есть вектор движения материальной точки, и есть вектор, задающий прямую. Необходимо узнать, пересекутся ли они, и если да, то в какой точке. Если два вектора параллельны (т.е. равны направления их движения), то они не пересекаются. Внимание! Я не говорю: "направлены в одну сторону".
// функция, выполняющая проверку параллельности двух векторов
function parallel(vec1, vec2){
return (((vec1.ort.x == vec2.ort.x) and (vec1.ort.y == vec2.ort.y))
or ((vec1.ort.x == -vec2.ort.x) and (vec1.ort.y == -vec2.ort.y)));
}
var vec1 = {start: {x: 10, y: 10}, ort: {x: 0.31, y: 0.94} };
var vec2 = {start: {x: 200, y: 40}, ort: {x: -0.31, y: -0.94} };
// функция, рисующая два вектора для иллюстрации
function drawVector(v, c){
_root.lineStyle(5, c, 100, true, "none", "round", "miter", 1);
_root.moveTo (v.start.x, v.start.y);
_root.lineTo (v.start.x + v.ort.x* 500, v.start.y + v.ort.y*500);
}
// рисуем вектора разными цветами
drawVector (vec1, 0xff00ff);
drawVector (vec2, 0xffff00);
// и проверяем их на пересечение
if (parallel (vec1, vec2))
trace ("parallel");
else
trace ("intersection");
После проверки того, что пересечение между двумя векторами v1 и v2 возможно, остается определить только координаты этой точки. Алгоритм вкратце таков: мы находим новый вектор vec3, который соединяет начало v1 и начало v2. Затем делим между собой скалярное произведение нормали vec3 и vec2 на скалярное произведение нормали vec1 и vec2. Получившееся число задает, насколько далеко в направлении вектора vec1 находится точка пересечения. Если формула вам непонятна, то вы можете пойти альтернативным путем. Например, вы знаете, что по двум точкам вектора (начальной и конечной) возможно задать уравнение, определяющее множество точек, лежащих на прямой (x2-x)(y2-y1)-(y2-y)(x2-x1) = 0. С другой стороны точка пересечения принадлежит обоим векторам, а значит, надо просто решить систему из двух уравнений.
x(y1-y2)+y(x2-x1)+(x1*y2 — x2*y1) = 0
x(b1-b2)+y(a2-a1)+(a1*b2 — a2*b1) = 0
Или, что то же самое, если спрятать формулы под новыми обозначениями:
x*A1+y*B1+C1=0 и x*A2+y*B2+C2=0
Решать уравнения с двумя неизвестными нас всех учили еще в школе. Так что дерзайте.
// создаем два вектора
var vec2 = {start: {x: 0, y: 0}, delta: {x: 10, y: 5} };
var vec3 = {start: {x: 5, y: 0}, delta: {x: 0, y: 5} };
// вычисляем их длины
vec2.len = Math.sqrt(vec2.delta.x*vec2.delta.x + vec2.delta.y*vec2.delta.y);
vec3.len = Math.sqrt(vec3.delta.x*vec3.delta.x + vec3.delta.y*vec3.delta.y);
// вычисляем нормализованные векторы
vec2.ort = {x: vec2.delta.x / vec2.len, y: vec2.delta.y / vec2.len};
vec3.ort = {x: vec3.delta.x / vec3.len, y: vec3.delta.y / vec3.len};
// рисуем векторы
drawVector(vec1,0xff00ff);
drawVector(vec2,0xffff00);
// функция, находящая пересечение двух векторов
function intersection(v1, v2) {
var v3 = {start: {x: v1.x, y: v1.y},
delta: {x: v2.start.x-v1.start.x, y:v2.start.y-v1.start.y}};
// проверяем два вектора на параллельность
if (parallel(v1, v2)) {
// и если они действительно параллельны, то возвращаем особое значение
return {status: false}
}else var t = scalarNV(v3, v2) / scalarNV(v1, v2);
return {status: true, x: v1.start.x+v1.delta.x*t, y: v1.start.y+v1.delta.y*t};
}
// произведение нормали первого вектора и второго
function scalarNV(v1, v2) {
return v1.delta.x*v2.delta.y-v1.delta.y*v2.delta.x;
}
var vi = intersection (vec3,vec2 );
// в поле "статус возвращенного объекта" хранится признак того, было ли пересечение
if (vi.status)
// и если да — пересечение было, то выводим его координаты
trace ('intersection was at ' + vi.x + ", " + vi.y);
else
trace ('vectors are parallels');
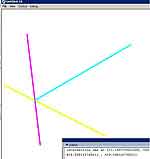
Теперь рассмотрим, как определить новый вектор движения точки после удара о стену. Рассмотрите рис. 1 (на нем обозначены v1 — вектор движения точки до удара о стену, v2 — вектор стены, v2n — нормаль стены и v3 — вектор отраженной точки; также смотрите на проекции векторов до и после удара) и обратите внимание на проекции векторов движения точки до и после удара на нормаль стены и вектор самой стены. План действий вкратце таков: найти точку пересечения вектора стены и вектора движения точки — возможно, они вообще не пересекаются, тогда нам ничего делать не нужно. Если же пересечение все-таки было, то нужно найти нормаль стены — как это сделать, смотри в прошлой части статьи; затем нужно спроецировать вектор движения точки v1 на вектор стены v2 и на его нормаль v2n. Затем получившуюся проекцию на нормаль мы перевернем (перевернем обе компоненты, как x, так и y — рисунок показывает ситуацию падения на горизонтальную плоскость, мы же выводим универсальную формулу для произвольно ориентированной стены). И последний шаг: нужно на основании полученных проекций (в том числе и перевернутой) сформировать новый вектор, который будет равен сумме этих проекций, и исходить из точки, найденной с помощью алгоритма поиска пересечения.
// код функций scalarNV, intersection берем из предыдущего примера
function len (v){
return Math.sqrt(v.delta.x*v.delta.x + v.delta.y*v.delta.y);
}
// обновленная функция, рисующая два вектора для иллюстрации
function drawVector(v, c){
_root.lineStyle(5, c, 100, true, "none", "round", "miter", 1);
_root.moveTo (v.start.x, v.start.y);
_root.lineTo (v.start.x + v.delta.x, v.start.y + v.delta.y);
}
// функция, находящая скалярное произведение двух векторов
function dot (v1, v2){
return v1.delta.x*v2.delta.x + v1.delta.y * v2.delta.y;}
// функция, выполняющая расчет отражения точки от стены
function makeBounce (){
// очищаем сцену от ранее нарисованных объектов
_root.clear();
// создаем два вектора
var v1 = {start: {x: 100, y: 100}, delta: {x: 100, y: 300} };
// v1 — задает направление падения точки
var v2 = {start: {x: 10, y: 300}, delta: {x: 400, y: 200} };
// случайным образом изменяем направление движения падающей точки
v1.delta.x += (0.5 — Math.random())*500;
v1.delta.y += (0.5 — Math.random())*500;
// v2 — задает стену
// выполним подготовительные операции для векторов — вычисляем их длины
v1.len = len(v1)
v2.len = len(v2)
// вычисляем нормализованные векторы
v1.ort = {x: v1.delta.x / v1.len,y: v1.delta.y / v1.len};
v2.ort = {x: v2.delta.x / v2.len,y: v2.delta.y / v2.len};
// рисуем векторы
drawVector(v1,0xff00ff);
drawVector(v2,0xffff00);
var vi = intersection (v1,v2 );
if (vi.status){
// и если пересечение было, то выводим его координаты
trace ('intersection was at ' + vi.x + ", " + vi.y);
// находим левую нормаль к вектору стены
v2.left = {delta: {x: v2.delta.y, y: — v2.delta.x } };
// находим длину нормали вектора стены — вообще-то она должна быть равна длине исходного вектора стены v2
v2.left.len = len (v2.left);
// находим нормализованный вектор левой нормали стены
v2.left.ort = {x: v2.left.delta.x / v2.left.len,y: v2.left.delta.y / v2.left.len};
// находим скалярные произведения — они нужны для расчета проекций векторов
var dot_v1_v2 = dot (v1, v2);
var dot_v1_v2left = dot (v1, v2.left);
// теперь сами проекции
var projectV2 = {delta: {x: dot_v1_v2*v2.ort.x/(v2.len), y: dot_v1_v2*v2.ort.y/v2.len} };
var projectV2left = {delta: {x: dot_v1_v2left*v2.left.ort.x/v2.left.len, y: dot_v1_v2left*v2.left.ort.y/v2.left.len} };
// переворачиваем проекцию на нормаль стены
projectV2left.delta.x *= -1;
projectV2left.delta.y *= -1;
// и, наконец, складываем две проекции вектора, получая исходящий вектор движения отраженной точки
var v3 = {delta: {x: projectV2.delta.x + projectV2left.delta.x, y: projectV2.delta.y + projectV2left.delta.y} };
// теперь, зная направление движения вектора, необходимо задать его начальную точку
// это будет точка пересечения
v3.start = vi;
// проверяем, чтобы длина входного вектора была равна длине исходящего вектора,
// если у вас эти цифры не совпали, то где-то находится ошибка
trace (len(v3)+ ", "+ len(v1));
drawVector(v3,0x00ffff);
}
else
trace ('vectors are parallels');
}
// запускаем таймер многократного повторения имитации столкновения
setInterval (makeBounce, 2000);
На сегодня все. В следующий раз мы разберем поведение более сложных объектов, чем точка и линия.
black zorro, black-zorro@tut.by
Компьютерная газета. Статья была опубликована в номере 16 за 2007 год в рубрике программирование
