Неформальное введение в конечные автоматы: пишем свой калькулятор на Perl
Тем, кто часто пользуется стандартным калькулятором Windows, не раз, вероятно, хотелось закрыть его и сдуть пыль с его старого аппаратного собрата. Намного проще было бы записать все действия, как в школьной тетради, в командной строке и получить результат. В UNIX-системах есть утилита dc, которая работает подобным образом. Но если в Windows подобной нет, что нам мешает написать ее? Эта статья не только для поклонников Perl и любителей все переиначивать (что, в сущности, одно и то же), но и для всех, кто ищет нестандартные подходы к решению задач. Однако целью данной статьи является не калькулятор как таковой (хотя вещь, несомненно, полезная), а демонстрация мощи конечных автоматов при разработке. Калькулятор будет выполнять четыре арифметических действия, но никто не мешает превратить его из школьного в инженерный.
Сначала собственно о конечных автоматах. Здесь необходимо дать минимум сведений тем, кто с ними не знаком: немного теории необходимо для того, чтобы разобраться в коде и начать писать автоматные программы. Язык Perl выбран совсем не случайно (люблю я его:)), а код будет сопровожден подробными комментариями и позволит разобраться в работе программы, так что читатель сможет написать свой конечный автомат на любимом языке. Итак… Определение конечного автомата варьируется от источника к источнику, но для программиста важным является только одно: конечный автомат — это структура данных, и обращаться с ним должно именно как со структурой (при том, что здесь мы никоим образом не затрагиваем объектноориентированные возможности языка Perl во избежание излишней загроможденности кода и для улучшения удобочитаемости текста программы). Поэтому примем следующее определение: Конечным автоматом (далее по тексту КА) называется структура <S, X, F, s0, f>, где:
S — множество состояний;
Х — множество входов;
F — допускающее состояние;
s0 — начальное состояние;
f — функция переходов, определяемая как SxX=S.
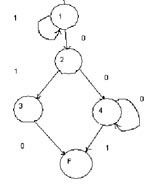
Рис. 1. Пример КА
Рассмотрим граф КА, изображенный на рис. 1. Он имеет следующие состояния: 1 (начальное), 2, 3, 4 и F (допускающее), множество входов — двоичный алфавит (0,1). О его недостатках и возможности оптимизации пока рассуждать не будем. Если наш КА находится в состоянии 1, и мы подаем на его вход единицу, то он как угодно долго будет оставаться в этом состоянии (чем не модель бесконечного цикла?). Как только мы подали на вход 0, он переходит в состояние 2, из которого в другое его переводит уже любой входной сигнал из нашего алфавита (1 — в состояние 3, 0 — в состояние 4). Из этих состояний КА переводят в допускающее состояние F соответственно сигналы 0 и 1. В состоянии F автомат завершает работу. Тогда функцию переходов f можно представить в виде таблицы.
Функция переходов показывает, что данный КА, возможно, нуждается в доработке: например, неясна его реакция на единичный сигнал в состоянии 3. (Но, с другой стороны, мы ведь не знаем назначение этого автомата:)). Но все же этот пример дает некоторое представление о КА. Теперь перейдем непосредственно к реализации нашего КА-калькулятора. Калькулятор получает на вход арифметическое выражение и вычисляет его, предварительно разбивая на токены (атомы). Токеном является либо операнд (число), либо бинарная операция (как уже было сказано, их наш калькулятор знает четыре). Таким образом, наш КА будет иметь следующие состояния:
1. Получение 1-го операнда (процедура state_1()). КА получает первый операнд из входного выражения, разбитого на токены процедурой gettoken().
2. Получение типа бинарной операции (процедура state_2()). Сохраняем тип бинарной операции в глобальной переменной $sign.
3. Получение 2-го операнда (процедура state_3()).
4. Собственно вычисление арифметического выражения с учетом приоритета операций (процедура state_4()).
Последовательный переход КА по этим состояниям дает нам вычисление выражения, состоящего из двух операндов и одной бинарной операции. Для выражения, состоящего из произвольного числа операндов, нам нужно возвратиться из состояния 4 в состояние 1. Граф КА будет иметь вид:
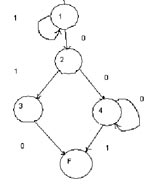
Рис. 2. Граф конечного автомата калькулятора
Символ "эпсилон" при переходе 3-4 означает пустую строку (пустое множество, NULL и т.д.). Наш КА, находясь в состоянии 3, определит второй операнд и совершит безусловный переход в состояние 4, где вычислит выражение. Данный КА не включает обработку ошибок (например, два подряд символа "+", введенных пользователем, или символа, не принадлежащего множеству входного алфавита), но включить данную возможность очень просто — достаточно ввести в граф КА соответствующие состояния и переходы. Таблица функции переходов в этом случае не будет содержать пробелов. Автомат переходит в допускающее состояние из состояния 4 при подаче на вход символа завершения строки. Арифметическое выражение, поданное на вход, уже вычислено и находится в глобальной переменной $res.
 Приведенного выше описания, наверное, достаточно, чтобы привести текст программы целиком. Братья по оружию (читай, по Perl'у), естественно, найдут в ней много возможностей для оптимизации, но тем и хорош Perl!
Приведенного выше описания, наверное, достаточно, чтобы привести текст программы целиком. Братья по оружию (читай, по Perl'у), естественно, найдут в ней много возможностей для оптимизации, но тем и хорош Perl!
#! perl
$op1=$op2=$res=$num=0;#глобальные переменные — сишная привычка, но что делать…
$sign="-";#переменная хранит тип операции
@exp=();#входное арифметическое выражение
@tokens=();#оно же, разбитое на токены
sub gettoken#процедура разбиения входного выражения на токены
{
my @e=@_;
my $tok=0;
my $i;
my $type="pm";
for($i=0;$i<=$#e;$i++)
{
if($e[$i]=~m/[0-9]{1}|\.{1}/s)#используем регулярные выражения Perl
# для выяснения, является ли входной символ числом
{
$tokens[$tok]="b" if $type eq "pm";
$tokens[$tok]="$tokens[$tok]"."$e[$i]";
$tokens[$tok]=~s/b+//;
$type="num";
}
if($e[$i] eq "+" or $e[$i] eq "-" or $e[$i] eq "*" or $e[$i] eq "/") # +,-,*,/
{$type="pm";
$tok++;
$tokens[$tok]=$e[$i];
$tok++;
}
}
}
#следующие четыре процедуры описывают состояния КА
sub state_1
{$op1=$tokens[$num] if $num==0; #получаем 1-й операнд
$op1=$res if $num!=0;
$num++ if $num<=$#tokens;}
sub state_2
{
switch: {
$sign="+",last switch if $tokens[$num] eq "+";#получаем тип бинарной операции
$sign="-",last switch if $tokens[$num] eq "-";
$sign="*",last switch if $tokens[$num] eq "*";
$sign="/",last switch if $tokens[$num] eq "/"
}
$num++ if $num<=$#tokens;
}
sub state_3#получаем 2-й операнд
{$op2=$tokens[$num];
}
sub state_4
{
if($num+1<$#tokens)
{
if($tokens[$num+1] eq "*") #это нужно для учета приоритета операций * и /
{
$op2*=$tokens[$num+2];
$num+=2 if $num<=$#tokens;
state_4();
}
if($tokens[$num+1] eq "/")
{
$op2/=$tokens[$num+2];
$num+=2 if $num<=$#tokens;
state_4();
}
}
$res=$op1+$op2 if $sign eq "+";#предварительно вычисляем выражение
$res=$op1-$op2 if $sign eq "-";
$res=$op1*$op2 if $sign eq "*";
$res=$op1/$op2 if $sign eq "/";
}
#массив содержит ссылки на процедуры состояний
@states=(\&state_1,\&state_2,\&state_3,\&state_4);
#в этой процедуре рекурсивно вычисляется выражение
sub final_automat
{
my $i;
for($i=0;$i<4;$i++)
{&{$states[$i]};} #переходим по состояниям, разыменовывая ссылки
final_automat() if $num<$#tokens;
}
while()
{
print ">>";
@exp=split //,<STDIN>; #подаем выражение на стандартный ввод
gettoken(@exp);
final_automat();
print $res,"\n";
#очищаем все глобальные переменные и массивы для последующего использования
$num=0;
$op1=$op2=$res=0;
@exp=();
@tokens=();
}
Вот, в общем-то, и все. Надеюсь, читателей заинтересовала концепция конечных автоматов. Добавлю только, что мы только прикоснулись к этой модели описания объектов, а ее возможности поистине неисчерпаемы.
Вадим Шандриков
Сначала собственно о конечных автоматах. Здесь необходимо дать минимум сведений тем, кто с ними не знаком: немного теории необходимо для того, чтобы разобраться в коде и начать писать автоматные программы. Язык Perl выбран совсем не случайно (люблю я его:)), а код будет сопровожден подробными комментариями и позволит разобраться в работе программы, так что читатель сможет написать свой конечный автомат на любимом языке. Итак… Определение конечного автомата варьируется от источника к источнику, но для программиста важным является только одно: конечный автомат — это структура данных, и обращаться с ним должно именно как со структурой (при том, что здесь мы никоим образом не затрагиваем объектноориентированные возможности языка Perl во избежание излишней загроможденности кода и для улучшения удобочитаемости текста программы). Поэтому примем следующее определение: Конечным автоматом (далее по тексту КА) называется структура <S, X, F, s0, f>, где:
S — множество состояний;
Х — множество входов;
F — допускающее состояние;
s0 — начальное состояние;
f — функция переходов, определяемая как SxX=S.

Рис. 1. Пример КА
Рассмотрим граф КА, изображенный на рис. 1. Он имеет следующие состояния: 1 (начальное), 2, 3, 4 и F (допускающее), множество входов — двоичный алфавит (0,1). О его недостатках и возможности оптимизации пока рассуждать не будем. Если наш КА находится в состоянии 1, и мы подаем на его вход единицу, то он как угодно долго будет оставаться в этом состоянии (чем не модель бесконечного цикла?). Как только мы подали на вход 0, он переходит в состояние 2, из которого в другое его переводит уже любой входной сигнал из нашего алфавита (1 — в состояние 3, 0 — в состояние 4). Из этих состояний КА переводят в допускающее состояние F соответственно сигналы 0 и 1. В состоянии F автомат завершает работу. Тогда функцию переходов f можно представить в виде таблицы.
| S | X | |
0 | 1 | |
| 1 | 2 | 1 |
| 2 | 4 | 3 |
| 3 | F | - |
| 4 | 4 | F |
Функция переходов показывает, что данный КА, возможно, нуждается в доработке: например, неясна его реакция на единичный сигнал в состоянии 3. (Но, с другой стороны, мы ведь не знаем назначение этого автомата:)). Но все же этот пример дает некоторое представление о КА. Теперь перейдем непосредственно к реализации нашего КА-калькулятора. Калькулятор получает на вход арифметическое выражение и вычисляет его, предварительно разбивая на токены (атомы). Токеном является либо операнд (число), либо бинарная операция (как уже было сказано, их наш калькулятор знает четыре). Таким образом, наш КА будет иметь следующие состояния:
1. Получение 1-го операнда (процедура state_1()). КА получает первый операнд из входного выражения, разбитого на токены процедурой gettoken().
2. Получение типа бинарной операции (процедура state_2()). Сохраняем тип бинарной операции в глобальной переменной $sign.
3. Получение 2-го операнда (процедура state_3()).
4. Собственно вычисление арифметического выражения с учетом приоритета операций (процедура state_4()).
Последовательный переход КА по этим состояниям дает нам вычисление выражения, состоящего из двух операндов и одной бинарной операции. Для выражения, состоящего из произвольного числа операндов, нам нужно возвратиться из состояния 4 в состояние 1. Граф КА будет иметь вид:

Рис. 2. Граф конечного автомата калькулятора
Символ "эпсилон" при переходе 3-4 означает пустую строку (пустое множество, NULL и т.д.). Наш КА, находясь в состоянии 3, определит второй операнд и совершит безусловный переход в состояние 4, где вычислит выражение. Данный КА не включает обработку ошибок (например, два подряд символа "+", введенных пользователем, или символа, не принадлежащего множеству входного алфавита), но включить данную возможность очень просто — достаточно ввести в граф КА соответствующие состояния и переходы. Таблица функции переходов в этом случае не будет содержать пробелов. Автомат переходит в допускающее состояние из состояния 4 при подаче на вход символа завершения строки. Арифметическое выражение, поданное на вход, уже вычислено и находится в глобальной переменной $res.

#! perl
$op1=$op2=$res=$num=0;#глобальные переменные — сишная привычка, но что делать…
$sign="-";#переменная хранит тип операции
@exp=();#входное арифметическое выражение
@tokens=();#оно же, разбитое на токены
sub gettoken#процедура разбиения входного выражения на токены
{
my @e=@_;
my $tok=0;
my $i;
my $type="pm";
for($i=0;$i<=$#e;$i++)
{
if($e[$i]=~m/[0-9]{1}|\.{1}/s)#используем регулярные выражения Perl
# для выяснения, является ли входной символ числом
{
$tokens[$tok]="b" if $type eq "pm";
$tokens[$tok]="$tokens[$tok]"."$e[$i]";
$tokens[$tok]=~s/b+//;
$type="num";
}
if($e[$i] eq "+" or $e[$i] eq "-" or $e[$i] eq "*" or $e[$i] eq "/") # +,-,*,/
{$type="pm";
$tok++;
$tokens[$tok]=$e[$i];
$tok++;
}
}
}
#следующие четыре процедуры описывают состояния КА
sub state_1
{$op1=$tokens[$num] if $num==0; #получаем 1-й операнд
$op1=$res if $num!=0;
$num++ if $num<=$#tokens;}
sub state_2
{
switch: {
$sign="+",last switch if $tokens[$num] eq "+";#получаем тип бинарной операции
$sign="-",last switch if $tokens[$num] eq "-";
$sign="*",last switch if $tokens[$num] eq "*";
$sign="/",last switch if $tokens[$num] eq "/"
}
$num++ if $num<=$#tokens;
}
sub state_3#получаем 2-й операнд
{$op2=$tokens[$num];
}
sub state_4
{
if($num+1<$#tokens)
{
if($tokens[$num+1] eq "*") #это нужно для учета приоритета операций * и /
{
$op2*=$tokens[$num+2];
$num+=2 if $num<=$#tokens;
state_4();
}
if($tokens[$num+1] eq "/")
{
$op2/=$tokens[$num+2];
$num+=2 if $num<=$#tokens;
state_4();
}
}
$res=$op1+$op2 if $sign eq "+";#предварительно вычисляем выражение
$res=$op1-$op2 if $sign eq "-";
$res=$op1*$op2 if $sign eq "*";
$res=$op1/$op2 if $sign eq "/";
}
#массив содержит ссылки на процедуры состояний
@states=(\&state_1,\&state_2,\&state_3,\&state_4);
#в этой процедуре рекурсивно вычисляется выражение
sub final_automat
{
my $i;
for($i=0;$i<4;$i++)
{&{$states[$i]};} #переходим по состояниям, разыменовывая ссылки
final_automat() if $num<$#tokens;
}
while()
{
print ">>";
@exp=split //,<STDIN>; #подаем выражение на стандартный ввод
gettoken(@exp);
final_automat();
print $res,"\n";
#очищаем все глобальные переменные и массивы для последующего использования
$num=0;
$op1=$op2=$res=0;
@exp=();
@tokens=();
}
Вот, в общем-то, и все. Надеюсь, читателей заинтересовала концепция конечных автоматов. Добавлю только, что мы только прикоснулись к этой модели описания объектов, а ее возможности поистине неисчерпаемы.
Вадим Шандриков
Компьютерная газета. Статья была опубликована в номере 46 за 2006 год в рубрике программирование


