О сжатии информации. Спрашивали - отвечаем
В редакцию КГ пришло письмо с вопросами от Сергея Вербило из Барановичей. Сергей написал от имени группы ребят, объединившихся на почве увлечения программированием. Они занялись реализацией алгоритмов статистического сжатия информации, о которых я рассказывал в КГ N№3. Отвечаю с искренним удовольствием!
Первый вопрос затрагивает очень интересную проблему построения оптимального дерева кодирования при сжатии по алгоритму Хаффмана. Действительно, существование такого дерева было упомянуто, но способ его построения не описывался. Нужно сказать, что исследование деревьев является разделом теории графов. В программировании графы служат одной из самых распространенных (и важных) моделей представления данных.
Поэтому, нисколько не претендуя на изложение теории деревьев, воспользуюсь только их свойством так называемой "сбалансированности" и "разбалансированности". Пожалуйста, имейте в виду, что за этими интуитивно понятными и, казалось бы, нестрогими выражениями на деле стоит конкретное математическое содержание.
В примере из КГ n№3 сжималась строка "ААБББВВВВГ". Все встретившиеся в тексте символы были выписаны в порядке убывания частоты их появления: "ВБАГ". Потом было над ними построено двоичное дерево, как это показано на рисунке.
Для того чтобы ярче продемонстрировать сам принцип, я нарисовал максимально разбалансированное дерево. Оно хорошо для случая, когда в исходном тексте встречается не более 9 разных символов. Если основание дерева шире, то для кодирования 9 и 10-го символа потребуется уже по 9 битов. Дальше будет еще хуже, поскольку в сколько-нибудь заслуживающем сжатия файле обязательно, хоть один раз, да встретится каждый из 256 возможных символов.
Другими словами, маловероятно, чтобы выигрыш от более экономного кодирования первых нескольких символов (хотя бы и самых повторяемых) перекрыл потери от роста кода для всех остальных. Впрочем, для каждого конкретного случая это можно точно подсчитать.
А теперь взгляните на рисунок, где изображена другая крайность - полностью сбалансированное дерево. В полностью сбалансированном дереве путь, ведущий к любому из символов, имеет одинаковую длину. Если в основании дерева поместить все 256 символов, то каждому из них будет соответствовать 8-битовый код. То есть коэффициент сжатия окажется равным нулю.
Итак, в крайностях правды нет. Выход в том, чтобы, располагая частотами появления символов в исходном тексте, разбалансировать левую часть дерева и сбалансировать правую. Тогда для самых массовых символов мы получим самые короткие коды, сулящие наивысшую степень сжатия. А редким символам будут поставлены в соответствие длинные коды, но наименьшей возможной длины.
Глубина разбалансировки дерева и его конечный вид очень сильно зависят от распределения частот символов. Как уже упоминалось, алгоритм Хаффмана оптимален для случая, когда частоты символов кратны степеням двойки. Если распределение близко к равномерному, то вместо сжатия можно получить рост закодированного текста. Конечно, можно вначале построить сбалансированное дерево, а потом искать оптимум, шаг за шагом его "облегчая" его левую сторону, но это долгий путь.
К счастью, Хаффман уже предложил простой способ построения оптимального дерева. Вот его описание. Предположим, в исходном тексте встречаются символы от S(0), S(1) ... S(n). Частоты, с которыми они появляются, обозначим F(0), F(1) ... F(n). Для простоты положим, что символы уже отсортированы по убыванию частоты, то есть F(0)>F(1)> ... >F(n). Дерево строится снизу вверх и справа налево. При этом повторяются следующие шаги.
Сначала объединим символы с наименьшими частотами S(n-1) и S(n). Нарисуем над ними ветви "домиком". В результате, вместо двух, у нас появится один комбинированный символ SS с частотой FF=F(n-1)+F(n). SS - это поддерево. В дальнейших событиях оно участвует на правах простого символа. Следует учесть произошедшее изменение в наборе символов. Было: S(0), S(1) ... S(n); стало: S(0), S(1) ... S(n-2), SS. Очевидно, что новый набор нужно заново отсортировать в порядке убывания частоты. После этого опять следует объединить два символа с наименьшими частотами в новый комбинированный символ (поддерево). Описанная процедура повторяется до тех пор, пока есть, что объединять.
Вот какое дерево получится для исходного текста "ААББВВГГГДДДДД". На рисунке комбинированные символы обозначены знаком плюса.
Первый, третий и пятый шаги - объединение, второй и четвертый - сортировка, а на шестом получен результат: частично сбалансированное дерево. Осталось только расставить нолики и единички рядом с его ветвями. Но и без них легко видеть, что символ Д кодируется одним битом, а все остальные символы - тремя.
Второй вопрос, заданный Сергеем, касался способа представления дерева для записи в файл. Все желающие могут попробовать изобрести что-то свое, руководствуясь простым принципом сохранения информации. Применительно к нашему случаю он будет звучать так, что чем больше мы знаем о своем дереве, тем большая часть информации будет содержаться в алгоритме записи и тем короче станет информация, сохраняемая в файл.
Действительно, полностью сбалансированное дерево можно восстановить, зная только число символов, "над" которыми оно было построено. То же самое можно сказать о любом дереве с известной структурой. Для дерева, вид которого нельзя заранее предсказать, я знаю один старый, но безотказный способ. Вполне вероятно, что он не является самым экономичным, зато он прост. Взгляните на следующий рисунок.
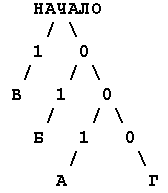
Речь идет о том, чтобы записать путь обхода всех узлов дерева. Сведения о каждом из узлов представляются двумя битами. Узел можно сравнить с перекрестком, а биты - с дорожными указателями. 00 - тупик, 01 - поворот налево, 10 - направо, 11 - в любую сторону. Способ обхода как в лабиринте: идем вперед, сворачивая все время направо, пока не зайдем в тупик. Из тупика возвращаемся до ближайшего перекрестка и сворачиваем на еще не проверенную дорогу, по которой идем вперед, все время сворачивая направо, пока...
Короче говоря, путь обхода дерева, представленного на рисунке, может быть записан битовой строкой 11001111001100111111001100111111. Пожалуй, нет нужды учитывать при записи пути еще и возвраты. Мы ведь и так знаем, что после тупика (00) нужно вернуться к еще непроверенной развилке. С учетом этого запись пути обхода будет выглядеть так: 110011110000110000.
А вот как следует восстанавливать дерево, читая биты попарно. Этот процесс лучше проследить, вооружившись карандашом. 11 - из начала ведут два пути. Наметим их. Согласно нашим правилам, сворачиваем направо, а там 00 - тупик! Возвращаемся, чтобы пройти по намеченному, но еще не проверенному пути. Там 11 - развилка. Наметим пути и пойдем по правому. 11 - опять развилка! Продолжая в том же духе, можно полностью восстановить исходное дерево.
И в завершение разговора о путях обхода двоичных деревьев еще два замечания. Во-первых, если мы абсолютно уверены, что в деревьях, построенных по Хаффману, каждый узел является либо тупиком, либо развилкой, то можно обойтись не двумя, а одним битом. Я не проверял, но это очень похоже на правду. Если так, то запись пути может стать короче в два раза: 101100100.
Во-вторых, есть подозрение, что в любом двоичном дереве для 256 символов - одинаковое количество узлов. Если оно оправдается, то возникнет следующий вопрос: а зависит ли длина пути обхода двоичного дерева от вида дерева? Ведь при записи пути мы просто перечисляем все узлы в определенном порядке и ни один из них не упоминаем дважды. Можете посчитать на досуге...
Про кодирование по Маркову, о котором спрашивал Сергей Вербило, я, увы, ничего рассказать не смогу. Мне практически не приходилось работать с этим разделом высшей математики. А вот просьбу пояснить алгоритм арифметического кодирования по Илиасу исполнить нетрудно. Для начала напомню, что в алгоритме используются не абсолютные частоты символов, а относительные, то есть вероятности их появления в исходном тексте.
При арифметическом кодировании вычисляется число в интервале от 0 до 1. По мере роста числа обработанных исходных символов интервал становится уже и уже, а для записи числа требуется все большее количество битов. Каждый последующий символ уменьшает интервал на величину, обратно пропорциональную вероятности символа. Чем больше вероятность, тем меньше убывание интервала, тем меньше битов добавляется к итоговому числу.
Предположим, в исходном тексте встречаются символы S(0), S(1) ... S(n). Вероятности, с которыми они появляются, обозначим F(0), F(1) ... F(n). Поскольку мы имеем дело с вероятностями, то сумма F(0)+F(1)+ ... +F(n) равна единице. Поставим символу S(0) в соответствие интервал от 0 до F(0), S(1) - от F(0) до F(0)+F(1) и так далее. Графически это можно представить как деление отрезка [0,1] на интервалы длиной F(0), F(1) ... F(n) и надписывание над интервалами соответствующих символов.
Итак, наш рабочий интервал [0,1] и мы подготовились к кодированию первого символа S(i) исходного текста. Как только он будет прочитан, рабочий интервал станет равным [X(i)-F(i), X(i)], где X(i) вычисляется по формуле F(0)+F(1)+ ... +F(i). Чтобы подготовиться к кодированию второго символа S(j), нужно разделить новый интервал в тех же пропорциях, в каких был поделен исходный единичный отрезок.
Если не ошибаюсь, то нижняя граница нового интервала будет равна X(i)+F(i)*(X(j)-F(j)-1), а верхнюю можно получить, прибавив F(i)*F(j) к нижней. Повторяя процесс пропорционального деления интервала для каждого последующего символа, мы, в конце концов, получим окончательный интервал. Любое число, выбранное наугад в данном интервале, обладает весьма примечательным свойством: оно одновременно находится внутри каждого из вычислявшихся по ходу дела интервалов!
Именно это позволяет восстановить исходный текст, если мы знаем распределение вероятностей закодированных символов. Судите сами: делим единичный отрезок пропорционально вероятностям символов и находим, в какой интервал попадает кодовое число. Он и укажет, каков первый символ. Пропорционально делим интервал для найденного символа и опять смотрим, какому символу принадлежит интервал, где оказалось кодовое число. И так далее.
Я уже напоминал об идее алгоритма, но у него есть неожиданное свойство, не до конца укладывающееся в описанную логику. Вы помните: чем уже интервал, тем больше битов требуется... Так вот, если кодовое число внутри интервала выбирать не наугад, а с большим разбором, можно просто невероятно поднять эффективную степень сжатия. Фокус в том, что для записи числа, находящегося внутри даже очень узкого интервала, может потребоваться гораздо меньше битов, чем для представления границ интервала. Если, конечно, повезет найти соответствующее число.
Самый эффектный тому пример - число 0.5, которое, с одной стороны, кодируется всего одним битом, а с другой - может находиться в пределах невероятно узкого интервала, для записи границ которого нужны тысячи или миллионы битов...
Евгений Щербатюк
Первый вопрос затрагивает очень интересную проблему построения оптимального дерева кодирования при сжатии по алгоритму Хаффмана. Действительно, существование такого дерева было упомянуто, но способ его построения не описывался. Нужно сказать, что исследование деревьев является разделом теории графов. В программировании графы служат одной из самых распространенных (и важных) моделей представления данных.
Поэтому, нисколько не претендуя на изложение теории деревьев, воспользуюсь только их свойством так называемой "сбалансированности" и "разбалансированности". Пожалуйста, имейте в виду, что за этими интуитивно понятными и, казалось бы, нестрогими выражениями на деле стоит конкретное математическое содержание.
В примере из КГ n№3 сжималась строка "ААБББВВВВГ". Все встретившиеся в тексте символы были выписаны в порядке убывания частоты их появления: "ВБАГ". Потом было над ними построено двоичное дерево, как это показано на рисунке.
Для того чтобы ярче продемонстрировать сам принцип, я нарисовал максимально разбалансированное дерево. Оно хорошо для случая, когда в исходном тексте встречается не более 9 разных символов. Если основание дерева шире, то для кодирования 9 и 10-го символа потребуется уже по 9 битов. Дальше будет еще хуже, поскольку в сколько-нибудь заслуживающем сжатия файле обязательно, хоть один раз, да встретится каждый из 256 возможных символов.
Другими словами, маловероятно, чтобы выигрыш от более экономного кодирования первых нескольких символов (хотя бы и самых повторяемых) перекрыл потери от роста кода для всех остальных. Впрочем, для каждого конкретного случая это можно точно подсчитать.
А теперь взгляните на рисунок, где изображена другая крайность - полностью сбалансированное дерево. В полностью сбалансированном дереве путь, ведущий к любому из символов, имеет одинаковую длину. Если в основании дерева поместить все 256 символов, то каждому из них будет соответствовать 8-битовый код. То есть коэффициент сжатия окажется равным нулю.
Итак, в крайностях правды нет. Выход в том, чтобы, располагая частотами появления символов в исходном тексте, разбалансировать левую часть дерева и сбалансировать правую. Тогда для самых массовых символов мы получим самые короткие коды, сулящие наивысшую степень сжатия. А редким символам будут поставлены в соответствие длинные коды, но наименьшей возможной длины.
Глубина разбалансировки дерева и его конечный вид очень сильно зависят от распределения частот символов. Как уже упоминалось, алгоритм Хаффмана оптимален для случая, когда частоты символов кратны степеням двойки. Если распределение близко к равномерному, то вместо сжатия можно получить рост закодированного текста. Конечно, можно вначале построить сбалансированное дерево, а потом искать оптимум, шаг за шагом его "облегчая" его левую сторону, но это долгий путь.
К счастью, Хаффман уже предложил простой способ построения оптимального дерева. Вот его описание. Предположим, в исходном тексте встречаются символы от S(0), S(1) ... S(n). Частоты, с которыми они появляются, обозначим F(0), F(1) ... F(n). Для простоты положим, что символы уже отсортированы по убыванию частоты, то есть F(0)>F(1)> ... >F(n). Дерево строится снизу вверх и справа налево. При этом повторяются следующие шаги.
Сначала объединим символы с наименьшими частотами S(n-1) и S(n). Нарисуем над ними ветви "домиком". В результате, вместо двух, у нас появится один комбинированный символ SS с частотой FF=F(n-1)+F(n). SS - это поддерево. В дальнейших событиях оно участвует на правах простого символа. Следует учесть произошедшее изменение в наборе символов. Было: S(0), S(1) ... S(n); стало: S(0), S(1) ... S(n-2), SS. Очевидно, что новый набор нужно заново отсортировать в порядке убывания частоты. После этого опять следует объединить два символа с наименьшими частотами в новый комбинированный символ (поддерево). Описанная процедура повторяется до тех пор, пока есть, что объединять.
Вот какое дерево получится для исходного текста "ААББВВГГГДДДДД". На рисунке комбинированные символы обозначены знаком плюса.
Первый, третий и пятый шаги - объединение, второй и четвертый - сортировка, а на шестом получен результат: частично сбалансированное дерево. Осталось только расставить нолики и единички рядом с его ветвями. Но и без них легко видеть, что символ Д кодируется одним битом, а все остальные символы - тремя.
Второй вопрос, заданный Сергеем, касался способа представления дерева для записи в файл. Все желающие могут попробовать изобрести что-то свое, руководствуясь простым принципом сохранения информации. Применительно к нашему случаю он будет звучать так, что чем больше мы знаем о своем дереве, тем большая часть информации будет содержаться в алгоритме записи и тем короче станет информация, сохраняемая в файл.
Действительно, полностью сбалансированное дерево можно восстановить, зная только число символов, "над" которыми оно было построено. То же самое можно сказать о любом дереве с известной структурой. Для дерева, вид которого нельзя заранее предсказать, я знаю один старый, но безотказный способ. Вполне вероятно, что он не является самым экономичным, зато он прост. Взгляните на следующий рисунок.
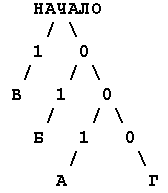
Речь идет о том, чтобы записать путь обхода всех узлов дерева. Сведения о каждом из узлов представляются двумя битами. Узел можно сравнить с перекрестком, а биты - с дорожными указателями. 00 - тупик, 01 - поворот налево, 10 - направо, 11 - в любую сторону. Способ обхода как в лабиринте: идем вперед, сворачивая все время направо, пока не зайдем в тупик. Из тупика возвращаемся до ближайшего перекрестка и сворачиваем на еще не проверенную дорогу, по которой идем вперед, все время сворачивая направо, пока...
Короче говоря, путь обхода дерева, представленного на рисунке, может быть записан битовой строкой 11001111001100111111001100111111. Пожалуй, нет нужды учитывать при записи пути еще и возвраты. Мы ведь и так знаем, что после тупика (00) нужно вернуться к еще непроверенной развилке. С учетом этого запись пути обхода будет выглядеть так: 110011110000110000.
А вот как следует восстанавливать дерево, читая биты попарно. Этот процесс лучше проследить, вооружившись карандашом. 11 - из начала ведут два пути. Наметим их. Согласно нашим правилам, сворачиваем направо, а там 00 - тупик! Возвращаемся, чтобы пройти по намеченному, но еще не проверенному пути. Там 11 - развилка. Наметим пути и пойдем по правому. 11 - опять развилка! Продолжая в том же духе, можно полностью восстановить исходное дерево.
И в завершение разговора о путях обхода двоичных деревьев еще два замечания. Во-первых, если мы абсолютно уверены, что в деревьях, построенных по Хаффману, каждый узел является либо тупиком, либо развилкой, то можно обойтись не двумя, а одним битом. Я не проверял, но это очень похоже на правду. Если так, то запись пути может стать короче в два раза: 101100100.
Во-вторых, есть подозрение, что в любом двоичном дереве для 256 символов - одинаковое количество узлов. Если оно оправдается, то возникнет следующий вопрос: а зависит ли длина пути обхода двоичного дерева от вида дерева? Ведь при записи пути мы просто перечисляем все узлы в определенном порядке и ни один из них не упоминаем дважды. Можете посчитать на досуге...
Про кодирование по Маркову, о котором спрашивал Сергей Вербило, я, увы, ничего рассказать не смогу. Мне практически не приходилось работать с этим разделом высшей математики. А вот просьбу пояснить алгоритм арифметического кодирования по Илиасу исполнить нетрудно. Для начала напомню, что в алгоритме используются не абсолютные частоты символов, а относительные, то есть вероятности их появления в исходном тексте.
При арифметическом кодировании вычисляется число в интервале от 0 до 1. По мере роста числа обработанных исходных символов интервал становится уже и уже, а для записи числа требуется все большее количество битов. Каждый последующий символ уменьшает интервал на величину, обратно пропорциональную вероятности символа. Чем больше вероятность, тем меньше убывание интервала, тем меньше битов добавляется к итоговому числу.
Предположим, в исходном тексте встречаются символы S(0), S(1) ... S(n). Вероятности, с которыми они появляются, обозначим F(0), F(1) ... F(n). Поскольку мы имеем дело с вероятностями, то сумма F(0)+F(1)+ ... +F(n) равна единице. Поставим символу S(0) в соответствие интервал от 0 до F(0), S(1) - от F(0) до F(0)+F(1) и так далее. Графически это можно представить как деление отрезка [0,1] на интервалы длиной F(0), F(1) ... F(n) и надписывание над интервалами соответствующих символов.
Итак, наш рабочий интервал [0,1] и мы подготовились к кодированию первого символа S(i) исходного текста. Как только он будет прочитан, рабочий интервал станет равным [X(i)-F(i), X(i)], где X(i) вычисляется по формуле F(0)+F(1)+ ... +F(i). Чтобы подготовиться к кодированию второго символа S(j), нужно разделить новый интервал в тех же пропорциях, в каких был поделен исходный единичный отрезок.
Если не ошибаюсь, то нижняя граница нового интервала будет равна X(i)+F(i)*(X(j)-F(j)-1), а верхнюю можно получить, прибавив F(i)*F(j) к нижней. Повторяя процесс пропорционального деления интервала для каждого последующего символа, мы, в конце концов, получим окончательный интервал. Любое число, выбранное наугад в данном интервале, обладает весьма примечательным свойством: оно одновременно находится внутри каждого из вычислявшихся по ходу дела интервалов!
Именно это позволяет восстановить исходный текст, если мы знаем распределение вероятностей закодированных символов. Судите сами: делим единичный отрезок пропорционально вероятностям символов и находим, в какой интервал попадает кодовое число. Он и укажет, каков первый символ. Пропорционально делим интервал для найденного символа и опять смотрим, какому символу принадлежит интервал, где оказалось кодовое число. И так далее.
Я уже напоминал об идее алгоритма, но у него есть неожиданное свойство, не до конца укладывающееся в описанную логику. Вы помните: чем уже интервал, тем больше битов требуется... Так вот, если кодовое число внутри интервала выбирать не наугад, а с большим разбором, можно просто невероятно поднять эффективную степень сжатия. Фокус в том, что для записи числа, находящегося внутри даже очень узкого интервала, может потребоваться гораздо меньше битов, чем для представления границ интервала. Если, конечно, повезет найти соответствующее число.
Самый эффектный тому пример - число 0.5, которое, с одной стороны, кодируется всего одним битом, а с другой - может находиться в пределах невероятно узкого интервала, для записи границ которого нужны тысячи или миллионы битов...
Евгений Щербатюк
Компьютерная газета. Статья была опубликована в номере 07 за 2000 год в рубрике разное :: мелочи жизни


