Немного о сжатии информации
Как же так? Как возможно взять, скажем, текст, сжать его, чтобы он стал занимать в четыре раза меньше места, а потом восстановить в первозданном виде? А как же закон сохранения информации? Весь фокус в том, что любую информацию можно записывать бесконечно разными способами. Вот только одни из них являются более экономичными, чем другие. При перезаписи данных более экономным способом количество информации не уменьшается, она просто, так сказать, плотнее упаковывается. Чтобы получить о процессе "упаковки" информации более ясное представление, рассмотрим принципы работы нескольких популярных алгоритмов сжатия данных.
Самый примитивный из методов сжатия состоит в исключении повторяющихся символов или, если хотите, чисел. (Для обсуждения алгоритмов символы, впрочем, удобнее.) Этот метод не имеет самостоятельного значения, но все же используется иногда в графических форматах данных, где часто встречаются длинные последовательности точек одного цвета. Применив запись с повторителями, строку символов "ААБББВВВВ" можно превратить в "2А3Б4В". Выигрыш есть, но небольшой: текст стал короче на треть. Среди современных методов сжатия можно выделить две большие группы: в одних используются статистические техники, а в других - подстановки. Для начала познакомимся со статистическими методами.
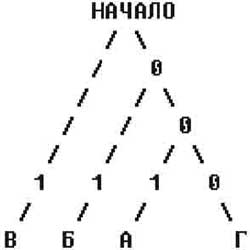
Алгоритм, изобретенный Хаффманом, является оптимальным, когда относительные частоты, с которыми встречаются символы, кратны степеням двойки. В первую очередь строится двоичное дерево, которое будет использоваться для перекодирования исходного текста. Пусть нам требуется сжать строку "ААБББВВВВГ". Для начала выпишем все встречающиеся в тексте символы в порядке убывания частоты их появления: "ВБАГ". Потом чисто механически выстроим над ними двоичное дерево, как это показано на рисунке 1.

Раскодировать сжатый текст просто: нужно читать полученный код бит за битом и идти по дереву от начала в направлении, задаваемом нулями или единицами, пока не найдешь первый символ. Когда символ найден, поиск следующего опять начинается от начала дерева. Для нашего примера последовательность битов "001" приводит к "А". Следом идет "001" - еще раз "А", а потом "01", то есть "Б" и так далее.
Строго говоря, способов построить дерево много, главное, чтобы соблюдалось правило: к символу, встречающемуся чаще других, должен вести более краткий путь. Если это правило соблюдается, то степень сжатия информации не зависит от вида конкретного дерева. Среди множества возможных деревьев есть такие, которые можно очень экономно запрограммировать. Эта техника и применяется во многих архиваторах, например, pkzip, lha, zoo, arj...
Очень похож на алгоритм Хаффмана алгоритм Шеннон-Фэно. Разница заключается в том, как строится дерево, то есть, как находится битовый код того или иного символа. Предположим, у нас есть вероятности (число повторов символа/длину текста) для каждого из возможных символов. Разделим множество всех символов на две части так, чтобы суммарная вероятность для всех символов в каждой из частей была одинаковой. Первый бит кода символа, принадлежащего одной или другой части, будет равен либо 0, либо 1. Описанная процедура деления полученных частей на подмножества повторяется для каждой из них до тех пор, пока в каждом из них не останется в точности по одному символу.
Если у вас сложилось впечатление, что алгоритм Хаффмана или Шеннона-Фэно совершенный, то это не так. Как уже упоминалось, эти способы кодирования оптимальны только в случаях, когда вероятности отдельных символов являются целыми степенями 1/2. А так практически никогда не бывает. Указанное ограничение преодолено в методе арифметического кодирования, предложенном Илиасом. С его помощью практически достигается теоретически возможный предел сжатия данных, положенный законом сохранения информации.
При арифметическом кодировании вычисляется число в интервале от 0 до 1. По мере роста числа обработанных символов интервал становится уже и уже, а для записи числа требуется все большее количество битов. Каждый последующий символ уменьшает интервал на величину, обратно пропорциональную вероятности символа. Чем больше вероятность, тем меньше убывание интервала, тем меньше битов добавляется к итоговому числу.
Чтобы стало ясно, о чем идет речь, давайте рассмотрим пример кодирования текста "АБА", состоящего из двух символов: "А" и "Б". Их вероятности равны 2/3 и 1/3 соответственно. Итак, первоначальный интервал равен 0-1. Если первым в тексте идет символ "А", то интервал станет 0-2/3, а если Б, то 2/3-1. Если вторым символом идет "А", то для получения нового интервала нужно взять "нижние" 2/3 от предыдущего. То есть для последовательностей "АА" и "БА" интервалы будут равны 0-4/9 и 2/3-8/9 соответственно.
Аналогичным образом, если вторым символом текста будет не "А", а символ "Б", то для получения нового интервала нужно взять "верхнюю" 1/3 от предыдущего. В таком случае интервалы для последовательностей "АБ" и "ББ" будут равны 4/9-2/3 и 8/9-1 соответственно. Процедура вычисления интервала продолжается в соответствии с описанной схемой до тех пор, пока не будет прочитан последний символ кодируемого текста.
Собственно результатом кодирования является число, которое с некоторой степенью условности можно назвать вероятностью. Это число выбирается так, чтобы оно находилось внутри вычисленного интервала и, по возможности, записывалось минимальным числом битов. Для нашего примера (текст "АБА") результирующий интервал 4/9-16/27, а на роль результирующего числа идеально подходит 4/8, то есть 0,1 в двоичной записи. Ноль и запятую можно отбросить: мы и так знаем, что кодовое число дробное. Взгляните - мы сжали 24-битовый текст до всего-навсего одного бита!
Сжать-то сжали, но как его восстановить? Из одного бита? Это возможно, если известны вероятности для входивших в исходный текст символов. Напомню: для "А" вероятность 2/3 а для "Б" - 1/3. Руководствуясь совершенно такой же логикой, как при кодировании, сначала мы должны вычислить возможные интервалы для первого символа: для "А" 0-2/3, для "Б" 2/3-1. Наш код, равный 1/2, попадает в интервал для "А", значит, это и есть первый искомый символ.
Теперь вычислим возможные интервалы для случаев разных вторых символов: для "А" 0-4/9, для "Б" 4/9-2/3. На сей раз код попадает в интервал для "Б". Это и есть второй символ. Продолжая описанную процедуру, мы сможем восстановить весь исходный текст. Нужно только знать, когда остановиться, то есть должно быть заранее известно общее число символов в исходном тексте.
Итак, алгоритмы сжатия данных у нас есть. Дело за тем, чтобы эффективно их запрограммировать. В первую очередь нужно разобраться с вероятностями появления символов в исходном тексте. Очевидно, что их можно хранить в таблице (массиве) размером в 256 строк, по строке на каждый из возможных символов. Если, конечно, считать, что каждый байт - символ.
Сразу можно сказать, что формирование таблицы вероятностей символов путем предварительного прочтения всего исходного текста и последующих вычислений является самым медленным способом из всех возможных. Правда, он сулит максимальную степень сжатия. Нужно искать компромисс.
Одно из возможных решений такое, что готовится несколько стандартных таблиц, пригодных на все случаи жизни. Одна таблица для текстовых файлов, другая - для программ, третья - для картинок и так далее. Естественно, использование обобщенных таблиц снижает возможную степень сжатия, но у них есть одно интересное преимущество. Дело в том, что стандартные таблицы можно встроить непосредственно в программу-архиватор, вместо того, чтобы включать их в состав сжатого файла на правах служебной информации.
Другой способ, устраняющий необходимость предварительного прочтения сжимаемого текста, называется адаптивным. Одна из реализаций адаптивного метода начинает работу исходя из предположения, что все символы появляются с одинаковой частотой. По мере прочтения и кодирования символов накапливаются сведения о частоте их появления и таблица кодировки постоянно уточняется. То есть по мере кодирования степень сжатия данных возрастает.
Другая реализация адаптивного метода, считающаяся лучшей из известных в настоящее время, основана на применении динамического кодирования по Маркову. Наиболее эффективные современные программы-архиваторы используют алгоритм арифметического сжатия данных в сочетании с одним из адаптивных методов построения таблицы вероятностей.
Если статистические алгоритмы сжатия так хороши, то почему же их не используют повсеместно? Во-первых, эти алгоритмы являются сравнительно новыми и, возможно, просто еще не успели захватить рынок. А во-вторых, и это важнее, для их работы требуются значительные ресурсы, то есть мощный процессор и большой объем оперативной памяти. Иными словами, они работают медленно, и этот проигрыш не всегда окупается сравнительно небольшим увеличением степени сжатия.
Внимательный читатель немедленно спросит: "сравнительно небольшое увеличение по сравнению с чем?" По сравнению со сжатием, которое достигается применением класса алгоритмов, которые используют технику подстановок. Для этих алгоритмов есть и другое название: "основанные на словарях". Но об этом мы поговорим в следующий раз.
Евгений Щербатюк
Компьютерная газета. Статья была опубликована в номере 03 за 2000 год в рубрике разное :: страна советов


